(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5,whereM is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be 14MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.
Video Solution
Text Solution
Given moment of inertia of a sphere about a diameter IAB=25MR2
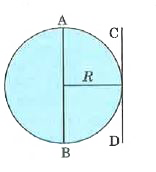
To find moment of inertia of the sphere about a tangent CD, we use parallel axes theorem.
∴ Moment of inertia of the sphere about the tangent CD is given by
IT=IAB+MR2=25MR2+MR2
IT=75MR2
(b) Given moment of inertia of circular dise about diameter,
Id=14MR2
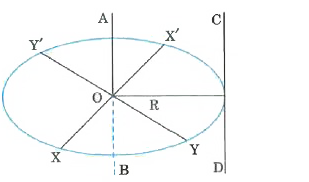
To find the moment of inertia of the disc about an axis normal to the disc eand passing through the centre, we use perpendicular axis theorem.
Id= moment of inertia about any of the two dimaeters XX and YY
Using perpendicular axis theorem,
MI of the disc about AB,
IAB=Id+Id=14MR2+14MR2
IAB=12MR2
To find MI of the disc about a tangent perpendicular to its plane and passing through a point on its edge, we use parallel axis theorem
IT=IAB+MR2
IT=12MR2+MR2=32MR2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )12videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))13videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS TOUGH & TRICKY8videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
AMR22BMR24CMR23DMR212 - Question 2 - Select One
The moment of inertia of a thin circular disc of mass M and radius R about any diameter is
AMR24BMR22CMR2D2MR2 - Question 3 - Select One
The moment of inertia of a thin circular disc of mass M and radius R about any diameter is
AMR24BMR22CMR2D2MR2
Moment of inertia of a circular wire of mass M and radius R about its diameter is
View SolutionMoment of inertia of a circular wire of mass M and radius R about its diameter is :
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionThe moment of inertia of a solid sphere of density p and radius R about its diameter is
View SolutionThe moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
View Solution

