A flat car of mass M is at rest on a frictionless floor with a child of mass m standing at its edge. If the child jumps off from the car towards right with an initial velocity u, with respect to the car, find the velocity of the car after its jump.
To solve the problem, we will use the principle of conservation of momentum. Here are the steps to find the velocity of the car after the child jumps off:
1. Identify the system and its initial conditions:
- We have a flat car of mass M at rest on a frictionless floor.
- A child of mass m is standing at the edge of the car.
- Both the car and the child are initially at rest, so the initial momentum of the system is zero.
2. Define the final conditions after the child jumps:
- The child jumps off the car with a velocity u relative to the car towards the right.
- Let the velocity of the car after the jump be V (to the left).
3. Apply the conservation of momentum:
- According to the conservation of momentum, the total momentum before the jump must equal the total momentum after the jump.
- Initial momentum of the system:
Pinitial=0
- Final momentum of the system:
- The momentum of the child after jumping (with respect to the ground) is:
Pchild=m(u+V)
Here, V is negative because the car moves to the left.
- The momentum of the car after the jump is:
Pcar=−MV
- Therefore, the total final momentum is:
Pfinal=−MV+m(u+V)
4. Set the initial momentum equal to the final momentum:
0=−MV+m(u+V)
5. Rearranging the equation:
MV=m(u+V)
Expanding this gives:
MV=mu+mV
Rearranging terms:
MV−mV=mu
Factoring out V:
V(M−m)=mu
6. Solve for the velocity of the car V:
V=muM+m
Final Answer:
The velocity of the car after the child jumps off is:
V=muM+m
- We have a flat car of mass M at rest on a frictionless floor.
- A child of mass m is standing at the edge of the car.
- Both the car and the child are initially at rest, so the initial momentum of the system is zero.
- The child jumps off the car with a velocity u relative to the car towards the right.
- Let the velocity of the car after the jump be V (to the left).
- According to the conservation of momentum, the total momentum before the jump must equal the total momentum after the jump.
- Initial momentum of the system:
Pinitial=0
- Final momentum of the system:
- The momentum of the child after jumping (with respect to the ground) is:
Pchild=m(u+V)
Here, V is negative because the car moves to the left.
- The momentum of the car after the jump is:
Pcar=−MV
- Therefore, the total final momentum is:
Pfinal=−MV+m(u+V)
0=−MV+m(u+V)
MV=m(u+V)
Expanding this gives:
MV=mu+mV
Rearranging terms:
MV−mV=mu
Factoring out V:
V(M−m)=mu
V=muM+m
The velocity of the car after the child jumps off is:
V=muM+m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
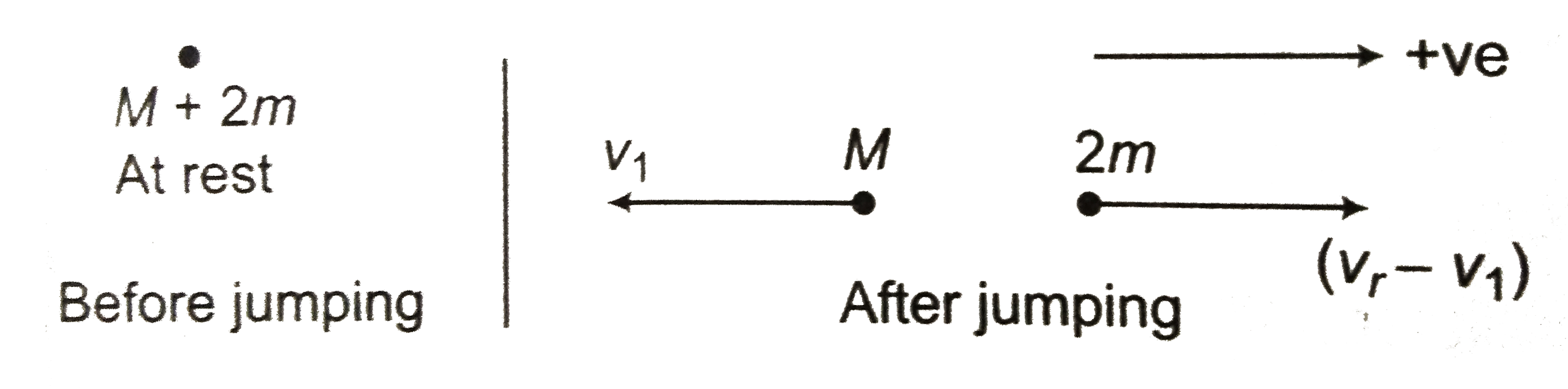
A trolley of mass M is at rest over a smooth horizontal surface as shown in figure. Two boys each of mass 'm' are standing over the trolley. They jump from the trolley (towards right) with relative velocity vr [relative to velocity of trolley just after jumping]
(a) together
(b) one after the other.
Find velocity of trolley in both cases.
View SolutionA man of mass m stands on a long flat car of mass M , moving with velocity V.If he now begins to run with velocity u, with respect to the car , in the same direction as V, the the velocity of the car will be
View SolutionA rail road car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man aproaching the engine?
View Solution
A child with mass m is standing at the edge of a merry go round having moment of inertia I, radius R and initial angular velocity ω as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity v with respect to the ground. The new angular velocity of the merry go round is
View SolutionA car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in the figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100 m/s with respect to the car at an angle 30∘ with the horizontal.

The first cannon ball hits the stationary carriage after a time t0 and sticks to it. Determine t0. (in sec)
View SolutionTwo persns each of mass m are standing at the two extremes of a railroad car of mas M resting on a smooth track figure. The person on left jumps to the left with a horizontal speed u with respect to the state f the cr before the jump. Threafter, the other person jumps to the right, again with the same horizontl speed u with respect to teg state of the car before his jump. Find the vellcity of the car after both the person hae jumped off.

View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View SolutionA girl of mass 50 kg stands on a railroad car of mass 75 kg moving with velocity 20ms−1 . Now , the girl begins to run with a velocity of 10ms−1 with respect to the car in the same direction , as that of the car. The velocity of the car at this instant will be
View SolutionA plank of mass 2m and length L is al rest on a frictionless horizontal floor At one end of it, a child of mass m is standing as shown in figure If child walks and reaches the other and then the distance travelled by child wrt ground will be
View SolutionA child of mass m is standing, on the periphery of a circular platform of radius R, which can rotate about its central axis. The moment of inertia of the platform is I. Child jumps off from the platform with a velocity u tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.
View Solution
