A force of −4FˆK acts O, the origin of the coordinate system. The torque about the point (1,−1) is
Torque, τ=r×F=[(1−0)ˆi+(−1−0)ˆj+(0−0)ˆk]×(−10)ˆk=10(ˆi−ˆj)×(−ˆk)=10(ˆi+ˆj)Nm
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
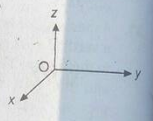 AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
 AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)A force of −Fˆk actgs on O, the origin of the coodinate system. The torque about the point (1,-1) is
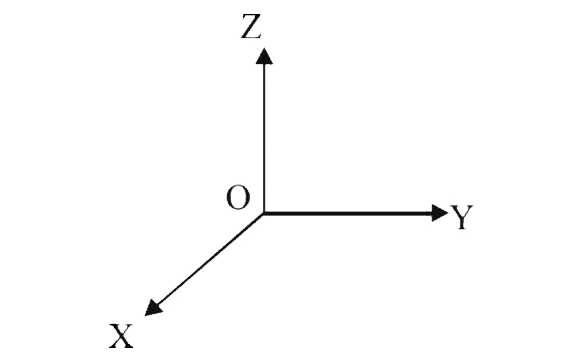 AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
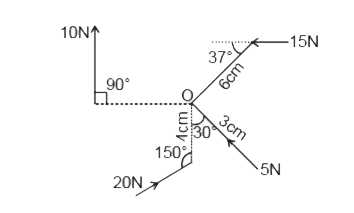
Calculate the total torque acting on the body shown in figure about the point O
View SolutionA force of −Fˆk on O, the origin of the coordinate system. The torque about the point (1,−1) is.
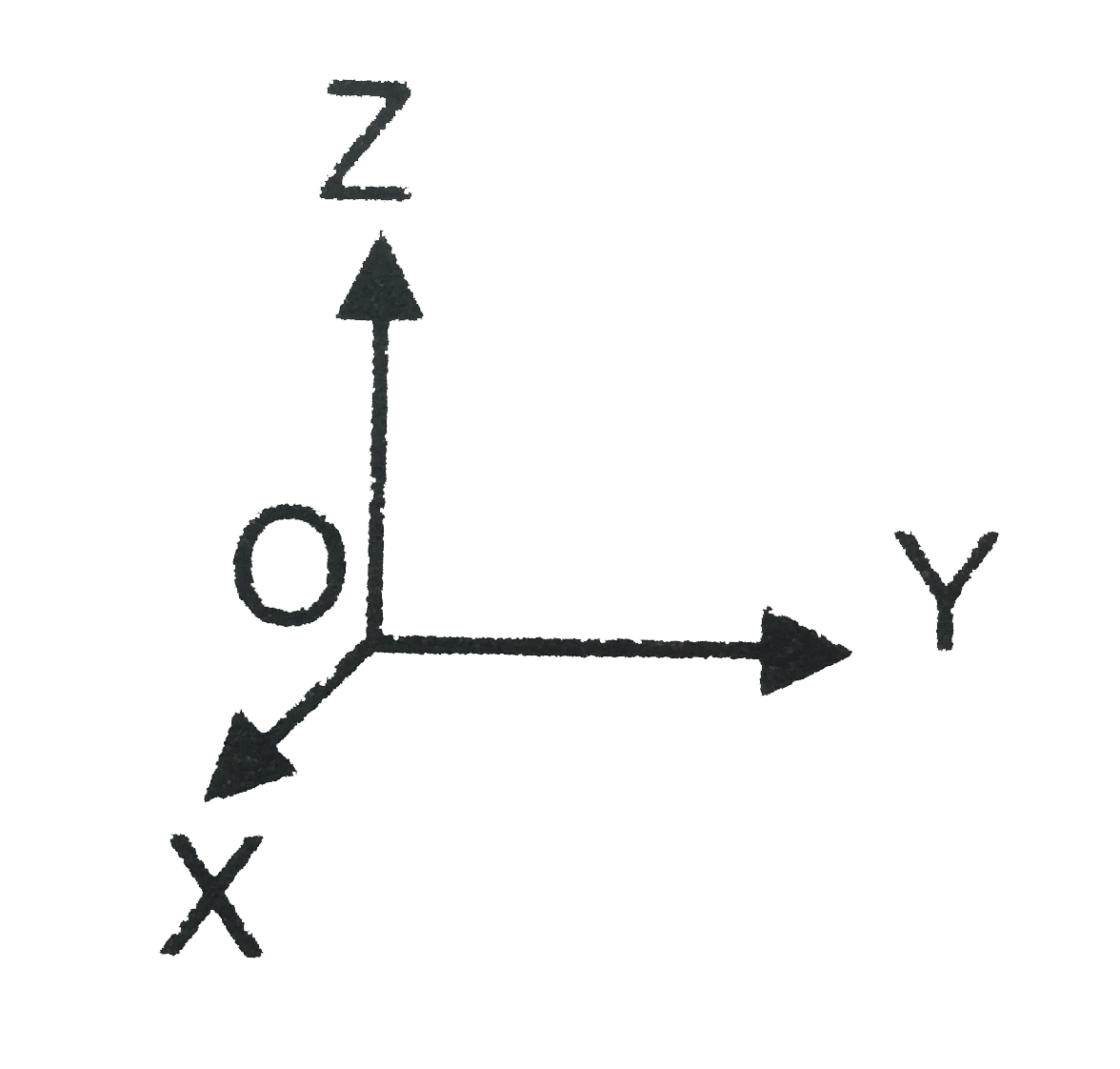 .
.
View SolutionA force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
View SolutionA particle is placed at the origin of the coordinate system. Two forces of magnitude 20N&10N act on it as shown in figure. It is found that it starts moving towards the point (1,1) . The net unknown force acting on the particle at this position can be :
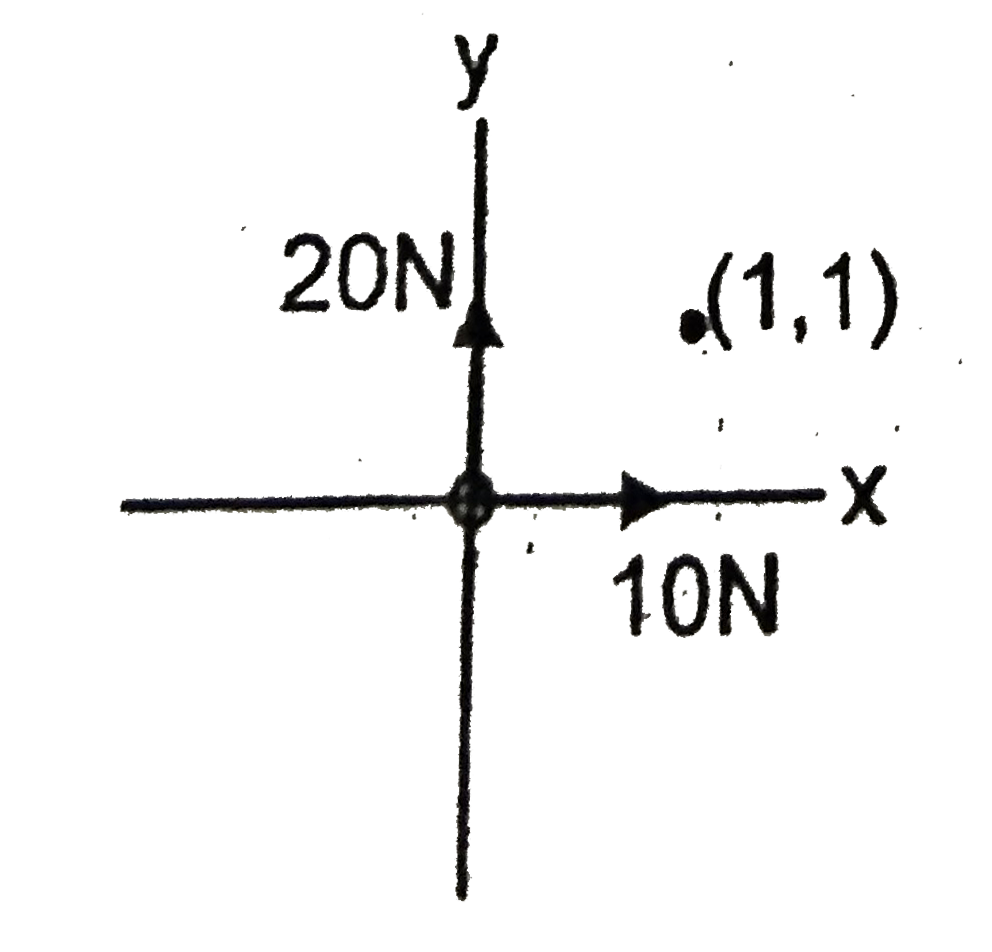
View SolutionStatement-I : Magnitude of torque of a force about a given point does not depend upon the location of the origin of the co-ordinate system.
Statement II: Moment of couple is different for different points in its plane
View Solution
