A single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
In the negative z-direction
In the positive z-direction
In the positive y-direction
In the negative y-direction
To determine the direction of the force acting on a particle situated on the negative x-axis, given that the torque about the origin is in the positive z-direction, we can follow these steps:
1. Identify the Position Vector:
The particle is located on the negative x-axis. Let's denote its position vector as:
r=−r^i
where r is the distance from the origin to the particle.
2. Understand Torque Direction:
The torque (τ) is given to be in the positive z-direction. In vector notation, this can be expressed as:
τ=τ^k
where τ is a positive scalar.
3. Use the Torque Equation:
The torque is defined as the cross product of the position vector and the force vector:
τ=r×F
Substituting the position vector:
τ=(−r^i)×F
4. Express the Force Vector:
Let the force vector be represented as:
F=Fx^i+Fy^j+Fz^k
5. Calculate the Cross Product:
Now, we compute the cross product:
τ=(−r^i)×(Fx^i+Fy^j+Fz^k)
Using the properties of the cross product, we have:
τ=−r(^i×Fx^i+^i×Fy^j+^i×Fz^k)
Since ^i×^i=0, we can simplify this to:
τ=−r(0+Fy^k−Fz^j)=−rFz^j+rFy^k
6. Set Torque Direction:
For the torque to be in the positive z-direction, we need:
−rFz=0(no component in the j direction)
rFy=τ>0(positive component in the k direction)
This implies Fz=0 and Fy>0.
7. Determine the Force Direction:
Since Fy>0 and Fz=0, the force must be directed in the positive y-direction. However, we also need to consider the overall direction of the force. The force must be in the negative y-direction to produce a positive torque about the origin.
Conclusion:
The force acting on the particle situated on the negative x-axis, which produces a torque in the positive z-direction, must be directed in the negative y-direction.
The particle is located on the negative x-axis. Let's denote its position vector as:
r=−r^i
where r is the distance from the origin to the particle.
The torque (τ) is given to be in the positive z-direction. In vector notation, this can be expressed as:
τ=τ^k
where τ is a positive scalar.
The torque is defined as the cross product of the position vector and the force vector:
τ=r×F
Substituting the position vector:
τ=(−r^i)×F
Let the force vector be represented as:
F=Fx^i+Fy^j+Fz^k
Now, we compute the cross product:
τ=(−r^i)×(Fx^i+Fy^j+Fz^k)
Using the properties of the cross product, we have:
τ=−r(^i×Fx^i+^i×Fy^j+^i×Fz^k)
Since ^i×^i=0, we can simplify this to:
τ=−r(0+Fy^k−Fz^j)=−rFz^j+rFy^k
For the torque to be in the positive z-direction, we need:
−rFz=0(no component in the j direction)
rFy=τ>0(positive component in the k direction)
This implies Fz=0 and Fy>0.
Since Fy>0 and Fz=0, the force must be directed in the positive y-direction. However, we also need to consider the overall direction of the force. The force must be in the negative y-direction to produce a positive torque about the origin.
The force acting on the particle situated on the negative x-axis, which produces a torque in the positive z-direction, must be directed in the negative y-direction.
Topper's Solved these Questions
Similar Questions
A force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle.
View SolutionThe position vector →r of a particle points along the positive direction of a z axis. If the torque on the particle is (a) zero, (b) in the negative direction of x, and ( c) in the negative direction of y, in what direction is the force causing the torque?
View Solution
Knowledge Check
A conservative force acts on a particle as the particle moves along the positive x-axis from origin origin to x=2m. The force is parallel to x-axis. Now, consider four different cases, as shown in the figures, 1, 2, 3, and 4, where the forces is shown as a function of x. Rank the situations according to the change in potential energy associated with the force, least ( or most negative) to greatest ( or most positive).
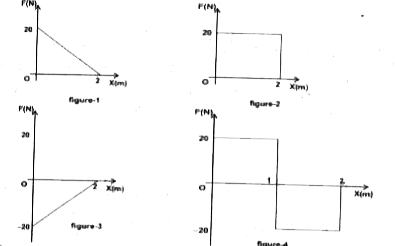 A2, 1, 4, 3B3, 4, 1, 2C1, 2, 3, 4D4, 2, 3, 1
A2, 1, 4, 3B3, 4, 1, 2C1, 2, 3, 4D4, 2, 3, 1If is the force acting on a particle having position vector and be the torque of this force about the origin, then-
A→r.→τ and →F.→τ≠0B→r.→τ and →F.→τ=0C→r.→τ>0 and →F.→τ<0D→r.→τ=0 and →F.→τ=0A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
 AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)
A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is

View SolutionA force of −4FˆK acts O, the origin of the coordinate system. The torque about the point (1,−1) is
View SolutionA force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
View SolutionLet →F be the force acitng on a paritcle having positon vector →rand→T be the torque of this force about the origin. Then
View SolutionLet →F be the force acitng on a paritcle having positon vector →rand→T be the torque of this force about the origin. Then
View Solution
