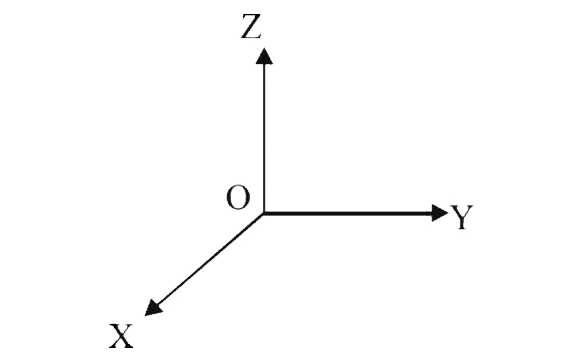
A force of −Fˆk actgs on O, the origin of the coodinate system. The torque about the point (1,-1) is
F(ˆi−ˆj)
−F(ˆi+ˆj)
F(ˆi+ˆj)
−F(ˆi−ˆj)
The correct Answer is:B
(b) Torque →τ=→r×→F=(ˆj−ˆi)×(Fˆk)=−F(ˆi+ˆj)
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Knowledge Check
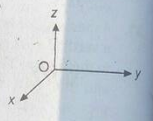
A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)A force of −F,ˆk acts on O, the origin of the coordinate system. The torque about the point (1,-1) is
AF(ˆi−ˆj)B−F(ˆi+ˆj)CF(ˆi+ˆj)D−F(ˆi−ˆj)A force of −4FˆK acts O, the origin of the coordinate system. The torque about the point (1,−1) is
A−4F(ˆi−ˆj)B4F(ˆi−ˆj)C−4F(ˆi+ˆj)D4F(ˆi+ˆj)
Let a force F be acting on a body free to rotate about a point O and let r be the position vector of any point P on the line of action of the force. Then torque (τ) of this force about point O is defined as τ=r×F Given, F=(2ˆi+3ˆj−ˆk)Nandr=(ˆi−ˆj+6ˆk)m. Find the torque of this force.
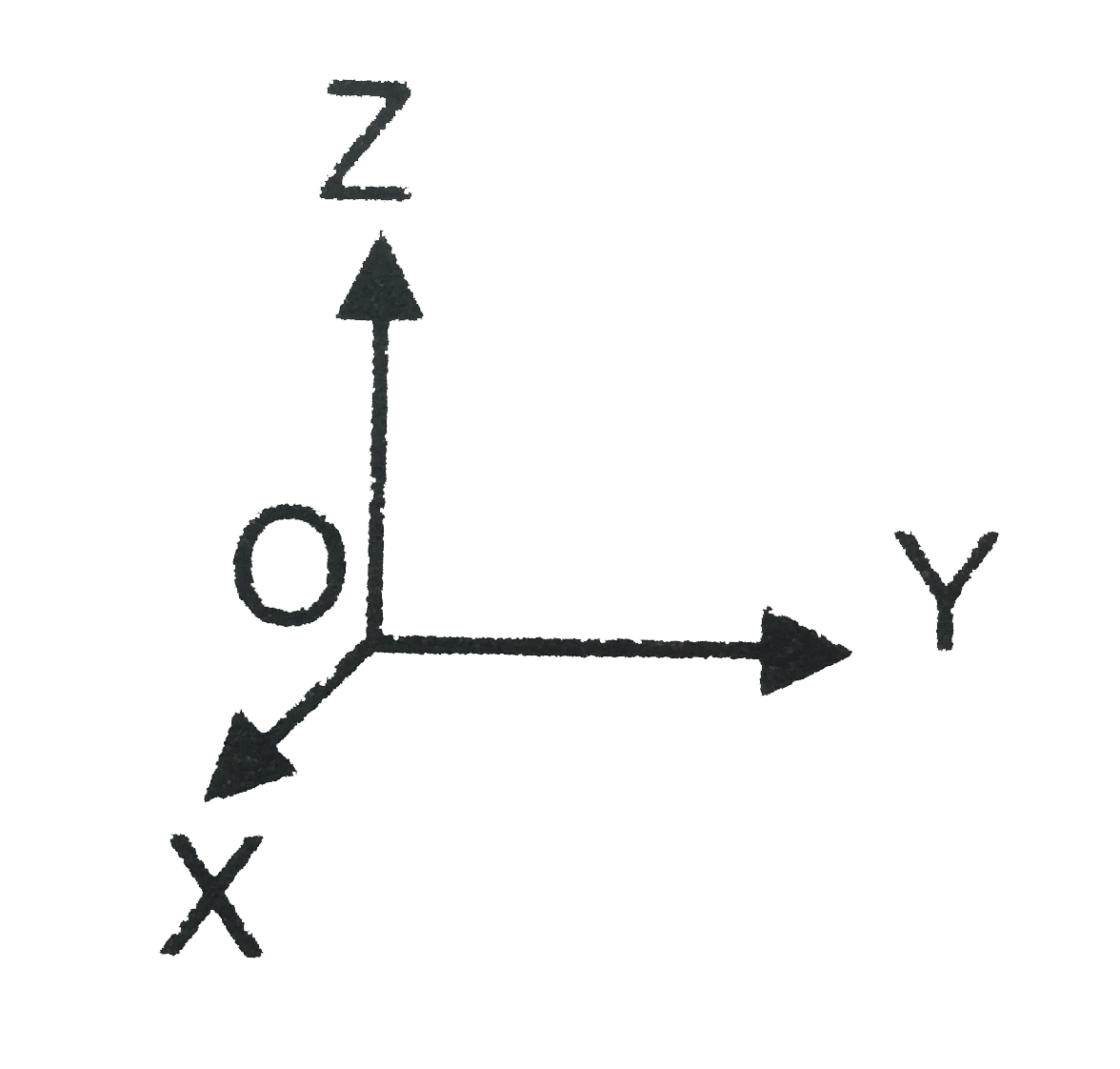
View SolutionA force of −Fˆk on O, the origin of the coordinate system. The torque about the point (1,−1) is.
.
View SolutionA force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
View SolutionStatement-I : Magnitude of torque of a force about a given point does not depend upon the location of the origin of the co-ordinate system.
Statement II: Moment of couple is different for different points in its plane
View SolutionA force F=2ˆi+3ˆj−ˆk acts at a point (2,-3,1). Then magnitude of torque about point (0,0,2) will be
View Solution