A galvanometer of resistance is to be converted into an ammeter, with the help of a shunt of resistance R. If the ratio of the heat dissipated through galvanometer and shunt is 3:4, then
The correct Answer is:A
To solve the problem, we need to find the relationship between the resistance of the galvanometer RG and the shunt resistance R given that the ratio of heat dissipated through the galvanometer and the shunt is 3:4.
1. Understanding the Heat Dissipation Formula:
The heat dissipated in a resistor can be expressed using the formula:
H=V2R⋅t
where H is the heat dissipated, V is the potential difference across the resistor, R is the resistance, and t is the time.
2. Heat Dissipated in the Galvanometer:
For the galvanometer, the heat dissipated HG can be written as:
HG=V2RG⋅t
3. Heat Dissipated in the Shunt:
For the shunt, the heat dissipated HS can be written as:
HS=V2R⋅t
4. Setting Up the Ratio:
According to the problem, the ratio of the heat dissipated through the galvanometer to that through the shunt is given as:
HGHS=34
5. Substituting the Heat Expressions:
Substitute the expressions for HG and HS into the ratio:
V2RG⋅tV2R⋅t=34
6. Simplifying the Ratio:
The V2 and t terms cancel out:
1RG⋅R=34
7. Rearranging the Equation:
Rearranging gives us:
R=34RG
8. Finding the Relationship:
To express RG in terms of R:
RG=43R
Conclusion:
Thus, the relationship between the shunt resistance R and the galvanometer resistance RG is:
RG=43R
The heat dissipated in a resistor can be expressed using the formula:
H=V2R⋅t
where H is the heat dissipated, V is the potential difference across the resistor, R is the resistance, and t is the time.
For the galvanometer, the heat dissipated HG can be written as:
HG=V2RG⋅t
For the shunt, the heat dissipated HS can be written as:
HS=V2R⋅t
According to the problem, the ratio of the heat dissipated through the galvanometer to that through the shunt is given as:
HGHS=34
Substitute the expressions for HG and HS into the ratio:
V2RG⋅tV2R⋅t=34
The V2 and t terms cancel out:
1RG⋅R=34
Rearranging gives us:
R=34RG
To express RG in terms of R:
RG=43R
Thus, the relationship between the shunt resistance R and the galvanometer resistance RG is:
RG=43R
Topper's Solved these Questions
Similar Questions
Knowledge Check
A galvanometer of resistance 70Ω, is converted to an ammeter by a shunt resistance r3=0.03Ω. The value of its resistance will become
A0.025ΩB0.022ΩC0.035ΩD0.030Ω
A moving coil galvnometer is converted into an ammeter reading up to 0.03A by connecting a shunt of resistance r4. What is the maximum current which can be sent through this galvanometer if no shunt is used (here r=resistance of galvanometer)
View SolutionA galvanometer of resistance 50Ω is converted into an ammeter by connecting a low resistance (shunt) of value 1Ω in parallel to the galvanometer, S. If full - scale deflection current of the galvanometer is 10 mA, then the maximum current that can be measured by the ammeter is -
View SolutionA galvanometer has resistance 36Ω if a shunt of 4Ω is added with this, then fraction of current that passes through galvanometer is:
View SolutionA moving coil galvanometer is converted into an ammeter reads upto 0.03A by connecting a shunt of resistance 4r across it and ammeter reads up 0.06A, when a shunt of resistance r is used. What is the maximum current which can be sent through this galvanometer if no shunt is used ?
View Solution(A) : If a galvanometer is converted into an ammeter and a milliammeter then the shunt resistance of ammeter is lower than that of milliammeter.
(R) : In Ammeter the current through shunt is less than that of galvonameter as compared to the case of milliammeter.
View SolutionIn Q.36, the combined resistance of the shunt and the galvanometer is
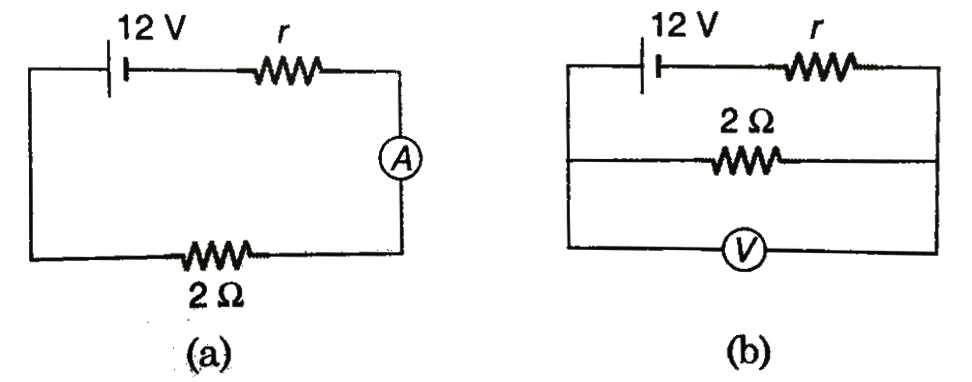
View SolutionA galvanometer (coil resistance 99Ω.) is converted into an ammeter using a shunt of 1Ω and connected as shown in figure (a). The ammeter reads 3A. The same galvanometer is convened into a voltmeter by connecting a resistance of 101Ω in series. This voltmeter is connected at, shown in figure (b). Its reading is found to be 45 of the full scale reading. Find :
(a) internal resistance r of the cell
(b) range of the ammeter and voltmeter
(c) full scale deflection current of the galvanometer.
View Solution
