A gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).
We neglect the moment of inertia of the gas in a shell. Then the moment of friction forces on a unit length of the cylinder must be a constant as a function of r.
So, 2πr3ηdωdr=N1 or ω(r)=N14πη(1r21−1r2)
and ω=N14πη(1r21−1r22) or η=N14πω(1r21−1r22).
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations
35 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A fluid with viscosity η fills the space between two long co-axial cylinders of radii R1and R2, with R1<R2. The inner cylinder is stationary while the outer one is rotated with a constant angular velocity ω2. The fluid flow is laminar. Taking into account that the friction force acting on a unit area of a cylindrical surface of radius r is defined by the formula σ=ηr(∂ω/∂r), find:
(a) the angular velocity of the rotating fluid is as a function of radius r,
(b) the moment of the friction forces acting on a unit length of the outer cylinder.
View SolutionUnder standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?
View Solution
Knowledge Check
In the above question, the frictional force on the cylinder is
AF/3 towards rightBF/3 towards leftC2F/3 towards rightD2F/3 towards leftIn the question number 89, the force of friction acting on the cylinder is
A2/3 Mg sinθB1/3 Mg sinθC2/5 Mg sinθD2/7 Mg sinθA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
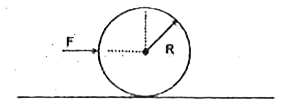 Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained
Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained
Find the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
View SolutionA uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?

View SolutionFind the temperature distribution in the space between two coaxial cylinders of radii R1 and R2 filled with a uniform heat conducting substance if the temperatures of the cylinders are constant and are equal to T1 and T2 respectively.
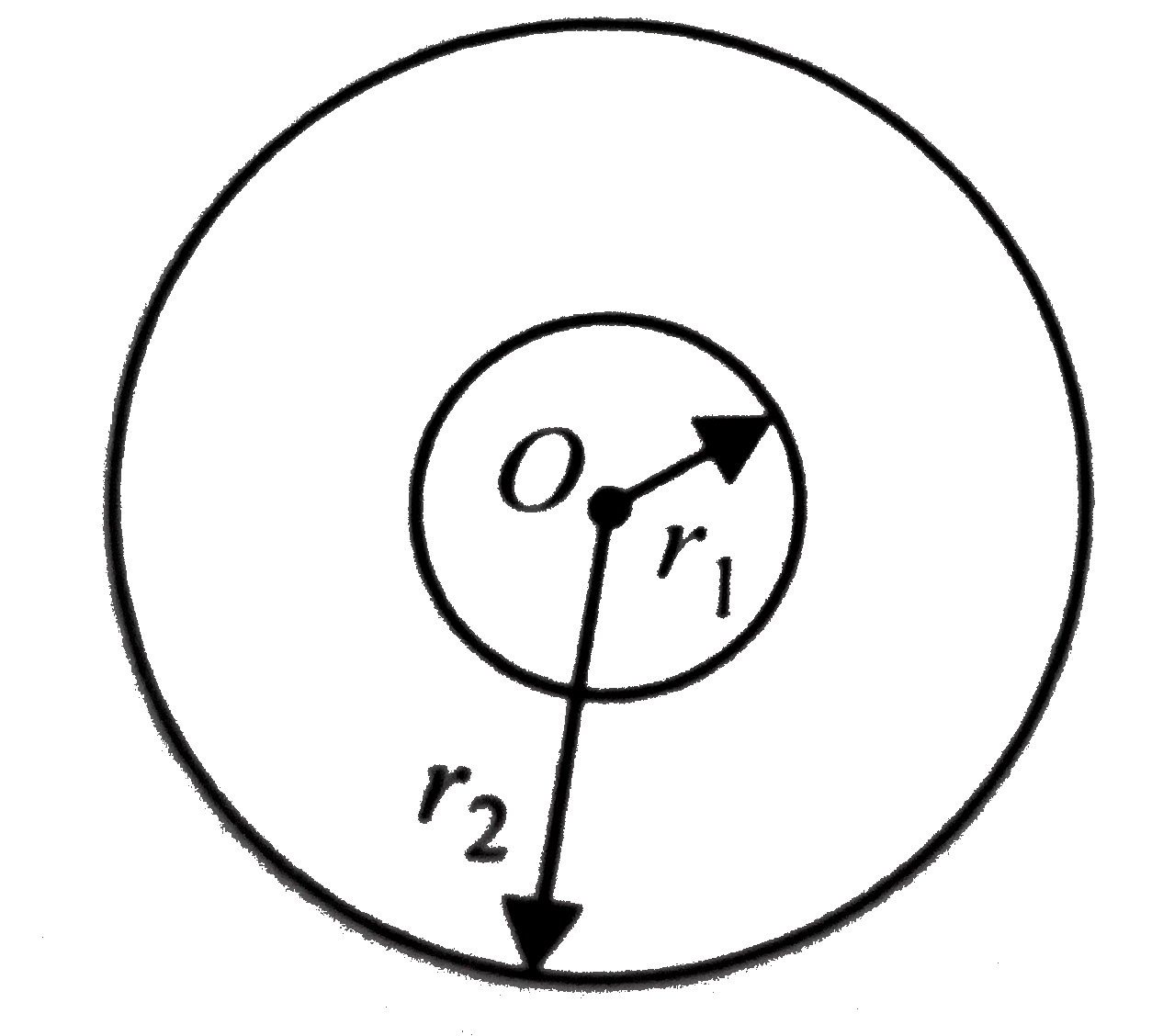
View SolutionSpace between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
View SolutionA cylinder rolls up an inclined plane, reaches someheight and then rolls down (without slipping throught these motions). The direction of the frictional force acting on the cylinder are -
View Solution
