A glass tumbler having irmer depth of 17.5 cm is kept on a table. A student starts pouring water ( =4/3) into it while looking at the surface of water from the above. When he feels that the tumbler is half filled, he stops pouring water. Up to what height, the tumbler is actually filled ?
10 cm
11.7 cm
7.5 cm
8.75 cm
To solve the problem, we need to determine the actual height of water in the tumbler when the student perceives it to be half-filled. We will use the concept of apparent depth due to refraction.
1. Identify the given values:
- Inner depth of the tumbler, D=17.5cm
- Refractive index of water, μ=43
2. Determine the perceived height of water:
- The student perceives the tumbler to be half-filled. Therefore, the perceived height of water, h′, is:
h′=D2=17.5cm2=8.75cm
3. Relate the actual height of water to the perceived height:
- The actual height of water, h, can be related to the perceived height using the formula for apparent depth:
h′=hμ
- Substituting the values we have:
8.75=h43
4. Solve for the actual height h:
- Rearranging the equation gives:
h=8.75×43
- Calculating this:
h=8.75×43=353≈11.67cm
5. Conclusion:
- The actual height of water in the tumbler when the student perceives it to be half-filled is approximately 11.67cm.
Final Answer:
The tumbler is actually filled up to approximately 11.67 cm.
- Inner depth of the tumbler, D=17.5cm
- Refractive index of water, μ=43
- The student perceives the tumbler to be half-filled. Therefore, the perceived height of water, h′, is:
h′=D2=17.5cm2=8.75cm
- The actual height of water, h, can be related to the perceived height using the formula for apparent depth:
h′=hμ
- Substituting the values we have:
8.75=h43
- Rearranging the equation gives:
h=8.75×43
- Calculating this:
h=8.75×43=353≈11.67cm
- The actual height of water in the tumbler when the student perceives it to be half-filled is approximately 11.67cm.
The tumbler is actually filled up to approximately 11.67 cm.
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B20videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A)81videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS30videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS246videos
JEE MAINS 2020
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)10videos
JEE MAINS 2022
Similar Questions
A vessel having perfectly reflecting plane botton is filled with water (μ=4/3) to depth d. A point source of light is placed at a height h above the surface of water. Find the distance of final image from water surface.
View SolutionAn inverted cone has a depth of 10cm and a base of radius 5cm. Water is poured into it at the rate of 3/2 c.c. per minute. Find the rate at which the level of water in the cone is rising when the depth is 4cm.
View Solution
Knowledge Check
- Question 1 - Select One
A glass beaker of mass 400 kg floats in water with the open end just touching the surface of water and half of the beaker filled with water. The inner volume of the beaker is 500cm3 What is the density of the meterial of the beaker ?
A1.52gcm−3B2.67gcm−3C3.01gcm−3D3.87gcm−3 - Question 2 - Select One
Two equal glasses are respectively 13 and 14 full of milk they are then filled up with water and the content mixed in a tumbler the ratio of milk and water in the tumbler is
A7 : 5B7 : 17C3 : 7D11 : 23 - Question 3 - Select One
A mark is made on the bottom of a vessel and over this mark, a glass slab to thickness 3.5cm and refractive index 74 is placed. Now water (refractive index, 43) is poured into the vessel so that the surface of water is 8cm above the upper surface of the slab. Looking down of normally through the water, the apparent depth of the mark below the surface of water will be :
A6.33cmB7.5cmC8cmD10cm
Water leaks out from an open tank through a hole of area 2mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis 0.4m2. The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt.
d. From the result of part c. find the time required for half of the water to leak out.View SolutionHow much water (in cm) should be filled in a container of height 12 cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)
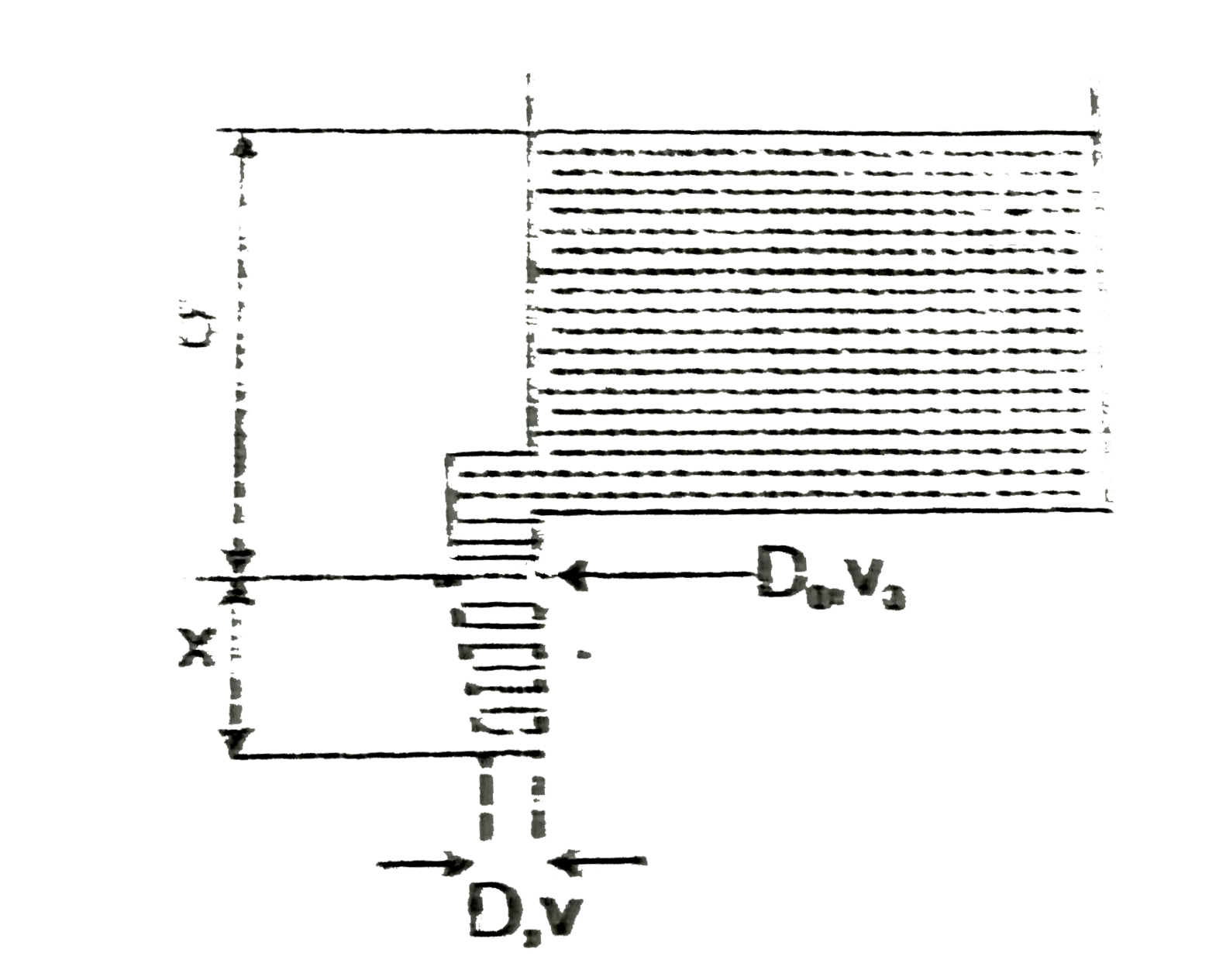
A student observes after setting up this experiment that for a tap with D0=1cm at x=0.3m the stream diameter D=0.9cm. The heights b of the water above the tap in this case will be:View SolutionA glass beaker is filled with water up to 5cm. It is kept on top of a 2cm thick glass slab. When a coin at the bottom of the glass slab is viewed at the normal incidence from above the beaker, its apparent depth from the water surface is dcm. Value of d is close (the refractive index of water and glass are 1.33 and 1.50,respectively)
View SolutionHow much water should be filled in a container of height 21cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
View Solution

