A graph of the square of the velocity against the square of the acceleration of a given simple harmonic motion is
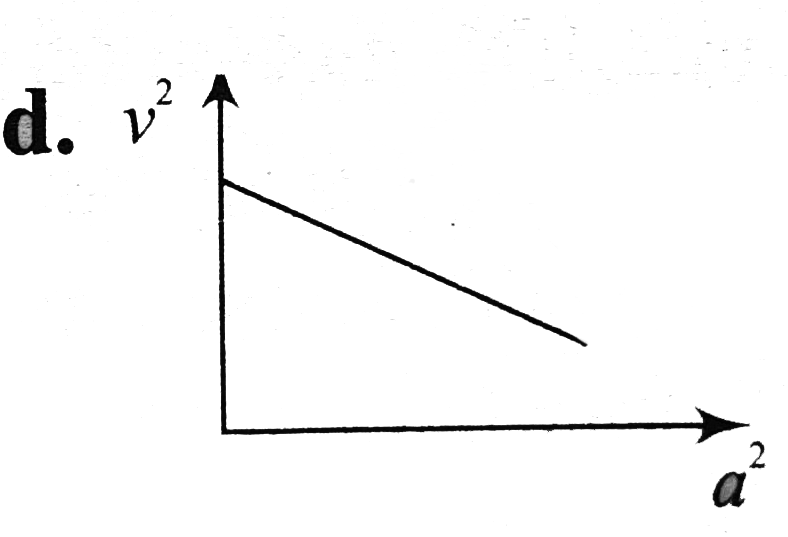
The correct Answer is:D
To solve the problem of determining the nature of the graph of the square of the velocity against the square of the acceleration in simple harmonic motion (SHM), we can follow these steps:
Step 1: Understand the equations of SHM
In simple harmonic motion, the displacement x can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
Step 2: Find the expression for velocity
The velocity v is the derivative of displacement with respect to time:
v=dxdt=Aωcos(ωt+ϕ)
Thus, the square of the velocity is:
v2=(Aωcos(ωt+ϕ))2=A2ω2cos2(ωt+ϕ)
Step 3: Find the expression for acceleration
The acceleration a is the derivative of velocity with respect to time:
a=dvdt=−Aω2sin(ωt+ϕ)
Thus, the square of the acceleration is:
a2=(−Aω2sin(ωt+ϕ))2=A2ω4sin2(ωt+ϕ)
Step 4: Relate v2 and a2
Now we have:
v2=A2ω2cos2(ωt+ϕ)
a2=A2ω4sin2(ωt+ϕ)
Step 5: Express sin2 and cos2 in terms of v2 and a2
From the identities sin2(θ)+cos2(θ)=1, we can express:
sin2(ωt+ϕ)=a2A2ω4
cos2(ωt+ϕ)=v2A2ω2
Step 6: Formulate the relationship
Substituting these into the identity gives:
a2A2ω4+v2A2ω2=1
Multiplying through by A2ω4 yields:
a2+v2ω2=A2ω4
Step 7: Identify the graph
This equation represents an ellipse in the v2 vs a2 plane, where:
- The term a2 corresponds to one axis,
- The term v2ω2 corresponds to the other axis.
Conclusion
Thus, the graph of the square of the velocity against the square of the acceleration in simple harmonic motion is an ellipse.
In simple harmonic motion, the displacement x can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
The velocity v is the derivative of displacement with respect to time:
v=dxdt=Aωcos(ωt+ϕ)
Thus, the square of the velocity is:
v2=(Aωcos(ωt+ϕ))2=A2ω2cos2(ωt+ϕ)
The acceleration a is the derivative of velocity with respect to time:
a=dvdt=−Aω2sin(ωt+ϕ)
Thus, the square of the acceleration is:
a2=(−Aω2sin(ωt+ϕ))2=A2ω4sin2(ωt+ϕ)
Now we have:
v2=A2ω2cos2(ωt+ϕ)
a2=A2ω4sin2(ωt+ϕ)
From the identities sin2(θ)+cos2(θ)=1, we can express:
sin2(ωt+ϕ)=a2A2ω4
cos2(ωt+ϕ)=v2A2ω2
Substituting these into the identity gives:
a2A2ω4+v2A2ω2=1
Multiplying through by A2ω4 yields:
a2+v2ω2=A2ω4
This equation represents an ellipse in the v2 vs a2 plane, where:
- The term a2 corresponds to one axis,
- The term v2ω2 corresponds to the other axis.
Thus, the graph of the square of the velocity against the square of the acceleration in simple harmonic motion is an ellipse.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
The equation of motion of a simple harmonic motion is
Ad2xdt2=−ω2xBd2xdt2=−ω2tCd2xdt2=−ωxDd2xdt2=−ωtIf x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
AaTvBaT+2πvCaTxDa2T+4π2v2The time period of simple harmonic motion depends upon
AamplitudeBenergyCphase constantDmass
Define simple harmonic motion ?
View SolutionThe equation of motion of a simple harmonic motion is not
View SolutionThe average acceleration in one time period in a simple harmonic motion is
View SolutionThe oscillatory motion is simple harmonic motion since
View SolutionIf x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
View Solution
