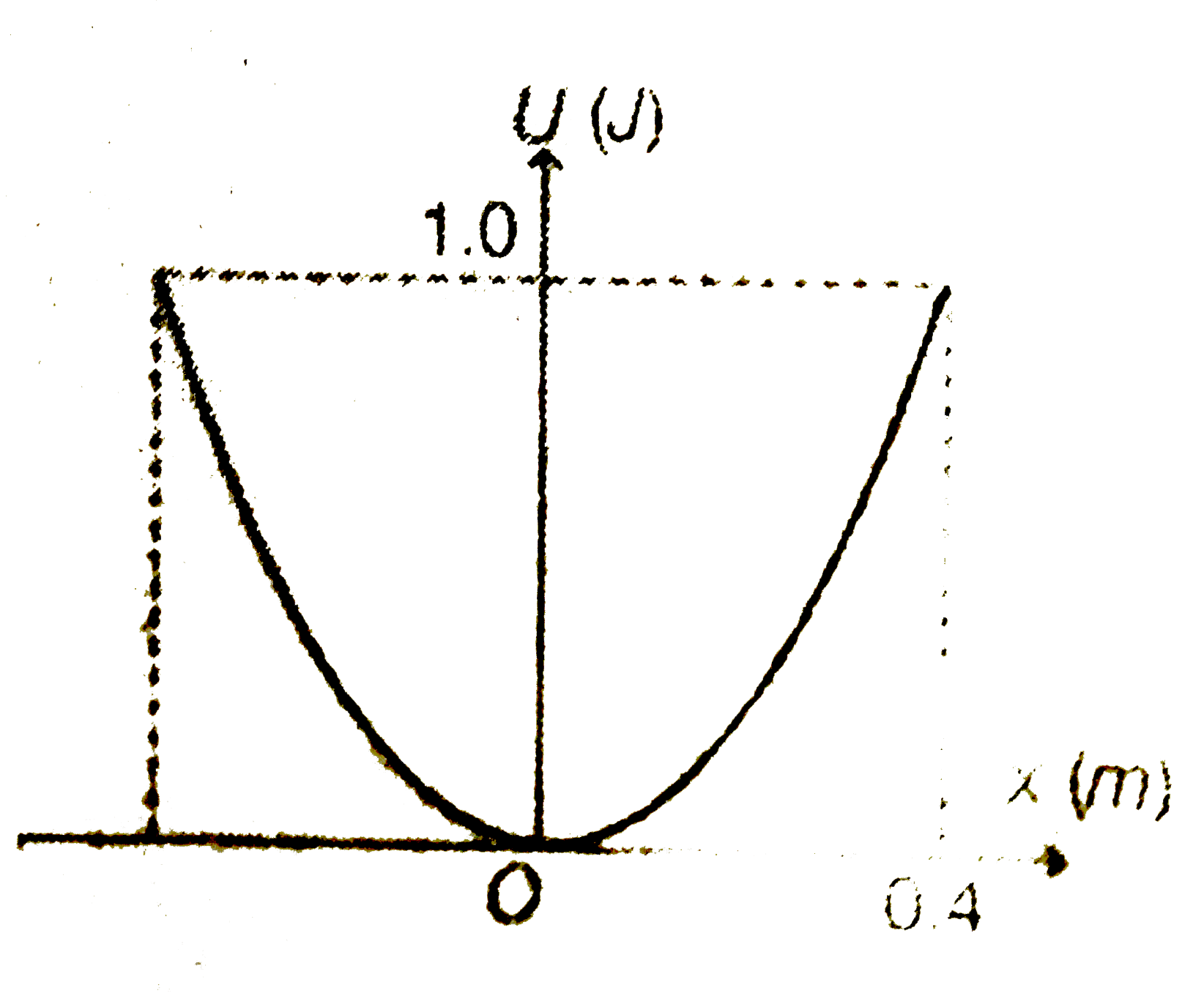
A particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
2π√mk+4√2Emg2
2π√mk
π√mk+2√2Emg2
2√2Emg2
The correct Answer is:C
For x<0
F=−dUdx=−kx
ma=−kx
or a=−kmx
−ω21x=−kmx
ω1=√km
T1=2π√mk
For x>0 U=mgx
F=−dvdx=−mg
But E=12mv20
v0=√2Em
It is speed at lowest point
T2=2v0g=2g√2Em
T=T12+T2=π√mk+2g√2Em
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A particle of mass m has momentum p. Its kinetic energy will be
View SolutionA particle of mass m is moved from A to B as show in figure. Then potential energy of the the particle
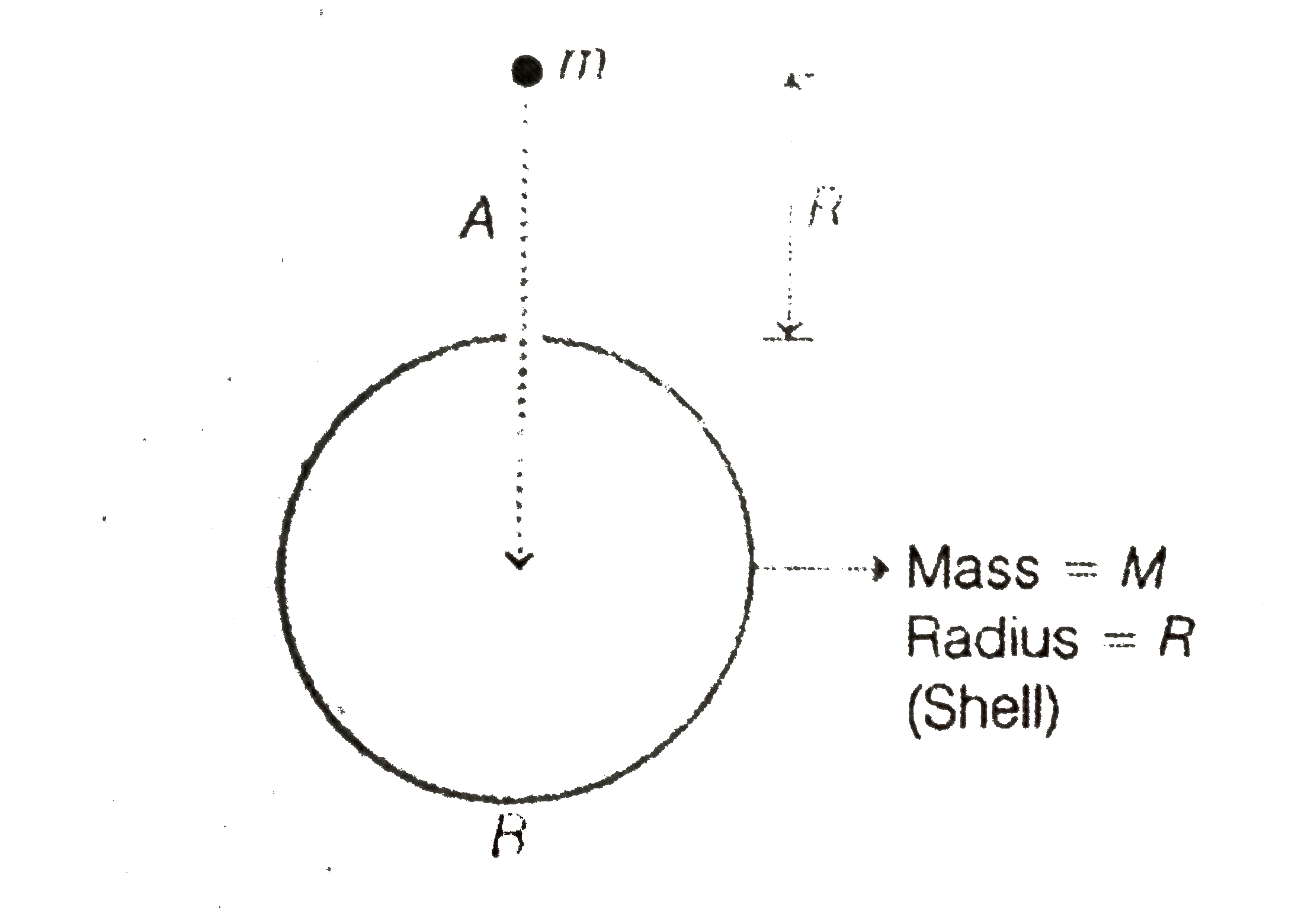 View Solution
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
 View Solution
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
 View Solution
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
 View Solution
View SolutionA small particle of mass m, moves in such a way that the potential energy U=ar3, where a is position constant and r is the distance of the particle from the origin. Assuming Rutherford's model of circular orbits, then relation between K.E and P.E of the particle is :
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View SolutionA particle of mass m is executing osciallations about the origin on the x-axis with amplitude A. its potential energy is given as U(x)=αx4, where α is a positive constant. The x-coordinate of mass where potential energy is one-third the kinetic energy of particle is
View SolutionA particle of mass m has half the kinetic energy of another particle of mass m2. If the speed of the heavier particle is increased by 2ms−1 its new kinetic energy becomes equal to t he original kinetic energy of the lighter particle. The ratio of the orighinal speeds of the lighter and heavier particle is
View SolutionA particle executing SHM has potential energy U0sin2ωt. The maximum kinetic energy and total energy respectively are
View Solution

