A gun is mounted on a gun carriage movable on a smooth plane the gun is elevated at an angle α to the horizontal . A shot, fired leaves the gun in a direction inclined at an angle θ to the horizontal . If the mass of the gum and its carriage be n times that of short , find tanθ:tanα .
To solve the problem, we need to analyze the motion of the gun and the projectile fired from it. We will use the principles of momentum conservation and the relationships between the angles and velocities involved.
1. Identify the Masses:
- Let the mass of the shot be m.
- The mass of the gun and its carriage is n×m.
2. Define the Angles:
- The gun is elevated at an angle α to the horizontal.
- The shot leaves the gun at an angle θ to the horizontal.
3. Components of Velocity:
- When the shot is fired, it has a velocity v which can be resolved into two components:
- Horizontal component: vcosα
- Vertical component: vsinα
4. Velocity of the Gun:
- Since the gun is mounted on a carriage that can move, when the shot is fired, the gun will also have a horizontal velocity v0 due to the recoil.
- The horizontal motion of the gun and the shot must satisfy the conservation of momentum.
5. Conservation of Momentum:
- Before firing, the total momentum is zero (the system is at rest).
- After firing, the momentum of the shot plus the momentum of the gun must still equal zero:
m(vcosθ)−nmv0=0
- Rearranging gives:
vcosθ=nv0
6. Relate v0 to v:
- The horizontal velocity of the gun after firing can be expressed as:
v0=vcosαn+1
- Substitute this into the momentum equation:
vcosθ=n(vcosαn+1)
7. Simplifying the Equation:
- Cancel v (assuming v≠0):
cosθ=ncosαn+1
8. Finding tanθ and tanα:
- From the definition of tangent, we have:
tanθ=sinθcosθandtanα=sinαcosα
- Using the relationship we derived, we can express tanθ:
tanθ=sinθncosαn+1=(n+1)sinθncosα
9. Final Ratio:
- The ratio tanθtanα can now be expressed as:
tanθtanα=(n+1)sinθcosαnsinαcosθ
- Since we know sinθ and cosθ can be related through the angles, we can derive the final relation.
10. Conclusion:
- After simplification, we find:
tanθtanα=1
- Thus, tanθ:tanα=1:1.
- Let the mass of the shot be m.
- The mass of the gun and its carriage is n×m.
- The gun is elevated at an angle α to the horizontal.
- The shot leaves the gun at an angle θ to the horizontal.
- When the shot is fired, it has a velocity v which can be resolved into two components:
- Horizontal component: vcosα
- Vertical component: vsinα
- Since the gun is mounted on a carriage that can move, when the shot is fired, the gun will also have a horizontal velocity v0 due to the recoil.
- The horizontal motion of the gun and the shot must satisfy the conservation of momentum.
- Before firing, the total momentum is zero (the system is at rest).
- After firing, the momentum of the shot plus the momentum of the gun must still equal zero:
m(vcosθ)−nmv0=0
- Rearranging gives:
vcosθ=nv0
- The horizontal velocity of the gun after firing can be expressed as:
v0=vcosαn+1
- Substitute this into the momentum equation:
vcosθ=n(vcosαn+1)
- Cancel v (assuming v≠0):
cosθ=ncosαn+1
- From the definition of tangent, we have:
tanθ=sinθcosθandtanα=sinαcosα
- Using the relationship we derived, we can express tanθ:
tanθ=sinθncosαn+1=(n+1)sinθncosα
- The ratio tanθtanα can now be expressed as:
tanθtanα=(n+1)sinθcosαnsinαcosθ
- Since we know sinθ and cosθ can be related through the angles, we can derive the final relation.
- After simplification, we find:
tanθtanα=1
- Thus, tanθ:tanα=1:1.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - NUMERICAL EXERCISE (LEVEL -2)
19 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direction of motion makes an angle α with the horizontal.
View SolutionA projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direcrtion of motion makes an angle α with the horizontal.
View SolutionA gun fires a bullet. The barrel of the gun is inclined at an angle of 45∘ with horizontal. When the bullet leaves the barrel it will be travelling at an angle greater than 45∘ with the horizontal. Is this statement true or false?
View SolutionA gun fires a bullet. The barrel of the gun is inclined at an angle of 45∘ with horizontal. When the bullet leaves the barrel it will be travelling at an angle greater than 45∘ with the horizontal. Is this statement true or false?
View SolutionA shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
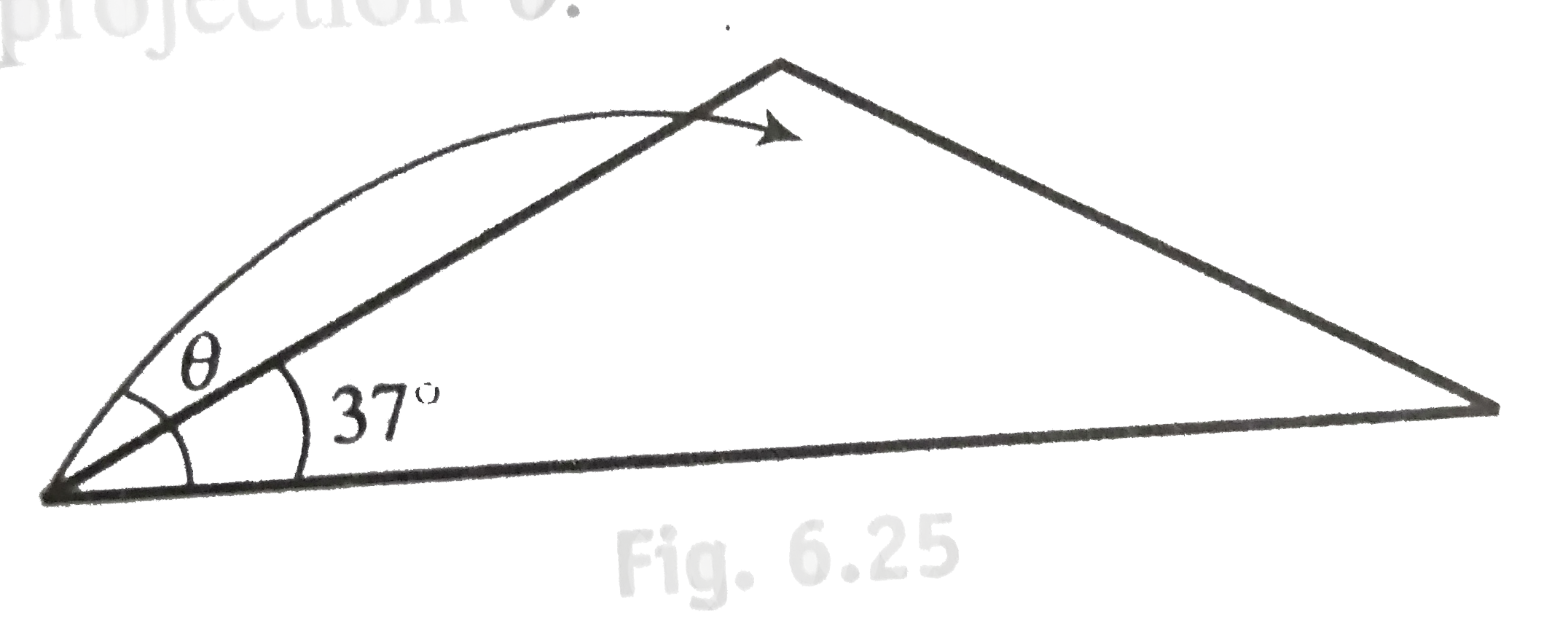
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
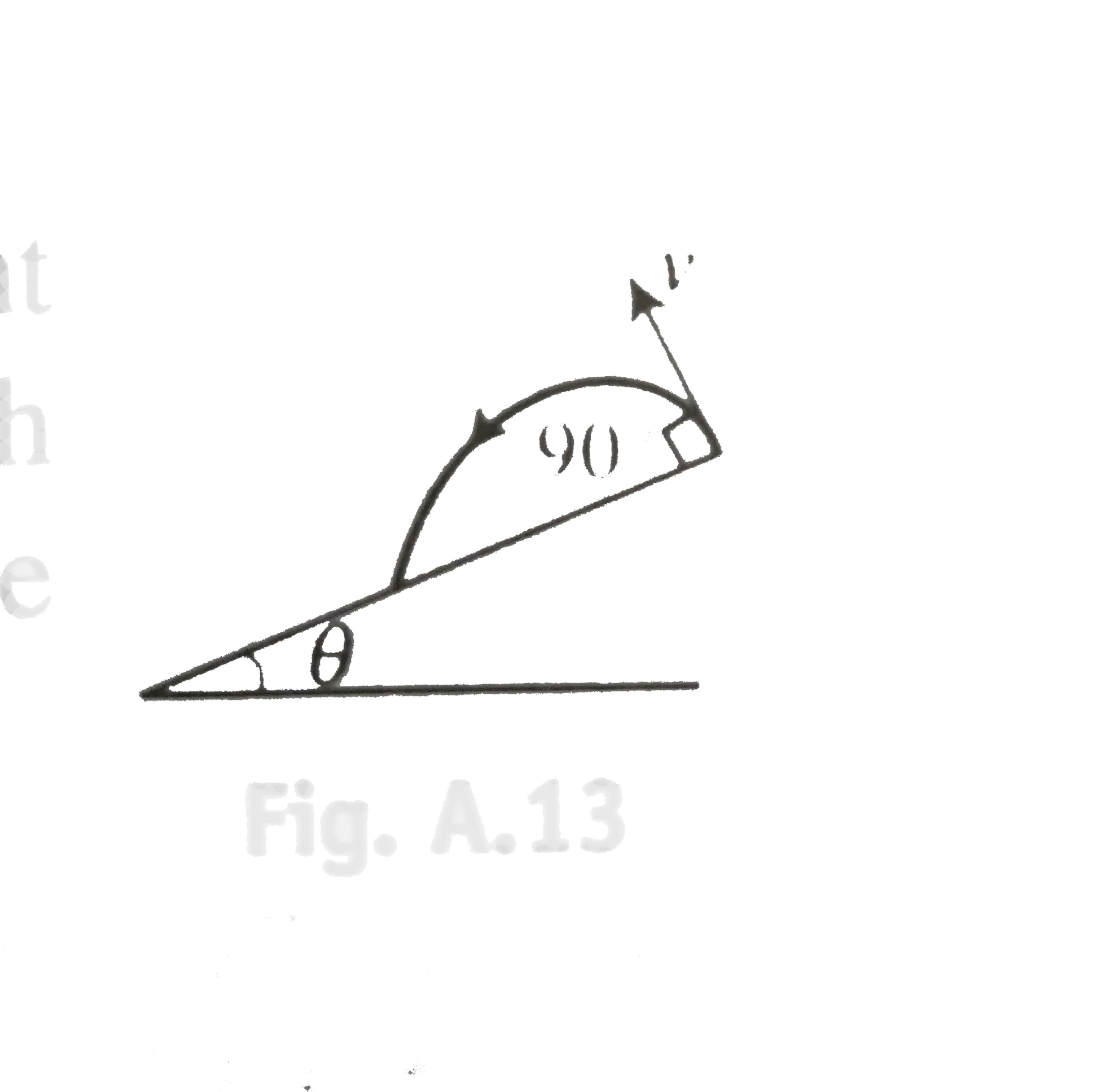
View SolutionWhen a shot is fired from a gun, the gun gets recoiled. Explain.
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View Solution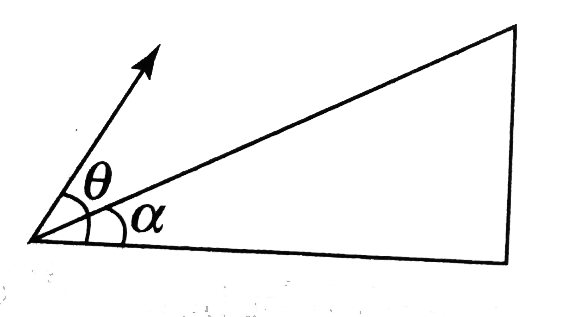
A projectile is fired at an angle θ with the horizontal. Find the condition under which it lands perpendicular on an inclined plane inclination α as shown figure.
View Solution
