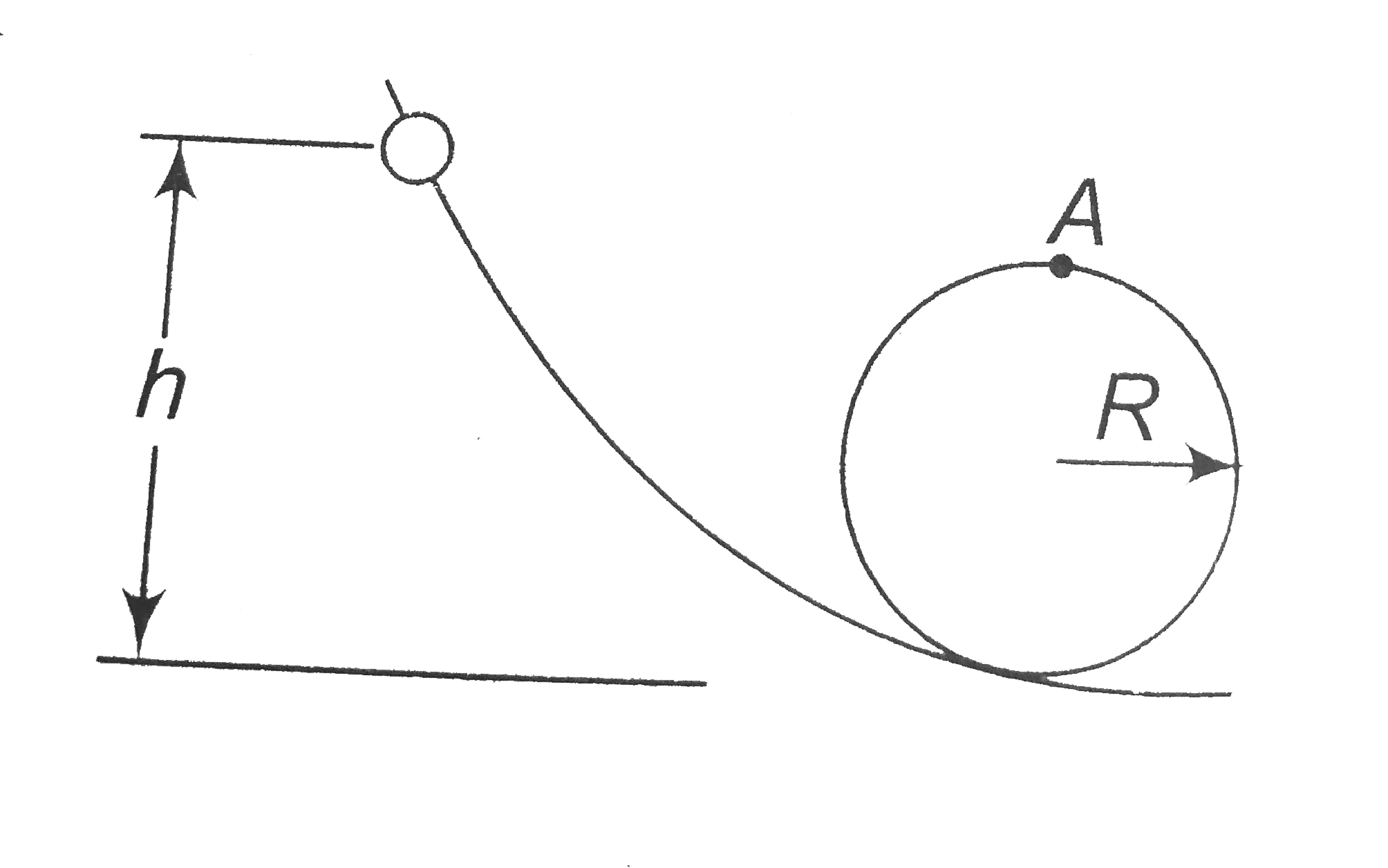
A head slide without friction around a loop the (figure). The bead slide is released is from rest at a height h=3.50R. How large is the normal force on the bead at point (A) if its mass is 50g ?
0.10N downward
0.10N upward
1.0N downward
1.0N upward
The correct Answer is:C
The speed at the top can be found from the conservatiobn of energy for the bead-track -Earth system .
We define the bottom of the loop as the zero level for the gravational potential energy.
Since v1=0,Ei=Ki=Ui=0+mgh=mg(3.50R)
The total energy of the bead at point , (A) can be
written as EA−KA+UA=12mv2A+mg(2R)
Since mechainical energy is conserved Ei+EA, we get
mg(3.50R)=12mv2A+mg(2R)
simplifying v2A=3.0gR⇒vA=√3.0gR
To find the force at the top , we constant a force diagram as shown.
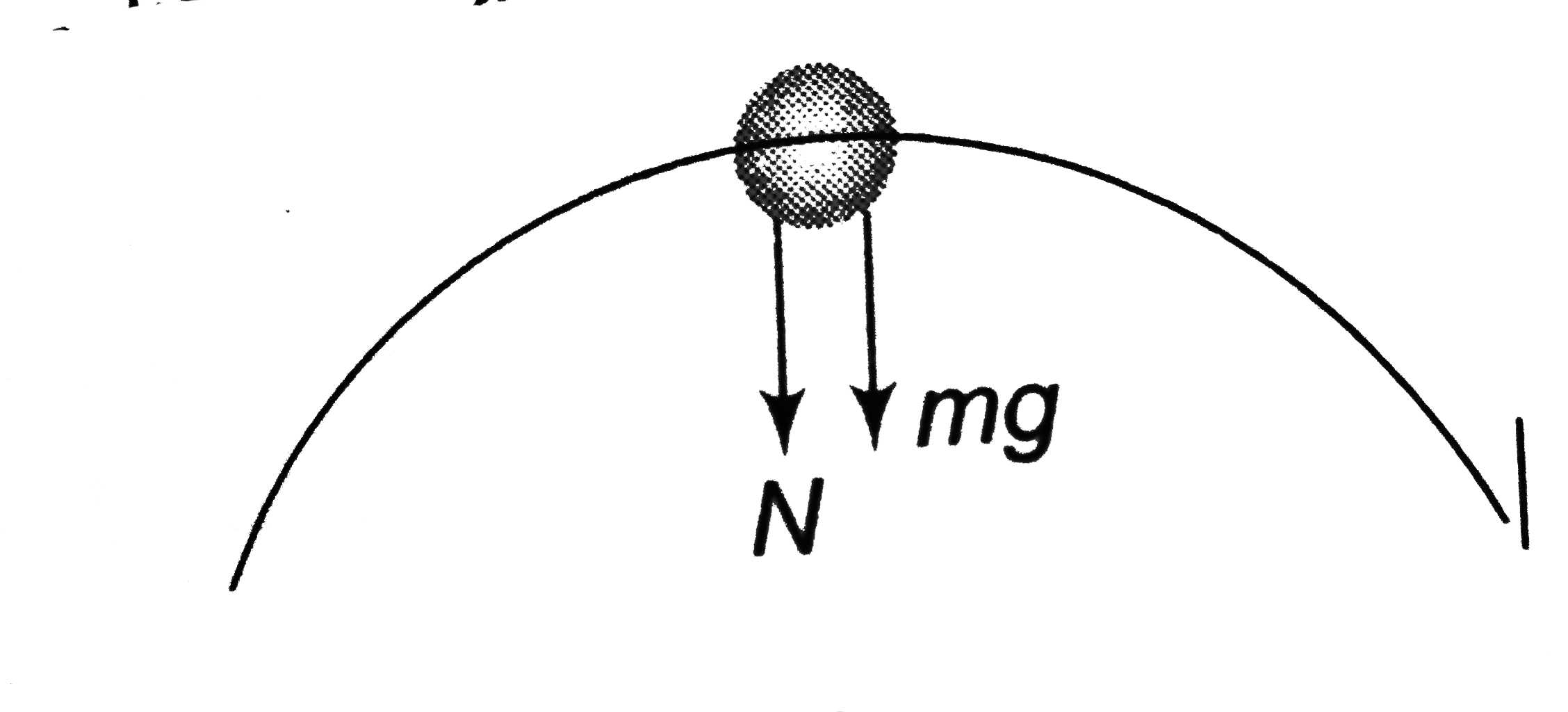
Here we assume that N is downward, like mg
ΣFy=may:N+mg=mv2r
N=m[v2R−g]=m[3.0gRR−g]=2.0mg
N=2.0(50×10−3kg)(10.0m/s2)
=1.0N downward.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts
32 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
A block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest t A what is its speed at B?

View SolutionA child slides without friction from a height h along a curved water slide (figure). She is launched from a height h/5 into the pool. Determine her maximum airbone height y in terms of h and θ.

View Solution
Knowledge Check
A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
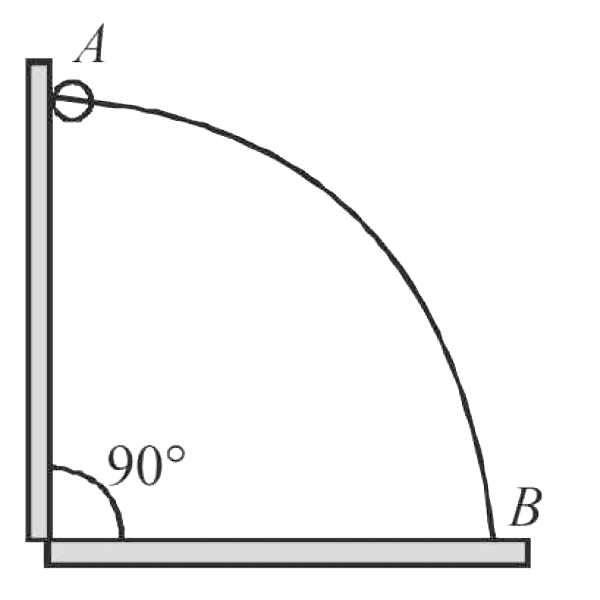 Aalways radially outwardsBalways radially inwardsCraidally outwards initially and inwards laterDradially inwards initially and radially outwards later
Aalways radially outwardsBalways radially inwardsCraidally outwards initially and inwards laterDradially inwards initially and radially outwards laterA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
 Ag2B(√3g)(2)Cg√2Dg
Ag2B(√3g)(2)Cg√2DgA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
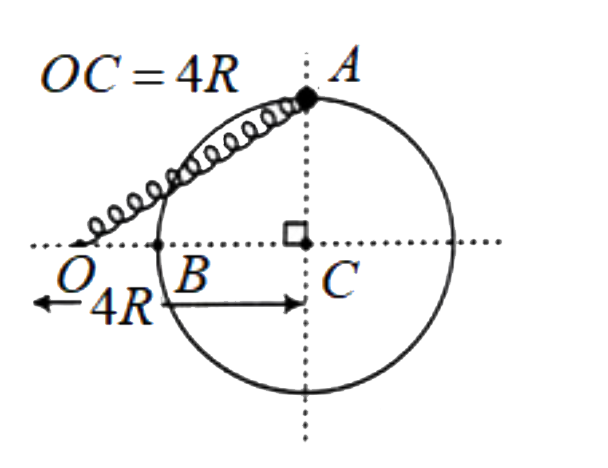 A252kR2B92kR2C8kR2D12KR2
A252kR2B92kR2C8kR2D12KR2
A small toy car of mass m slides with negligible friction on a ''loop'' the loop track as shown in Fig.3E.32. The toy car starts from rest at a point H above the level of the lowest point of the track
(a) If H=2R, what normal force is exerted by the track on the toy car at point q?. What are the speed and normal force at point r ?
(b) At what height will the ball leave the track and to what maxiumum height will it rise afterwards ?
(c) If H=4R, what is the speed and normal reaction reaction at point s ?

View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionA massless ring hangs from a thread and two beads of mass m slide it without friction. The beads are released simultaneously from the top of the ring and slide down along possible sides. Find the angle from vertical at which the ring will start to rise.

View SolutionAs shown in the figure, a cube of mass m starts from rest from point 1 at a height 4R, where R is the radius of the circular track. The cube slides down the frictionless track and goes around the loop as shown. The force which the track exerts on the cube at point. 2 is βmg. Find β.
'(##CEN_KSR_PHY_JEE_C07_005_Q03##)'
View SolutionA ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if m>3M2 . ltbr>
View Solution
