A heavy iron bar of weight is having its one end on the ground and the other on the shoulder of a man The rod makes an angle with the horizontal What is the weight experienced by the man ?
The correct Answer is:d
To solve the problem, we need to analyze the forces acting on the heavy iron bar and apply the principles of equilibrium and torque. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a heavy iron bar of weight W resting on the ground at one end and on the shoulder of a man at the other end. The bar makes an angle θ with the horizontal.
Step 2: Identify Forces Acting on the Bar
1. The weight of the bar W acts downwards at its center of mass, which is located at the midpoint of the bar.
2. The force exerted by the man on the bar (let's call it F1) acts upwards at the point where the bar rests on his shoulder.
3. The ground exerts a force (let's call it F2) upwards at the point where the bar touches the ground.
Step 3: Apply the Equilibrium Condition
For the bar to be in equilibrium:
- The sum of the upward forces must equal the sum of the downward forces.
This gives us the equation:
F1+F2=W(1)
Step 4: Analyze Torque
To find the force F1, we can analyze the torques about the point where the bar touches the ground. The torque due to the weight of the bar will cause a clockwise rotation, while the torque due to the force F1 will cause a counterclockwise rotation.
1. The torque due to the weight W at the center of the bar (which is at a distance L2 from the ground) is:
Torque due to W=W⋅(L2cosθ)
2. The torque due to the force F1 (which acts at a distance L from the ground) is:
Torque due to F1=F1⋅(Lsinθ)
Setting the sum of torques to zero for equilibrium:
W⋅(L2cosθ)=F1⋅(Lsinθ)(2)
Step 5: Solve for F1
From equation (2), we can simplify:
W⋅L2cosθ=F1⋅Lsinθ
Dividing both sides by L:
W2cosθ=F1sinθ
Now, solving for F1:
F1=Wcosθ2sinθ
Step 6: Final Expression for Weight Experienced by the Man
The weight experienced by the man is equal to the force F1:
F1=Wcosθ2sinθ
Conclusion
Thus, the weight experienced by the man is given by:
F1=Wcosθ2sinθ
We have a heavy iron bar of weight W resting on the ground at one end and on the shoulder of a man at the other end. The bar makes an angle θ with the horizontal.
1. The weight of the bar W acts downwards at its center of mass, which is located at the midpoint of the bar.
2. The force exerted by the man on the bar (let's call it F1) acts upwards at the point where the bar rests on his shoulder.
3. The ground exerts a force (let's call it F2) upwards at the point where the bar touches the ground.
For the bar to be in equilibrium:
- The sum of the upward forces must equal the sum of the downward forces.
This gives us the equation:
F1+F2=W(1)
To find the force F1, we can analyze the torques about the point where the bar touches the ground. The torque due to the weight of the bar will cause a clockwise rotation, while the torque due to the force F1 will cause a counterclockwise rotation.
Torque due to W=W⋅(L2cosθ)
Torque due to F1=F1⋅(Lsinθ)
W⋅(L2cosθ)=F1⋅(Lsinθ)(2)
From equation (2), we can simplify:
W⋅L2cosθ=F1⋅Lsinθ
Dividing both sides by L:
W2cosθ=F1sinθ
Now, solving for F1:
F1=Wcosθ2sinθ
The weight experienced by the man is equal to the force F1:
F1=Wcosθ2sinθ
Thus, the weight experienced by the man is given by:
F1=Wcosθ2sinθ
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Integer Type Questions
7 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Problems for practice
112 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
A board is balanced on a rough horizontal semicircular log. Equilibrium is obtained with the help of addition of a weight to one of the ends of the board when the board makes an angle θwith the horizontal. Coefficient of friction between the log and the board is
View SolutionIn figure a thin horizontal bar AB of negligible weight and length L is pinned to a vertical wall at A and supported at B by a thin wire BC that makes an angle θ with the horizontal. A weight W can be moved anywhere along the bar; its position is defined by the distance x from the wall of its centre of mass. As a function of x, the horizontal component of the reaction at the hinge A is?
View Solution
Knowledge Check
A uniform rod of length L and weight WR is suspended as shown in the accompanying figure. A weight W is added to the end of the rod. The rod rests in horizontal position and is hinged at O. the support wire is at an angle θ to the rod. What is the tension T in the wire ?
 AT=WsinθBT=W+WRCT=W+1/2WRDT=W+1/2WRsinθ
AT=WsinθBT=W+WRCT=W+1/2WRDT=W+1/2WRsinθA rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
Av0cotθBv0cosθCv0sinθDv0tanθA man weighing 100 kg carriesa load of 10kg on his head. He jumps from a tower with the load on his head. What will be the weight of the load as experienced by the man?
AzeroB10kgCslightly more than 10 kgD110 kg
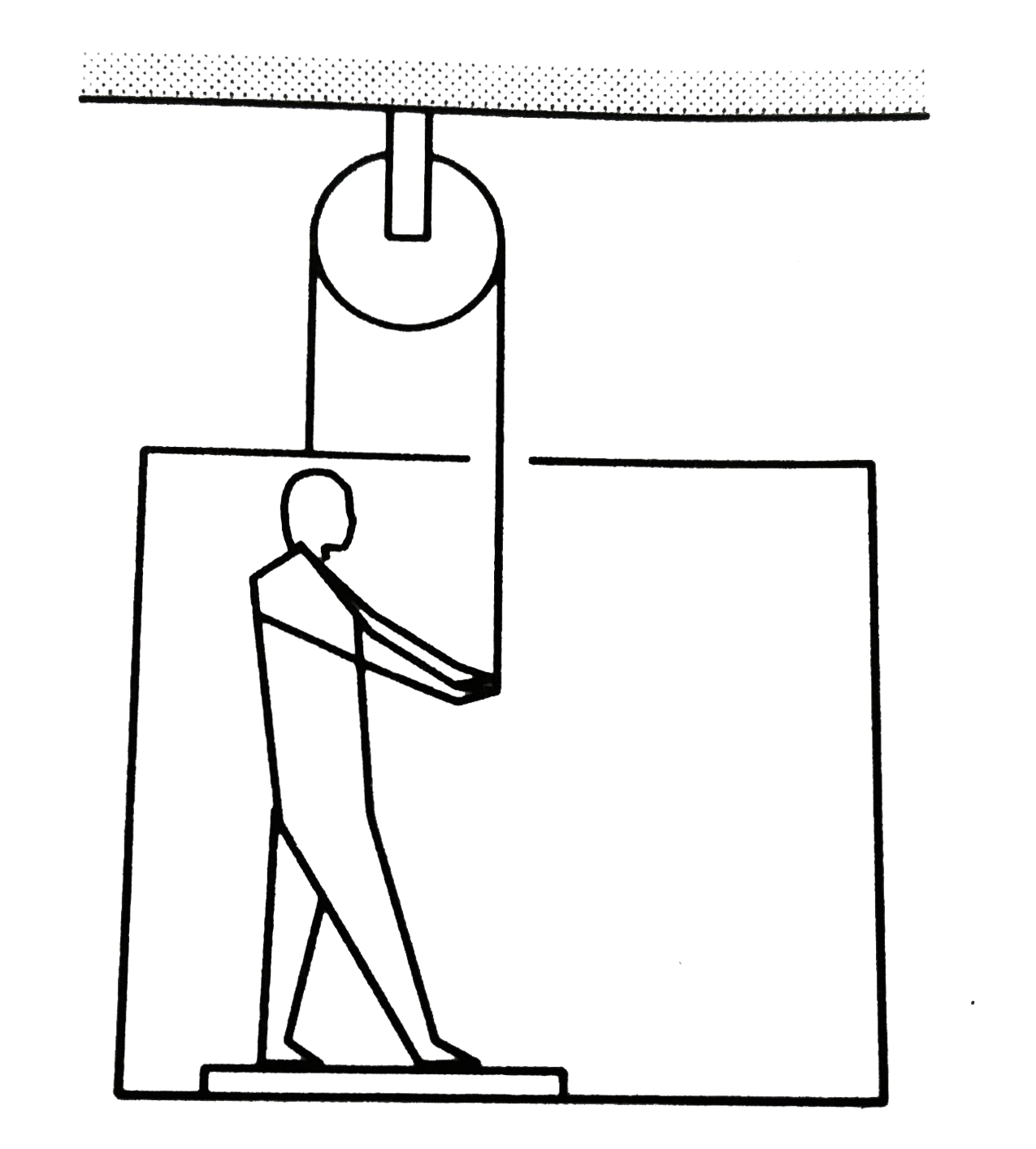
Figure shows a man of mass 60 kg standing on a light weighting machine kept in a box of mass 30 kg. The box is haning from a pulley fixed to the ceiling through a light rope, the other end of which is held by the man himswelf. If the man manages to keepthe box at rest, what is the weight shown by the man manages to keep the box at rest, what is the weight shown by the machine? What force should he exert on the rope to get his correct weight on the machine?
View SolutionA thin horizontal bar AB of negligible mass and length l is hinged to a vertical wall at A and supported at B by thin wire BC which is tied to a point C vertically above in the same wall.BC makes angle θ with the horizontal . A weight W is moved along the bar. Show how the tensile force T in the thin wire changes with the distance x of the weight from the wall.
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
View SolutionA horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to
View Solution
