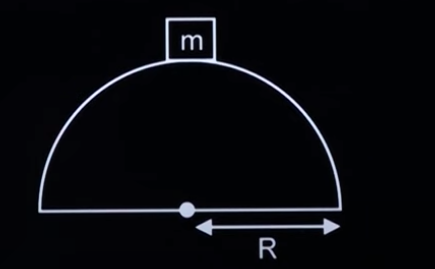
A hemisphere of radius $R$ and of mass $4 m$ is free to Slide with its base on a smooth horizontal table. A particle mass $m$ is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement $θ$ when velocity of hemisphere has become $v$ .

Text Solution

Verified by Experts

Actual velocilty of ball is $v_{1}$ is horizontal direction.
$∴ v_{1} - (- v) = v_{r e l} cos θ$
$∴ v_{1} + v = v_{r e l} cos θ$ ……….i

Applying conservation principle of momentum in horizotal direction.
$P_{i x} = P_{f x}$
$0 = m v_{1} - 4 m v$
$∴ v_{1} = 4 v$ .......ii
Applying mechanic energy conservation principle.
Loss in $P E =$ gain in $K E$
$m g (r - r cos θ) = \frac{1}{2} m {[\sqrt{v_{1}^{2} + {(v_{r e l} s i θ)}_{r e l}^{2}}]}^{2} + \frac{1}{24} m v^{2}$ .........iiii
after solving eqn i , ii , iii
$v_{r e l} = \frac{5 v}{cos θ}$
$∴ ω_{r e l} = \frac{v_{r e l}}{R} = \frac{5 v}{R cos θ}$

Updated on:21/07/2023