A hollow cylindrical shell of radius R has mass M. It is completely filled with ice having mass m. It is placed on a horizontal floor connected to a spring (force constant k) as shown. When it is disturbed it performs oscillations without slipping on the floor.
(a) Find time period of oscillation assuming that the ice is tightly pressed against the inner surface of the cylinder.
(b) If the ice melts into non viscous water, find the time period of oscillations. (Neglect any volume change due to melting of ice)
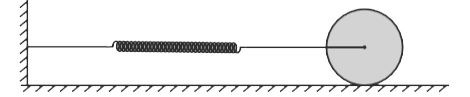
The correct Answer is:(a) 2pi sqrt((4M+3m)/(2K));<br>(b) 2pi sqrt((2M +m)/(K))
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS159videos
ROTATIONAL MOTION
- BOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension33videos
SURFACE TENSION
Similar Questions
A semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is R
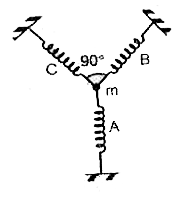
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
. View Solution
Knowledge Check
- Question 1 - Select One
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations isA2π√mkBπ√mk+π√mk2Cπ√m3k2Dπ√mk+π√m2k - Question 2 - Select One
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
. View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
. View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View Solution-
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations isView Solution