A hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T2>T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2 .Solution in Tamil
The correct Answer is:A, B
T2>T1
A=π(R22−R21)
so,dQdt=KA(T2−T1)l
=Kπ(R22−R21)(T2−T1)l
considering a concentric cylindtical cell of radius R and thickness DR.The radial heat flow through the cell.
H=(dQ)/(dt)=-KA(d theta)/(dr)<br>[-ve because as r increases Q decreases]<br>A=2 pi rl,<br>H=-2 pi rl K(d theta)/(dr)<br>or, int_(r_1)^(r_2)(dr)/r=-(2 pi rlK)/H int_(T_1)^(T_2)d theta<br>Integrat∈gandsimplify∈gwe≥t<br>H=(dQ)/(dt)=(2 pi Kl(T_2-T_1))/(In(R_2//R_1)).

Topper's Solved these Questions
Similar Questions
A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registered at 140°F. What is the fall in temperature as registered by the centigrade thermometer ?
View SolutionThe steam point and the ice point of a mercury thermometer are marked as 80∘C and 20∘C. What will be the temperature in centigrade mercury scale when this thermometer reads 32∘C?
View SolutionFind the dimensions of
a. linear momentum
b. frequency and
c. pressure
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA spherical shell of inner radius R1 and outer radius R2 is having variable Where 'r' is the distance from the centre Two surface of the shell are maintained at temperature T1 respectively (T1<T2) The heat current flowing through the shell would be .
View SolutionThe wall of a house is made of two different materials of same thickness. The temperatures of the outer wall is T2 and that of inner wall is T1<T2. The temperature variation inside the wall as shown in the figure. Then :
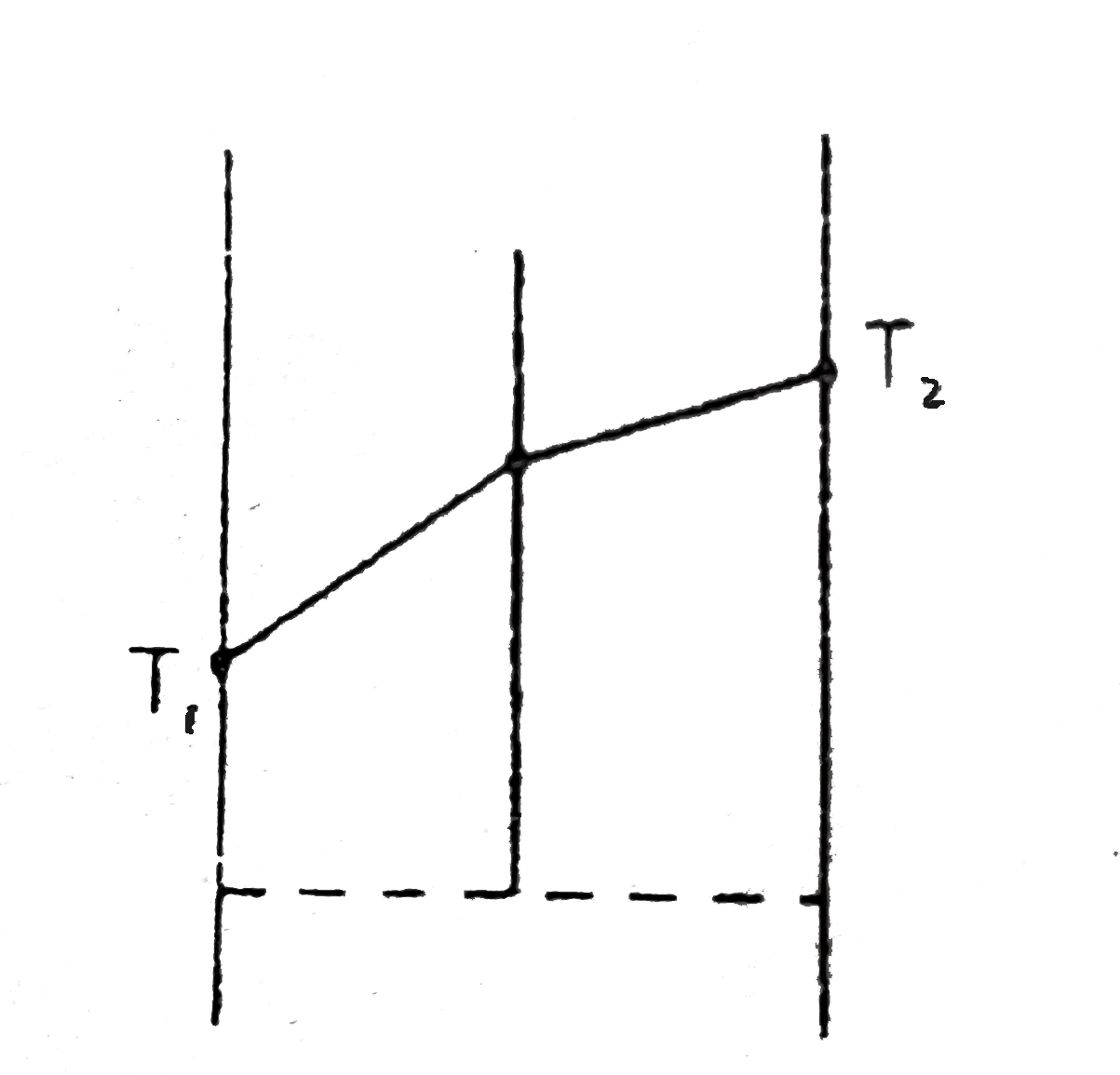
View Solution(i) A cylindrical pipe of length L has inner and outer radii as a and b respectively. The inner surface of the pipe is at a temperature T1 and the outer surface is at a lower temperature of T2. Calculate the radial heat current if conductivity of the mate- rial is K.
(ii) A cylindrical pipe of length L has two layers of material of conduc- tivity K1 and K2. (see figure). If the inner wall of the cylinder is maintained at T1 and outer surface is at T2(<T1), calcu- late the radial rate of heat flow.
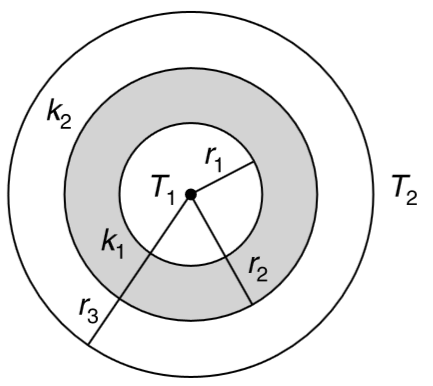
View SolutionA thick cylindrical shell made of material of thermal conductivity k has inner and outer radii r and R respectively and its length is L. When the curved surface of the cylinder are lagged (i.e., given insulation cover) and one end is maintained at temperature T_(1) and the other end is maintained at T_(2)(lt T_(1)) , the heat current along the length of the cylinder is H. In another experiment the two ends are lagged and the inner wall and outer wall are maintained at T_(1) and T_(2) respectively. Find the radial heat flow in this case.
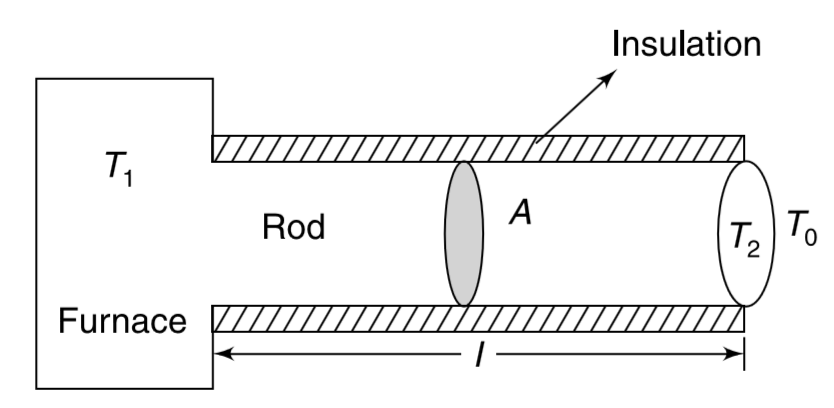
View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = alpha T, where alpha is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T_(1) and T_(2) (T_(1)gtT_(2)) . Heat current flowing through the rod will be
View SolutionThe space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
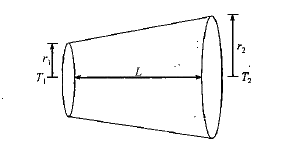
View SolutionFind the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
View SolutionCurved surface of a uniform rod is isolated from surrounding. Ends of the rod are maintained at temperatures T1 and T2(T1>T2) for a long time. At an instant, temperature T1 starts to decrease at a constant and slow rate. If thermal capacity of material of the rod is considered, then which of thefollowing statements is/are correct ?
View SolutionTwo closed vessel A and B of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a naroow open tube. If th temperature of one is now maintained at T1 and other at T2 (wehre T1>T2 ) then that what will be the final pressure ?
View SolutionConstant temperature of ends are T1 and T2 (where T1>T2) for a conducting rod of 'L' length and cross-sectional area A. What would be the rate of heat transfer in thermal steady state ?
View SolutionActivity of a radioactive substance is Rt at time t1 and R2 at time t2(t2>t1). Then the ratio R2R1 is
View Solution