A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is and the furnace is maintained at . The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained . The exposed surface of the rod has emissivity e. Prove that is proportional to and find the proportionality constant.
![A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T(0) and the furnace is maintained at T(1) = T(0) + DeltaT(1). The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T(2) = T(0) + DeltaT(2) [DeltaT(2) ltlt T(0)]. The exposed surface of the rod has emissivity e. Prove that DeltaT(1) is proportional to DeltaT(2) and find the proportionality constant.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V02_C05_E05_045_Q01.png)
The correct Answer is:
Step by step video, text & image solution for A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T_(0) and the furnace is maintained at T_(1) = T_(0) + DeltaT_(1). The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T_(2) = T_(0) + DeltaT_(2) [DeltaT_(2) ltlt T_(0)]. The exposed surface of the rod has emissivity e. Prove that DeltaT_(1) is proportional to DeltaT_(2) and find the proportionality constant. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Two lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?
04:51View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
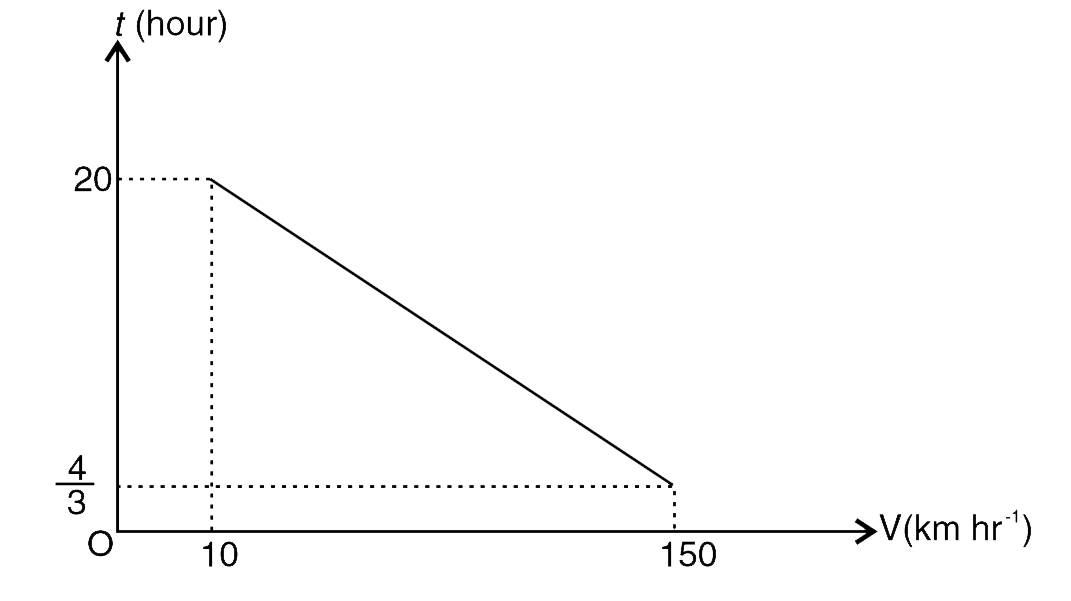
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?08:03View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmospere, find the temperature at B.
 04:25View Solution
04:25View SolutionA cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T_1 and the other end in surrounding at temperature T_2 . Surface of the rod exposed to the surrounding has emissivity e. Also T_2=T_s+DeltaT and T_sgt gt DeltaT . If T_1-T_s prop DeltaT ,find the proportionality constant.
03:02View SolutionA uniform rod of thermal conductivity of 65J//m-s-^(@)C is surrounded by an insulator on its sides. One of its ends is put in a furnace, while the other end is kept exposed. If the temperature gradient of the rod is -75^@C//m , find the emissive power of the exposed end.
08:55View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
02:13View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T_(1) . The other end of the rod is kept at at temperature T_(2) . The thermal conductivity of the material of the rod is K and emissivity of the rod is e . It is given that T_(2)=T_(S)+DeltaT where DeltaT lt lt T_(S) , T_(S) being the temperature of the surroundings. If DeltaT prop (T_(1)-T_(S)) , find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T_(2) .
06:10View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = alpha T, where alpha is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T_(1) and T_(2) (T_(1)gtT_(2)) . Heat current flowing through the rod will be
02:46View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T_(1),T_(2) and T_(3) respectively. Neglecting heat loss to the surroundings, find the temperature at B.
03:02View SolutionCurved surface of a uniform rod is isolated from surrounding. Ends of the rod are maintained at temperatures T1 and T2(T1>T2) for a long time. At an instant, temperature T1 starts to decrease at a constant and slow rate. If thermal capacity of material of the rod is considered, then which of thefollowing statements is/are correct ?
03:31View SolutionThree rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T_(1) and T_(2) as shown in the figure. As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
04:49View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
 02:12View Solution
02:12View SolutionFour identical rods AB,CD,CFandDE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l,AandK respectively. The ends A,EandF are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
 06:39View Solution
06:39View SolutionA uniform rod of thermal conductivity of 65J/m−s−∘C is surrounded by an insulator on its sides. One of its ends is put in a furnace, while the other end is kept exposed. If the temperature gradient of the rod is −75∘C/m, find the emissive power of the exposed end.
02:29View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.
 03:23View Solution
03:23View Solution

