A homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then:
η>3
η<3
η>2
η<6
The correct Answer is:D
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the System
We have a homogeneous rod of length l=ηx and mass M lying on a smooth horizontal floor. A bullet of mass m strikes the rod at a distance x from the middle of the rod with a velocity v0 perpendicular to the rod.
Step 2: Determine the Impact
When the bullet hits the rod, it comes to rest after the collision. The rod will start rotating about its center of mass due to the impact. The distance from the center of the rod to the point of impact is x.
Step 3: Analyze the Motion of the Rod
After the impact, the rod will have both translational and rotational motion. The center of mass of the rod will move, and the rod will also rotate about its center of mass.
Step 4: Calculate the Linear Momentum Change
The impulse imparted by the bullet is equal to the change in linear momentum of the rod. Since the bullet comes to rest, the change in momentum for the bullet is:
Δp=mv0
This impulse will cause the rod to gain some linear momentum.
Step 5: Calculate the Angular Impulse
The angular impulse about the center of mass due to the bullet striking at a distance x from the center is given by:
Angular Impulse=Impulse×Distance=mv0⋅x
Step 6: Relate Linear and Angular Quantities
Let ω0 be the angular velocity of the rod after the impact. The moment of inertia I of the rod about its center is:
I=112ML2=112M(ηx)2
The relationship between linear velocity V of the center of mass and angular velocity ω0 is:
V=ω0⋅L2=ω0⋅ηx2
Step 7: Set Up the Equations
From the conservation of linear momentum:
mv0=MV
Substituting for V:
mv0=M(ω0⋅ηx2)
From the angular impulse:
mv0⋅x=I⋅ω0
Substituting for I:
mv0⋅x=(112M(ηx)2)⋅ω0
Step 8: Solve for ω0
From the angular impulse equation:
ω0=12mv0⋅xM(ηx)2
Step 9: Substitute and Simplify
Now substituting ω0 back into the linear momentum equation:
mv0=M(12mv0⋅xM(ηx)2⋅ηx2)
This simplifies to:
mv0=12mv0⋅ηx2(ηx)2
Cancelling mv0 (assuming v0≠0):
1=6ηη2
Rearranging gives:
η2−6η<0
Factoring gives:
η(η−6)<0
Thus, η<6.
Conclusion
The condition for η is:
η<6
We have a homogeneous rod of length l=ηx and mass M lying on a smooth horizontal floor. A bullet of mass m strikes the rod at a distance x from the middle of the rod with a velocity v0 perpendicular to the rod.
When the bullet hits the rod, it comes to rest after the collision. The rod will start rotating about its center of mass due to the impact. The distance from the center of the rod to the point of impact is x.
After the impact, the rod will have both translational and rotational motion. The center of mass of the rod will move, and the rod will also rotate about its center of mass.
The impulse imparted by the bullet is equal to the change in linear momentum of the rod. Since the bullet comes to rest, the change in momentum for the bullet is:
Δp=mv0
This impulse will cause the rod to gain some linear momentum.
The angular impulse about the center of mass due to the bullet striking at a distance x from the center is given by:
Angular Impulse=Impulse×Distance=mv0⋅x
Let ω0 be the angular velocity of the rod after the impact. The moment of inertia I of the rod about its center is:
I=112ML2=112M(ηx)2
The relationship between linear velocity V of the center of mass and angular velocity ω0 is:
V=ω0⋅L2=ω0⋅ηx2
From the conservation of linear momentum:
mv0=MV
Substituting for V:
mv0=M(ω0⋅ηx2)
mv0⋅x=I⋅ω0
Substituting for I:
mv0⋅x=(112M(ηx)2)⋅ω0
From the angular impulse equation:
ω0=12mv0⋅xM(ηx)2
Now substituting ω0 back into the linear momentum equation:
mv0=M(12mv0⋅xM(ηx)2⋅ηx2)
This simplifies to:
mv0=12mv0⋅ηx2(ηx)2
Cancelling mv0 (assuming v0≠0):
1=6ηη2
Rearranging gives:
η2−6η<0
Factoring gives:
η(η−6)<0
Thus, η<6.
The condition for η is:
η<6
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
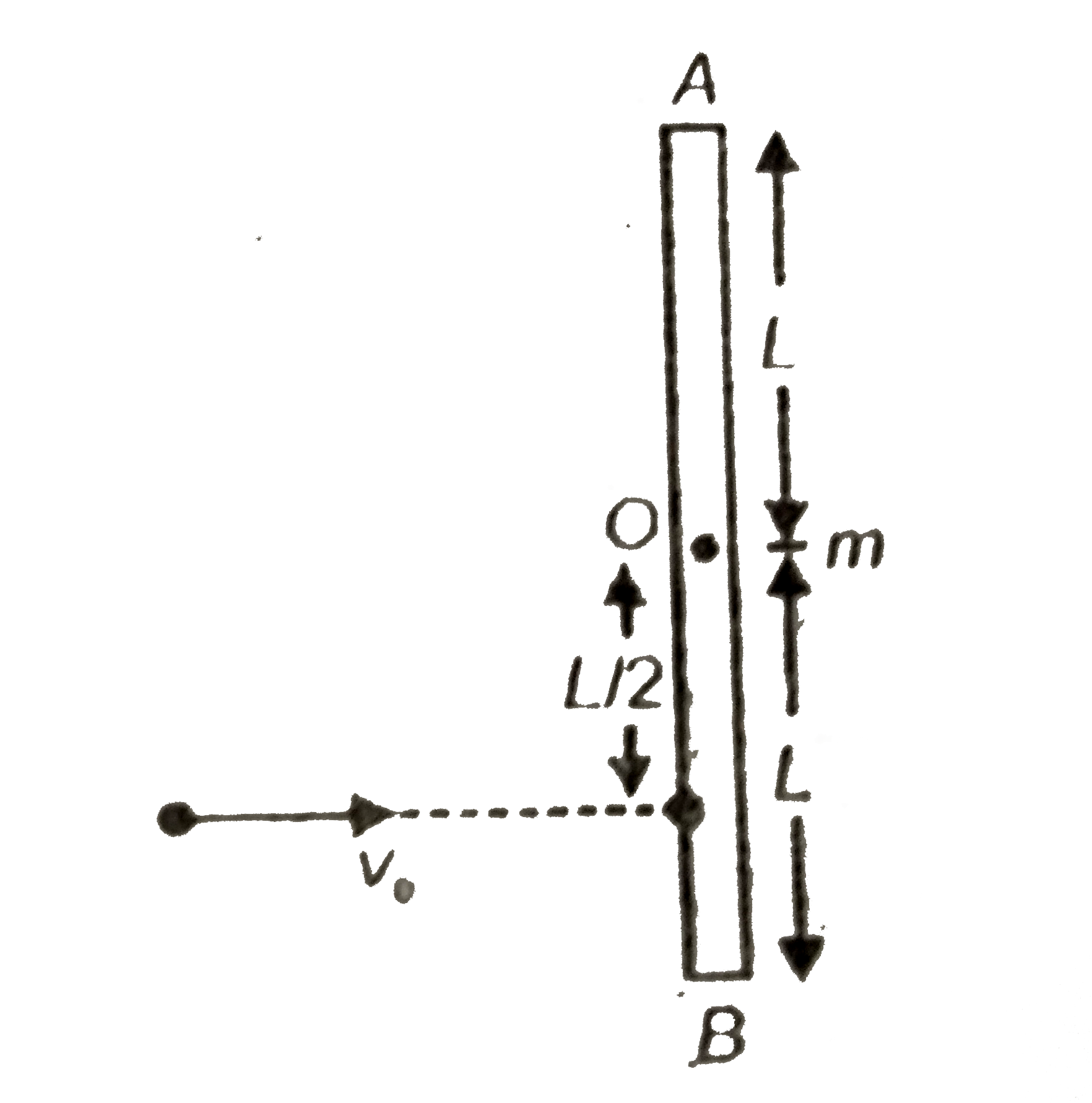
Angular velocity of rod just after collision isView SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.

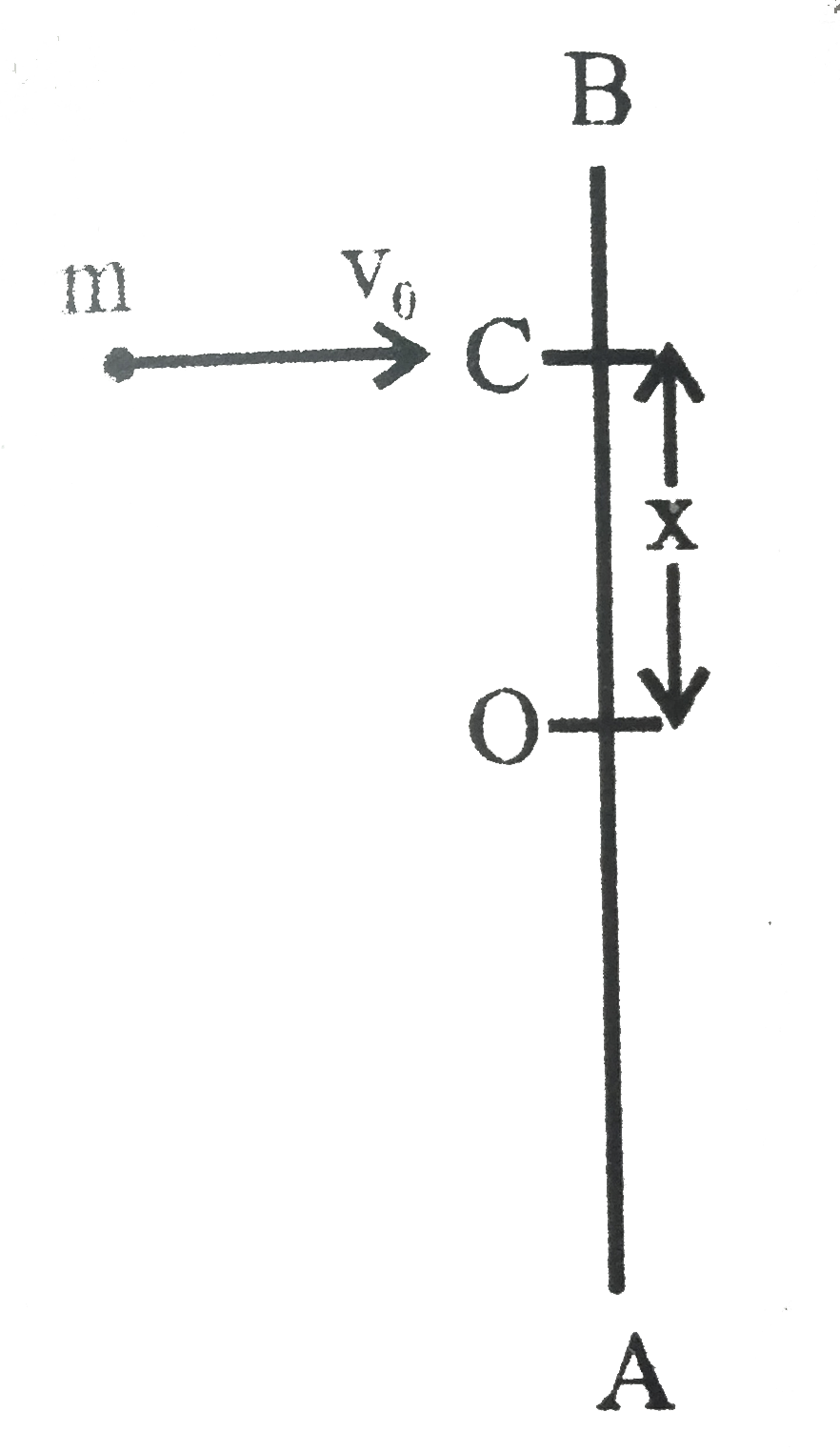
Angular velocity of rod just after collision isView SolutionA uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
 .View Solution
.View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 View Solution
View SolutionA uniform rod of lengh l moving with a downward velocity v0 strikes a peg P. If the coefficient of restitutioin of impact is e, find the velocity of CM of the rod just after impact.
 View Solution
View Solution
