A horizontal spring block system of mass M executes simple harmonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
T0=2π√Mk (i)
Let v0 be the velocity of mass M as it passes the equilibrium position. If a0 is the initial amplitude, then
12Mv2=12ka20
⇒v=(√kM)a0
If V is the combined velocity of (M+m) system in equalibrium possition, then by low of conservation of linear momentum, we have
Mv=(M+m)V
⇒V=(MM+m)v
Let a be the new amplitude, then
12ka=212(M+m)V2
=12(M+m)(MM+m)2v2
=12(M+m)M2(M+m)2(kM)a20
⇒a=a0√MM+m
New time period is
T=2π√M+mk
=√M+mMT0
{.T0=2π√Mk}
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A horizontal spring block system of mass M executes simple har monic motion.w hen the block is passingle through its equilibrium position, an object of mass m is put on it and the two move tother. Find the new amplitude and frequency of vibration.
View SolutionA block of mass M is lying on a frictionless horizontal surface and it connected to a spring of spring constant k, whose other end is fixed to a wall, system executes simple harmonic motion of amplitude A0, when the block is passing through its equilibrium positions, an object of mass m is put on it and the two move together with a new time period T and amplitude A. Find the value of T and A in terms of given constants.
View Solution
Knowledge Check
A horizontal spring-block system of mass 1kg executes SHM of amplitude 10 cm. When the block is passing through its equilibrium position another mass of 1kg is put on it and the two move together.
Aamplitude will remain unchangedBamplitude will become 5√2 cmCthe frequency of oscillations will remain sameDthe frequency of oscillations will decrease.A horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium positiojn an object of mass 1kg is put on it the two move togather The new amplitude of vibration is (A being its initial amplitude)
A√23AB√32AC√2AD√A√2A horizontal spring is connedted to a mass M. It exectues simple harmonic motion. When the mass M passes through its mean position, an object of mass m is put on it ans the two move together. The ratio of frequencies before and after will be-
A(1+mM)1/2B(1+mM)C(MM+m)1/2D(MM+m)
A block of mass M executes SHM with amplitude a and time period T. When it passes through the mean position, a lump of putty of mass m is dropped on it. Find the new amplitude and time period.
View SolutionA block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
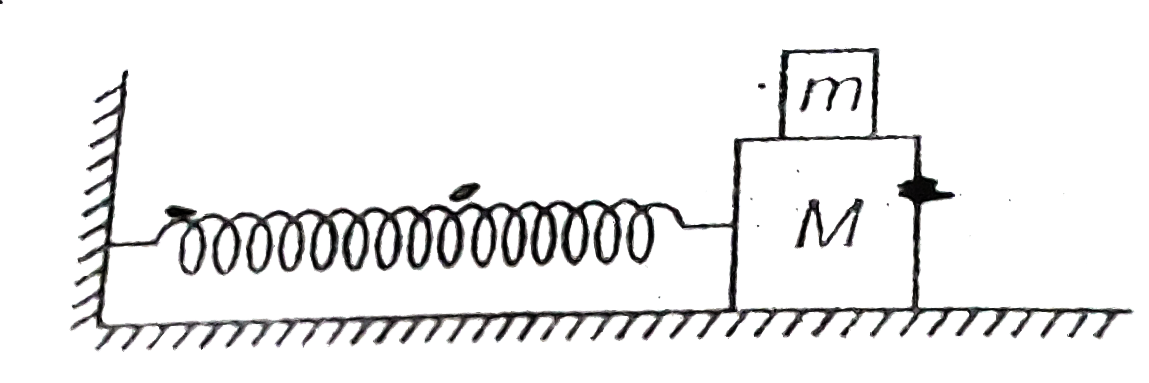
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
View SolutionConsider a horizontal spring-block system executing SHM. The block has a mass of 2 kg . When the block is at its equilibrium position, another object of mass 1 kg is put on it. Considering no slipping between the blocks, find the ratio of the new amplitude of the SHM? (Take √2=1.41,√3=1.73) (Approximate to two decimals)
View SolutionA horizontal spring block system ( mass m_2 spring constant k) is oscillating on a smooth surface with amplitude A. If at the mean position an identical block is kept on it so that they move together after what is the new amplitude?
View SolutionA mass m, connected to a horizontal spring performs SHM with amplitude A. While mass m, is passing through mean position, another mass m, is placed on it so that both the masses move together with amplitude A,. The ratio of
View Solution
