A horizontal tube has different cross-sectional areas at point A and B .The diameter of A is 4 cm and that of B is 2 cm. Two manometer limbs are attached at A and B. When a liquid of density 8.0 g cm−3 flows through the tube, the pressure difference between the limbs of the manometer is 8 cm. Calculate the rate of flow of the liquid in the tube .
Step by step video solution for A horizontal tube has different cross-sectional areas at point A and B .The diameter of A is 4 cm and that of B is 2 cm. Two manometer limbs are attached at A and B. When a liquid of density 8.0 g cm^(-3) flows through the tube, the pressure difference between the limbs of the manometer is 8 cm. Calculate the rate of flow of the liquid in the tube . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
Similar Questions
The diameter of a horizontal tube at points A and B are 6 cm and 3 cm, respectively. Two manometer limbs are attached at A and B. When water is allowed to flow through the tube, pressure difference of 10 cm is noted between the limbs. Calculate the rate of flow of water in the tube.
View SolutionThe diameter of the throat of a venturimeter is 6 cm .when it is inserted in a horizontal pipe line of diameter 10 cm the pressure difference between the pipe and the thraot equal 8 cm of water . Calulate the rate of flow.
View Solution
Knowledge Check
The figure shown a pipe of uniform cross-section inclined in a vertical plane. A U-tube manometer is connected between the point A and B. If the liquid of density ρ0 flows with velocity v0 in the pipe. Then the reading h of the manometer is
 Ah=0Bh=v202gCh=ρ0ρ(v202g)Dh=ρ0Hρ−ρ0
Ah=0Bh=v202gCh=ρ0ρ(v202g)Dh=ρ0Hρ−ρ0A horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
Aa1a2√2gha21−a22Ba1a2√2gh(a21−a22)Ca1a2 ⎷(a21+a22)h2g(a21−a22)D2a1a2gh√a21−a22
Two capillary tubes of equal length and inner radii 2r and 4r respectively are added in series and a liquid flows through it. If the pressure difference between the ends of the whole system is 8.5 cm of mercury, find the pressure difference between the ends of the first capillary tube.
View SolutionA pitot tube is fixed in a water pipe of diameter 14cm and difference of pressure by the gauge is 20cm of water column. Calculate the rate of flow of water.
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View SolutionUnder a constant pressure head, the rate of streamlined volume flow of a liquid through a capillary tube is V. if the length of the capillary tube is double and diameter of the bore is halved, find the rate of flow of the liquid through the capillary tube.
View SolutionThe figure shows a siphon in action. The liquid flowing through the siphon has a density of 1.5gm/cm3. Calculate the pressure difference between
(a) Points A and D,
(b) Points B and C
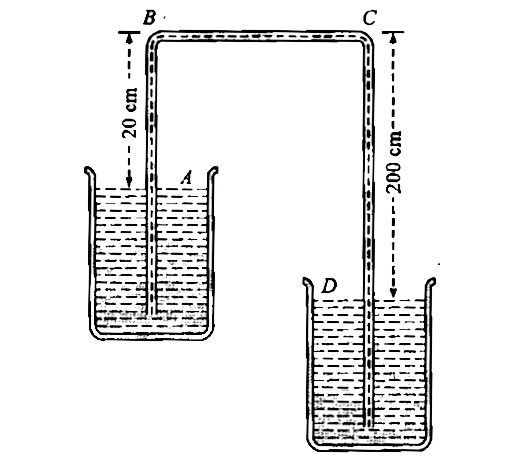
View Solution
