The ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
The speed of flow is minimum when the cross - sectional area of the tube is maximum . The equation foe minimum speed of flow of the liquid in a venturimeter is given as
v1=A2√2ρ0ghρ(A21−A22)=
⎷2(ρ0/ρ)gh(A1A2)2−1
Putting ρ0/ρ=η1,A1A2=πr21πr22=(r1r2)2=η2 ,
we obtain , v1=√2η1ghη4−1
Topper's Solved these Questions
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
10 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - SOLVED PROBLEMS (OBJECTIVE )
14 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
Similar Questions
The ratio of height of a mercury column in a barometer at a place to the height of the liquid column at the same place are 1:4. Find the density of the liquid.
View SolutionFigure shows a device called Pitot tube . It measures the velocity of moving fluids . Determine the velocity of the fluid in terms of the density ρ the density of the fluid in manometer (U-tube) σ and the height h .
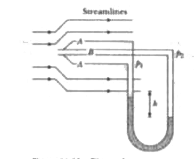
View Solution
Knowledge Check
A vertical U-tube contains a liquid of densityρ and surface tension T. if the radius of the meniscus of liquid in the limbs of the U-tube are R1 and R2 find the difference in the liquid column in the limbs.
AΔh=T(R1−R2)ρgR1R2BΔh=2T(R1−R2)ρgR1R2CΔh=2T(R1+R2)ρgR1R2DΔh=4T(R1−R2)ρgR1R2Water is flowing therough a tube of diameter 1 cm at 8 cm/s. Taking η=10−2 poise the flow of liquid and Reynold's number are
Astreamline, 80Bstreamline, 800Cstrbulent, 8000Dturblent, 9000If V1 and V2D be the volumes of the liquids flowing out of the same tube in the same interval of time and η1 and η2 their coefficients of viscosity respectively then
Aη1η2=V2V1Bη1η2=V1V2Cη1η2=V21V22Dη1η2=V22V21
A tube of length l and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The fluid flow velocity depends on the distance r from the axis of the tube as v=v0(1−r2/R2). Find:
(a) the volume of the fluid flowing across the section of the tube per unit time:
(b) the kinetic energy of the fluid within the tube's volume,
(c) the friction force exerted on the tube by the fluid,
(d) the pressure difference at the ends of the tube.
View SolutionA source moves away from an obeserver with a certain speed, and the ratio of actual to the apparent frequency as heard by the observer in η. If the two approach each other with the same speed, then find the ratio.
View SolutionA source moves away from an obeserver with a certain speed, and the ratio of actual to the apparent frequency as heard by the observer in η. If the two approach each other with the same speed, then find the ratio.
View SolutionA vertical steel rod has radius a. The rod has a coat of a liquid film on it. The liquid slides under gravity. It was found that the speed of liquid layer at radius r is given by
v=ρgb22ηln(ra)−ρg4η(r2−a2)
Where b is the outer radius of liquid film, η is coefficient of viscosity and ρ is density of the liquid.
(i) Calculate the force on unit length of the rod due to the viscous liquid?
(ii) Set up the integral to calculate the volume flow rate of the liquid down the rod. [you may not evaluate the integral]
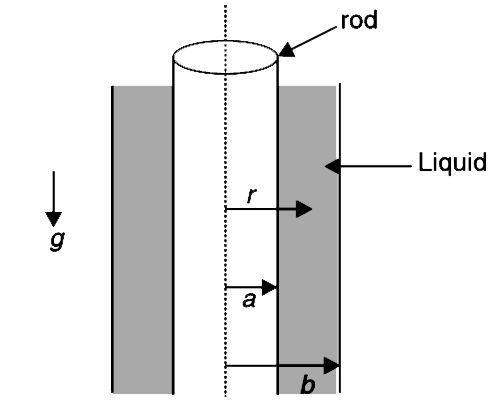
View SolutionShown in the figure is a container whose top and botoom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as ρ. Calculate the coefficient of viscosity η.
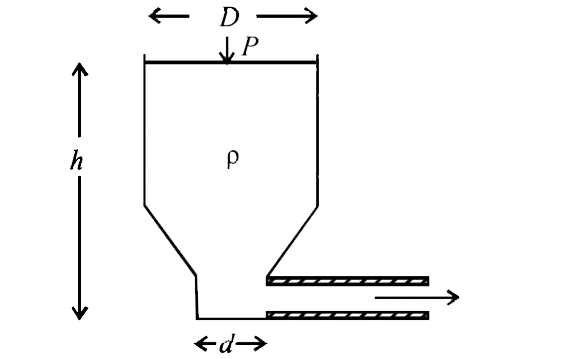
View Solution
