A hot body placed in a surrounding of temperature θ0 obeys Newton's law of cooling dθdt=−k(θ−θ0) . Its temperature at t=0 is θ1 the specific heat capacity of the body is s and its mass is m. Find (a) the maximum heat that the body can lose and (b) the time starting from t=0 in which it will lose 90% of this maximum heat.
The correct Answer is:A, B
Given :
Heat capacity =m×s=8−J^∘C
(dthηdt)∈creases=2∘Cs
(dthηdt)decreases=0.2∘Cs
(a) Powerofheater=mS(dthηdt)∈creases
=80×2=160W
(b) Power of radiated
=mS(dthηdt)+(decreases)
=80×0.2=16W.
(c) Now, m(dthη(dt)decreases=K(T−T0
⇒16=K(30−20)
⇒K+1610=1.6
Now (dthηdt)=K(T−T0)=1.6×(30−25)
=1.6×5=8W.
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Objective 2
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
A hot fbody placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will loss half the maximum heat it can lose.
View SolutionA hot body placed in air is cooled down according to newton's law of cooling the rate of decrease of temperature being k times the temperature difference from the surrounnding Starting from t=0 The time in which the body will lose half of the maximum heat is xLn22k Find the value of x .
View Solution
Knowledge Check
In Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
AA: surface of the bodyBS in the specific heat of the bodyC1m being the mass of the bodyDe is the emissivity of the bodyAccording to Newton’s law of cooling ms dθdt=−K(θ−θ0). If σ is Stefan’s constant, A is surface area of the body and T∘ is temperature of surroundings in K, then the value of K on the basis of Stefan-Boltzmann law is –
AσAT40BσAT30C4σAT40D4σAT30A body cools in a surrounding which is at a constant temperature of θ0 Assume that it obeys Newton's law of cooling Its temperature θ is plotted against time t Tangents are drawn to the curve at the points P(θ=θ1) and Q(θ=θ2) These tangents meet the time axis at angle of ϕ2 andϕ1 as shown
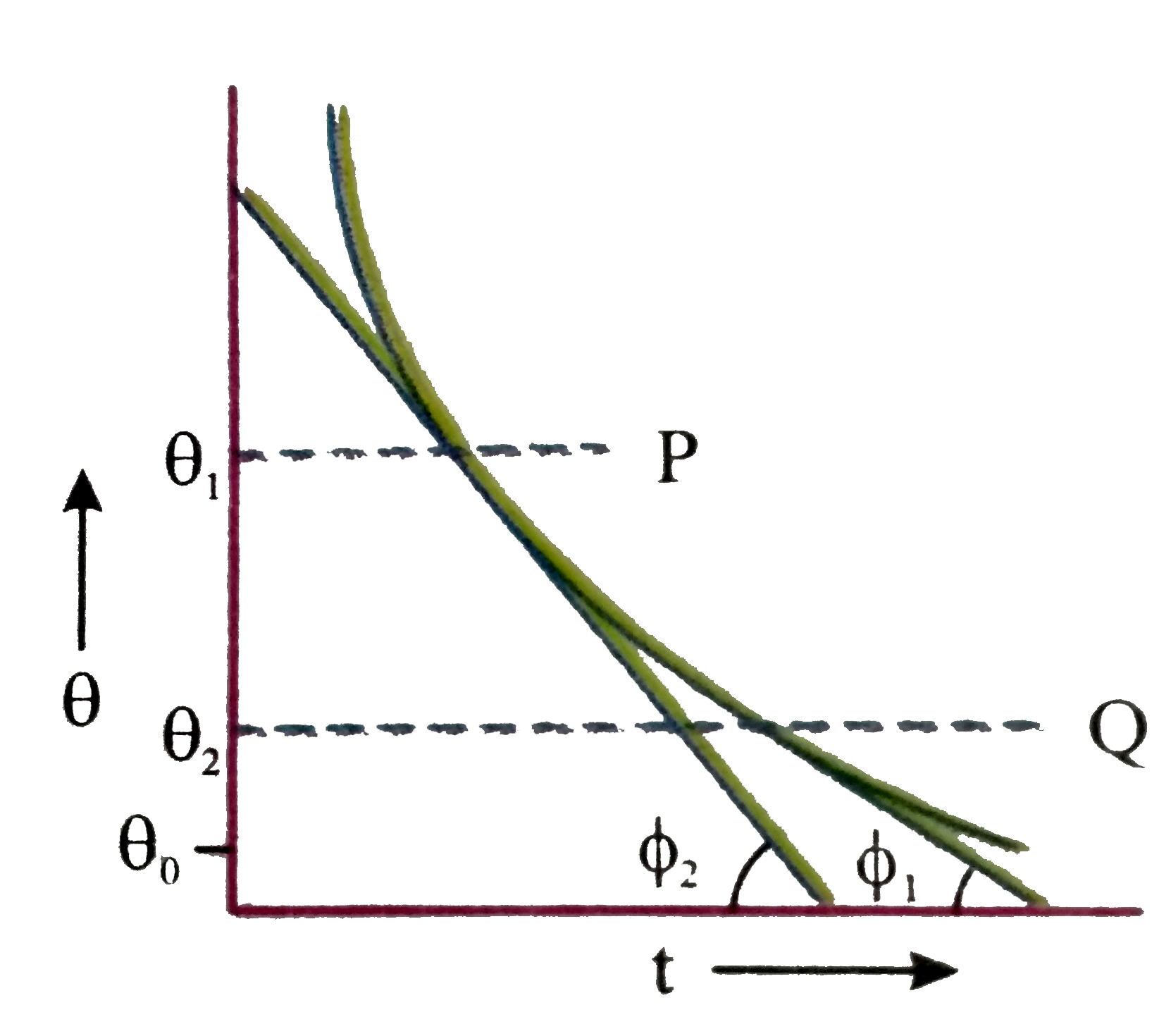 .Atanϕ2tanϕ1=θ1−θ0θ2−θ0Btanϕ2tanϕ1=θ1−θ0θ2−θ0Ctanϕ2tanϕ1=θ1−θ0θ2−θ0Dtanϕ2tanϕ1=θ1−θ0θ2−θ0
.Atanϕ2tanϕ1=θ1−θ0θ2−θ0Btanϕ2tanϕ1=θ1−θ0θ2−θ0Ctanϕ2tanϕ1=θ1−θ0θ2−θ0Dtanϕ2tanϕ1=θ1−θ0θ2−θ0
In Newton's law of cooling experiment, we plot a graph of (dθdt) against the temperature difference (θ−θ0). The graph is
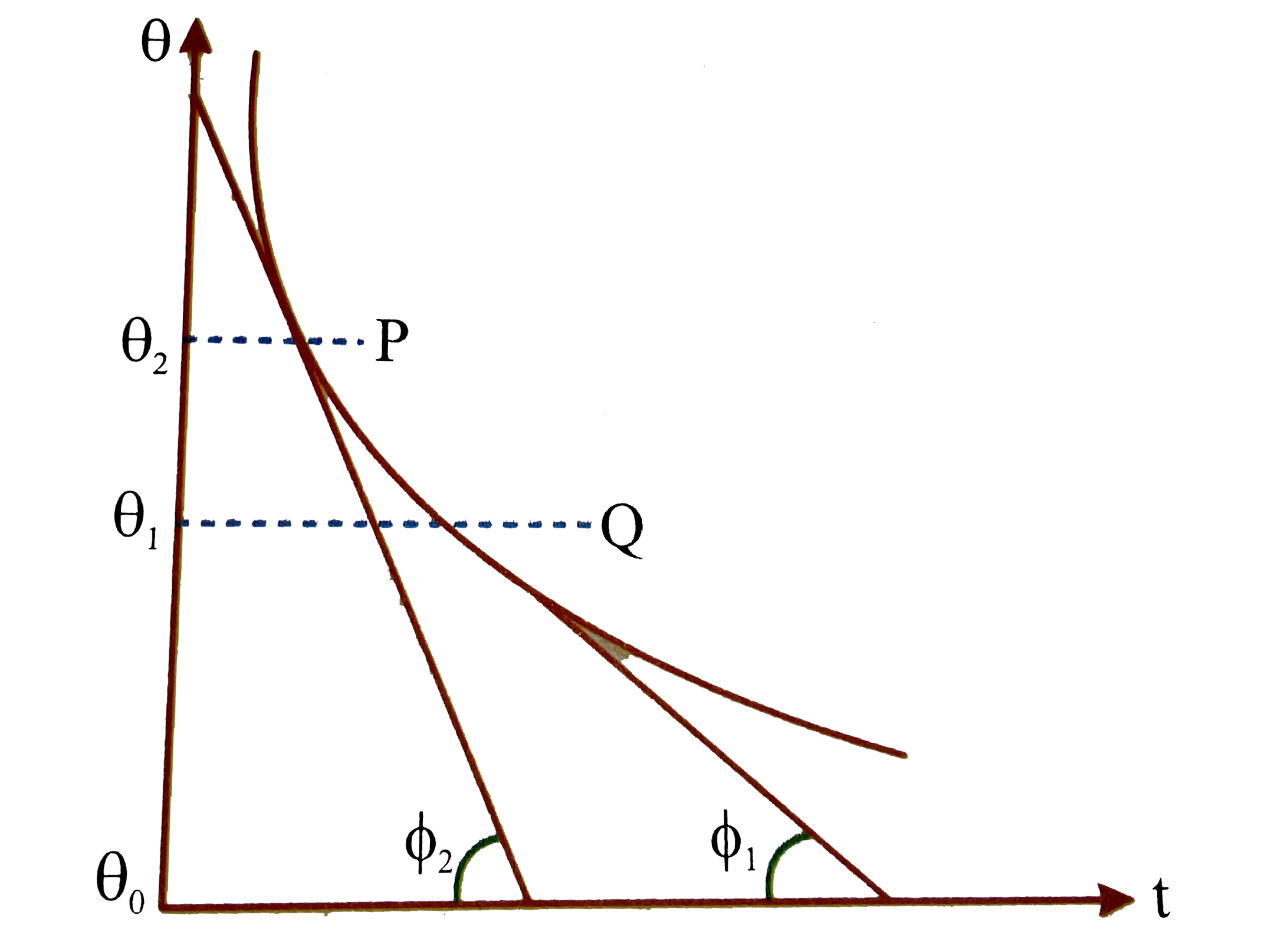
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newyon's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
View SolutionWhen a body is placed in surroundings at a constant temperature of 20∘C and heated by a 10W heater, its temperature remains constant at 40∘C. If the temperature of the body is now raised from 20∘C to 80∘C in 5 min at a uniform rate, the total heat it will lose to the surroundings will be
View SolutionIf the temperature of the body θ and time of cooling 't' and room temperature of the surrounding θ0. The cooling curve is
View SolutionA body at temperature θ0 having Newton's cooling constant K is placed in a surrounding having temperature T0 at time t = 0. The graph of temperature of the body as a function of time t is shown in the adjacent figure. A tangent on the curve is drawn at t = 0 as shown in the figure. Find the value of τ.

View Solution
