A body at temperature θ0 having Newton's cooling constant K is placed in a surrounding having temperature T0 at time t = 0. The graph of temperature of the body as a function of time t is shown in the adjacent figure. A tangent on the curve is drawn at t = 0 as shown in the figure. Find the value of τ.

K
1K
K(Q0−T0)
Data insufficient
The correct Answer is:B
mgsinθ−fS=maC.M.
(fs)R=(25mR2)α
⇒fs=25maC.M
⇒mgsinθ=75maC.M⇒aC.M=57gsinθ
For time of descent
12aC.Mt2=hcosecθ
t2=2haC.Mcosecθ
t2=2h×75gsinθcosecθ
t2=14h5g1sin2θ⇒t=√14h5g1sinθ&VF=(aC.M)t=(57gsina)(√14h5g)1sinθ
VF=√5×2gh7=√10gh7 implies Velocity does not depend or 'θ' but time depend on 'θ'

Topper's Solved these Questions
Similar Questions
Knowledge Check
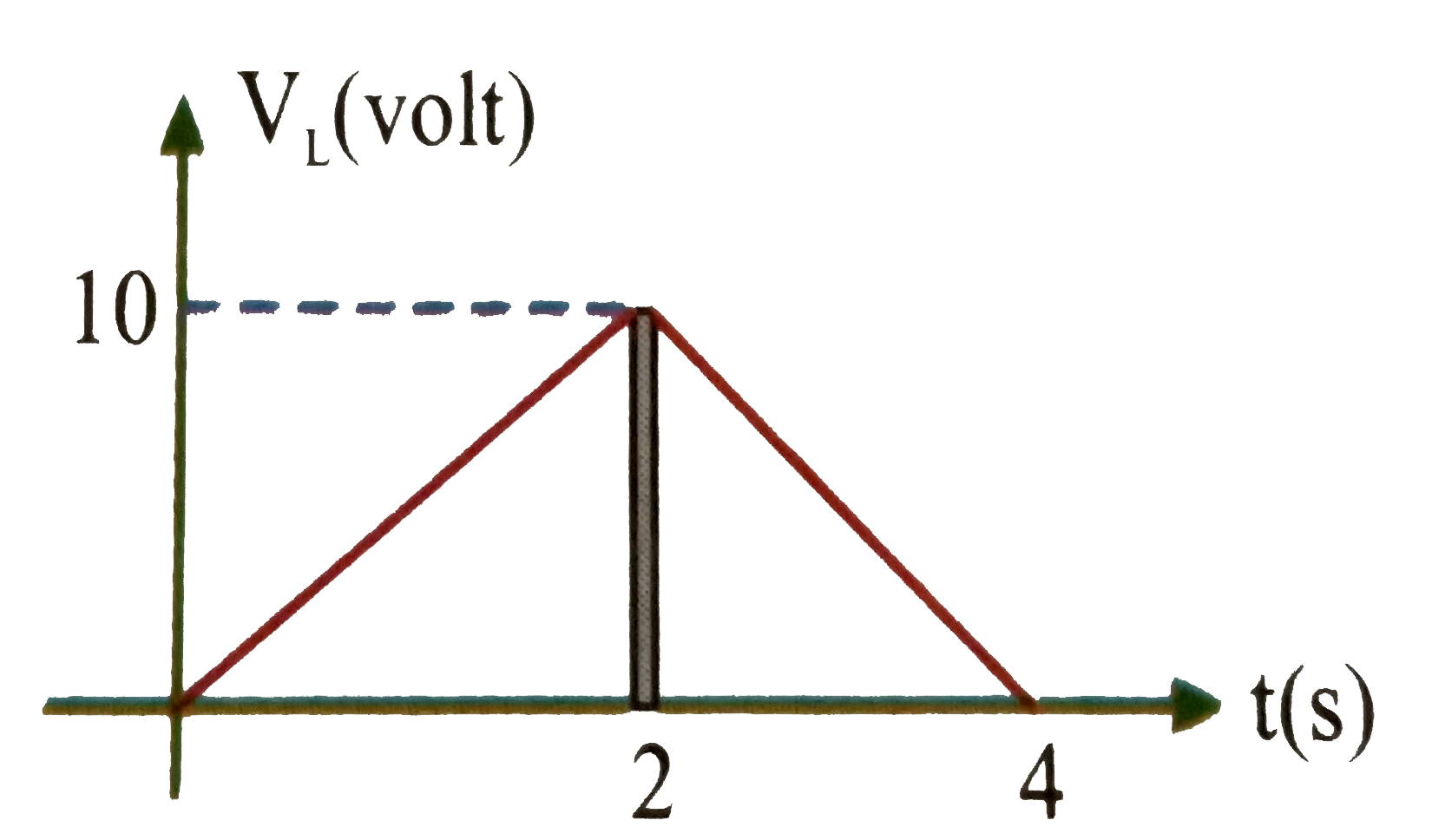
The potential difference across a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current t=2 second is
 A1AB3AC4AD5A
A1AB3AC4AD5AThe potential difference a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current versus time graph across the inductor will beA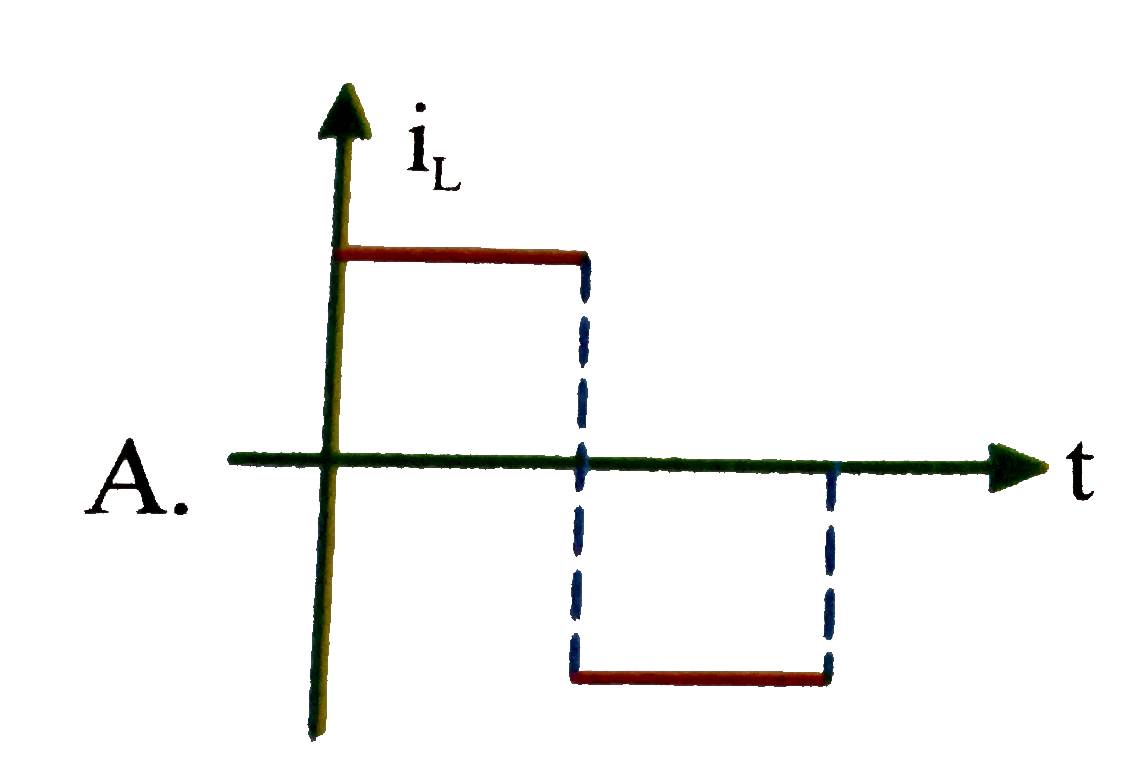 B
B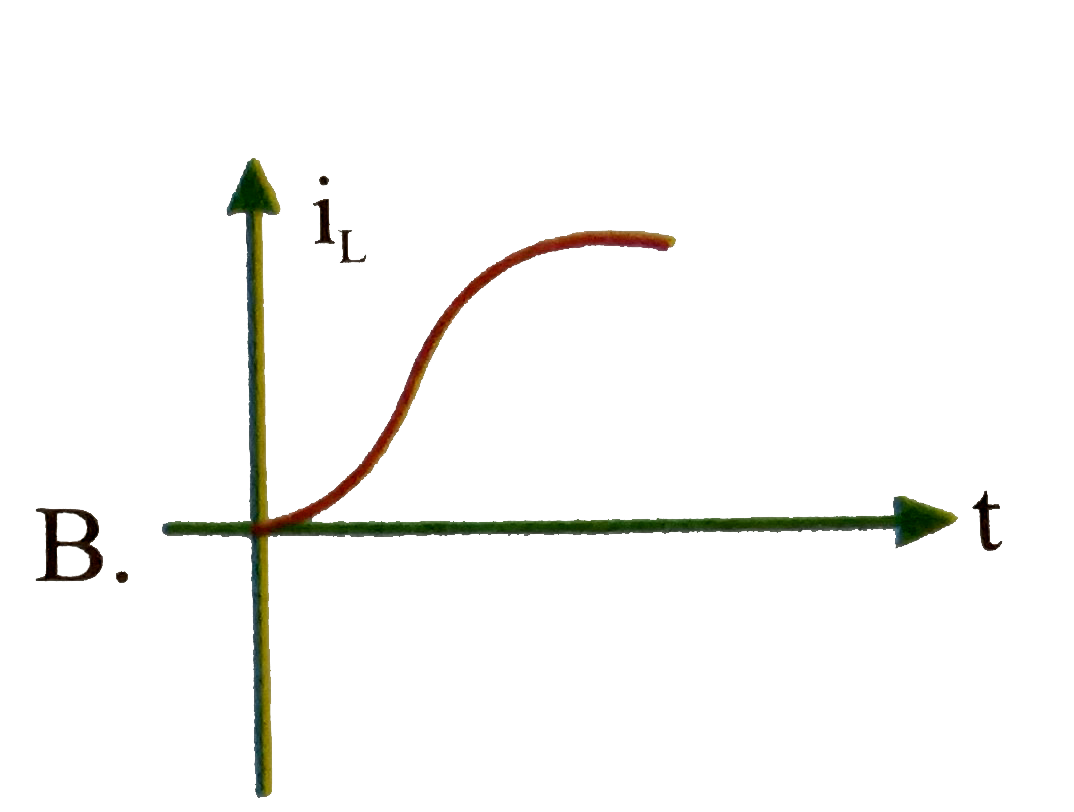 C
C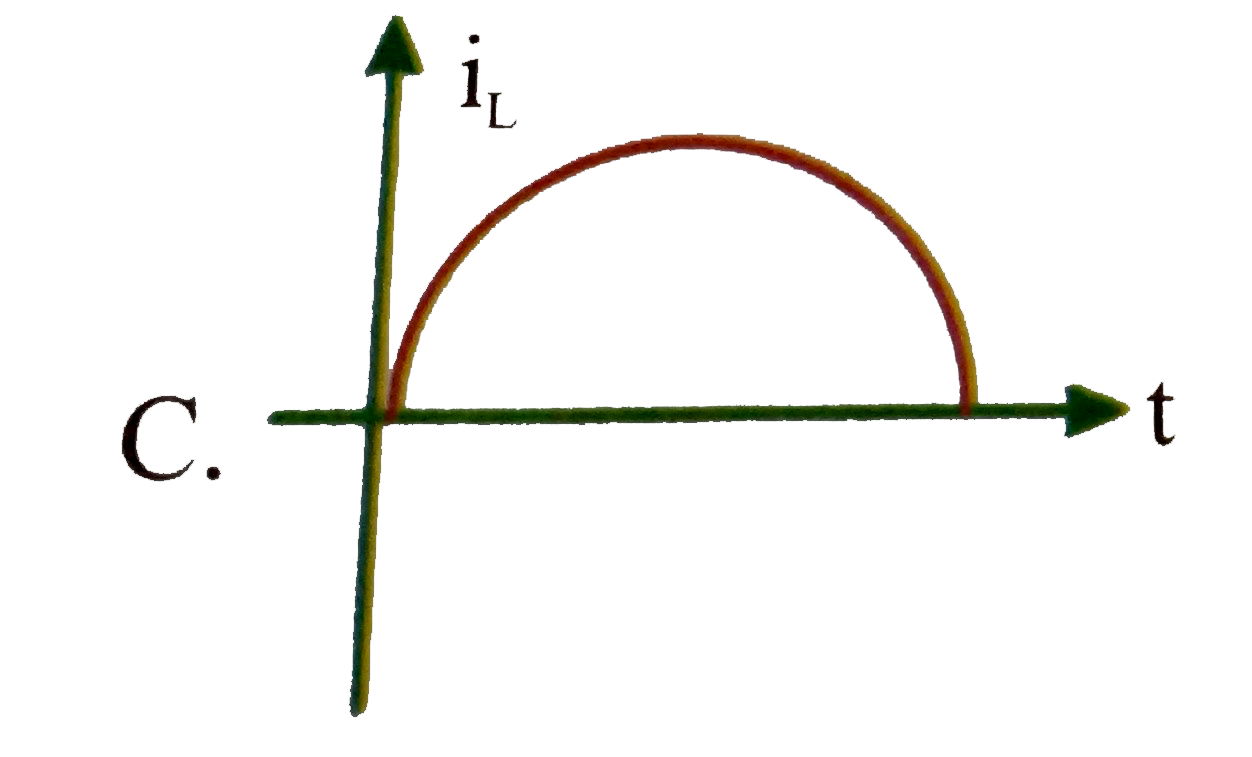 D
D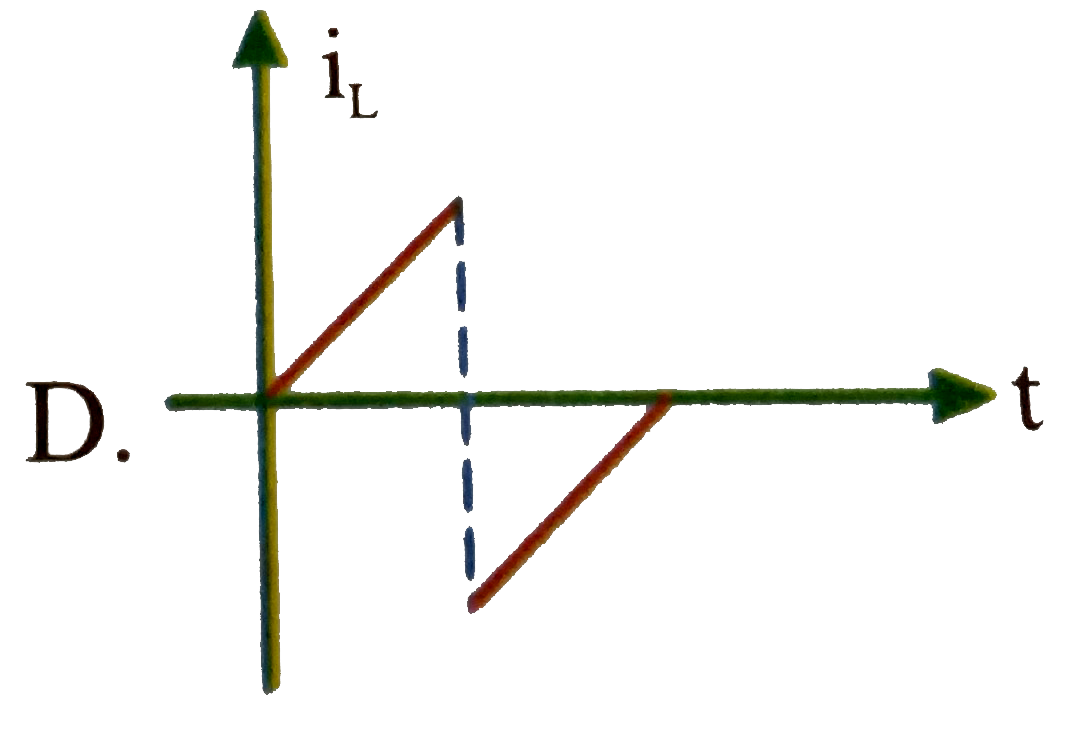
For the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
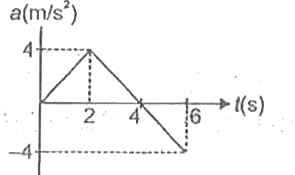 A10 m/sB4 m/sC12 m/sD8 m/s
A10 m/sB4 m/sC12 m/sD8 m/s
If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View SolutionThe dependence of the acceleration of a body with time is shown in Figure. At t=0, the velocity of the body is −3m/s and position is x=0m.

View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionThe temperature of an isolated black body falls from T1 to T2 in time t. Let c be a constant
View SolutionThe velocity time graph of a body moving along a straight line is shown in figure. The ratio of the average velocities during the time t1 and t2 is.
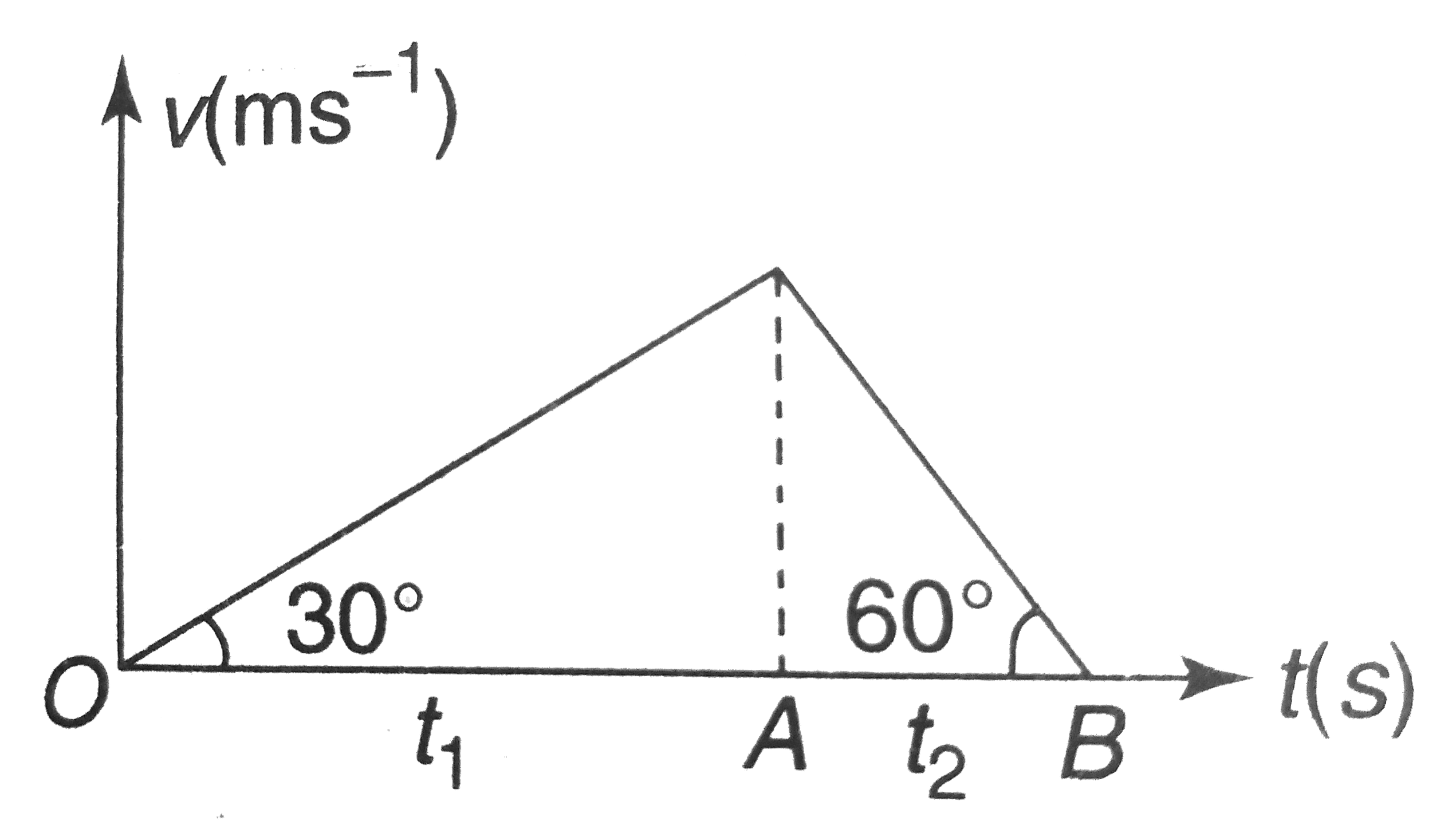
View Solution

