A junction diode is connected to an external resistance of 100Ω and a source of e.m.f. 3.0V. If potential barrier developed in the junction diode is 0.7, obtain the current in the circuit.
To solve the problem, we will follow these steps:
Step 1: Understand the circuit
We have a junction diode connected to an external resistance (R) of 100 ohms and a source of electromotive force (e.m.f) of 3.0V. The potential barrier (V_b) of the diode is given as 0.7V.
Step 2: Apply Kirchhoff's Voltage Law (KVL)
According to KVL, the sum of the potential differences (voltage) around a closed loop must equal zero. In our circuit, we can write the equation as:
e.m.f−Potential barrier−Voltage across the resistor=0
Substituting the known values:
3.0V−0.7V−I⋅100Ω=0
Step 3: Rearrange the equation to find current (I)
Rearranging the equation gives us:
I⋅100Ω=3.0V−0.7V
I⋅100Ω=2.3V
Step 4: Solve for current (I)
Now, we can solve for the current (I):
I=2.3V100Ω
I=0.023A
To convert this to milliamperes (mA), we multiply by 1000:
I=23mA
Final Answer
The current in the circuit is 23 mA.
---
We have a junction diode connected to an external resistance (R) of 100 ohms and a source of electromotive force (e.m.f) of 3.0V. The potential barrier (V_b) of the diode is given as 0.7V.
According to KVL, the sum of the potential differences (voltage) around a closed loop must equal zero. In our circuit, we can write the equation as:
e.m.f−Potential barrier−Voltage across the resistor=0
Substituting the known values:
3.0V−0.7V−I⋅100Ω=0
Rearranging the equation gives us:
I⋅100Ω=3.0V−0.7V
I⋅100Ω=2.3V
Now, we can solve for the current (I):
I=2.3V100Ω
I=0.023A
To convert this to milliamperes (mA), we multiply by 1000:
I=23mA
The current in the circuit is 23 mA.
Topper's Solved these Questions
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - Problems (LEVEL-II)
9 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXAMPLES
56 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - Exercise (very Short answer questions)
36 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
60 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
Similar Questions
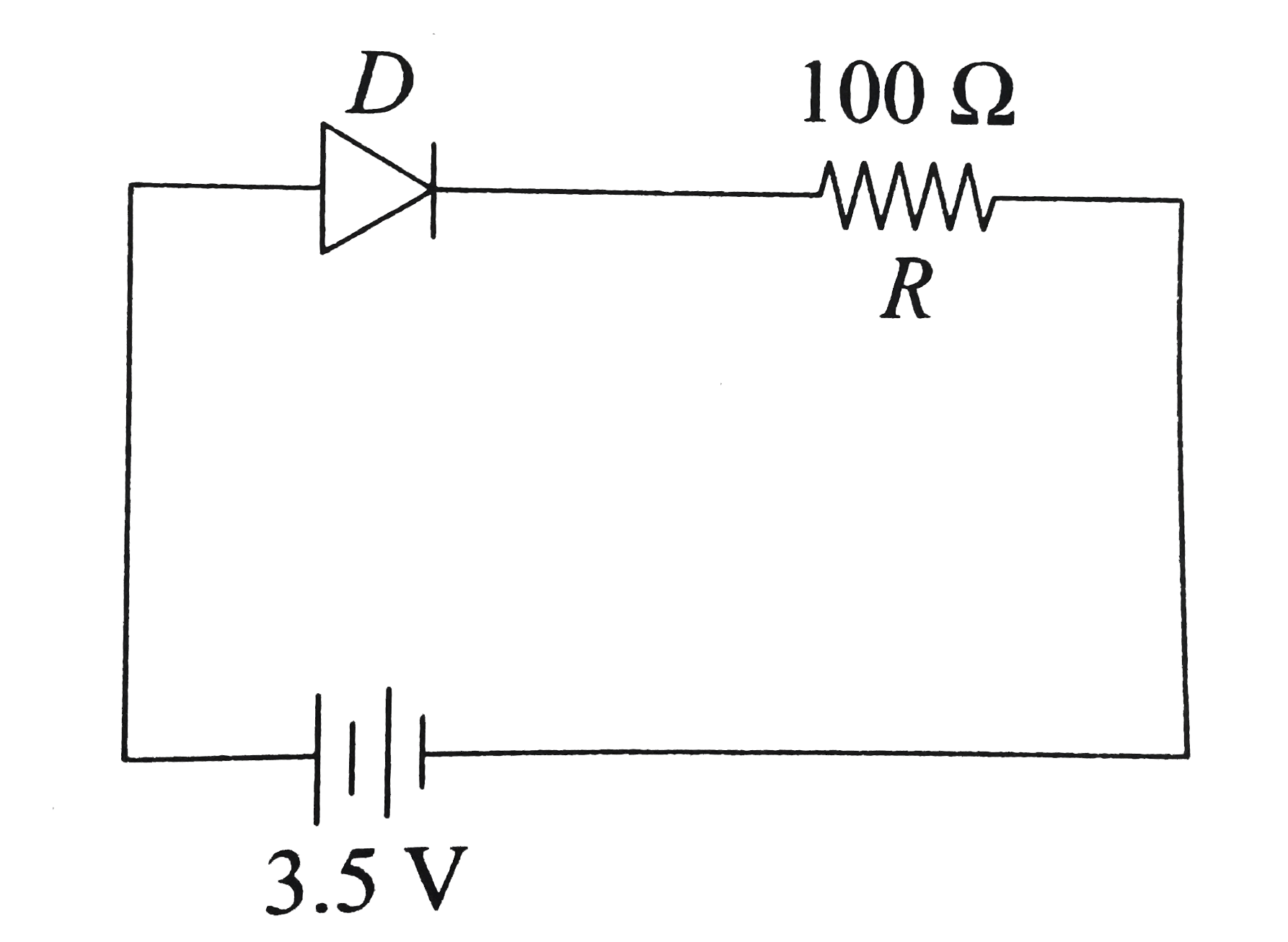
In the given figure, a diode D is connected to an external resistance R=100Ω and an emf of 3.5V. If the barrier potential developed across the diode is 0.5V, the current in the circuit will be :
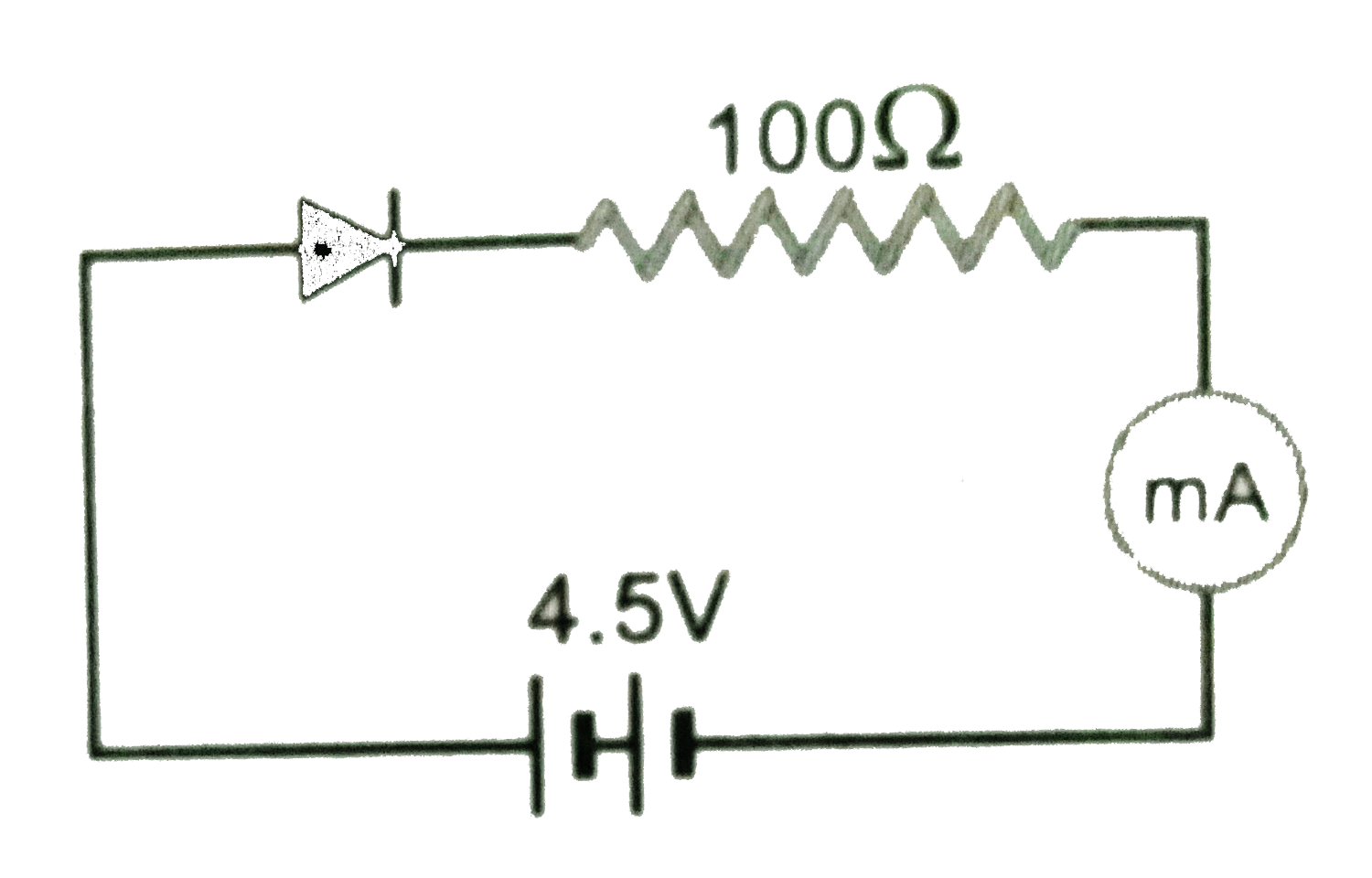
View SolutionFigure Shows a diode connected to an external resistance and an e.m.f. Assuming that the barrier potential developed in diode is 0.5V, obtain the value of current in the circuit in milliampere.
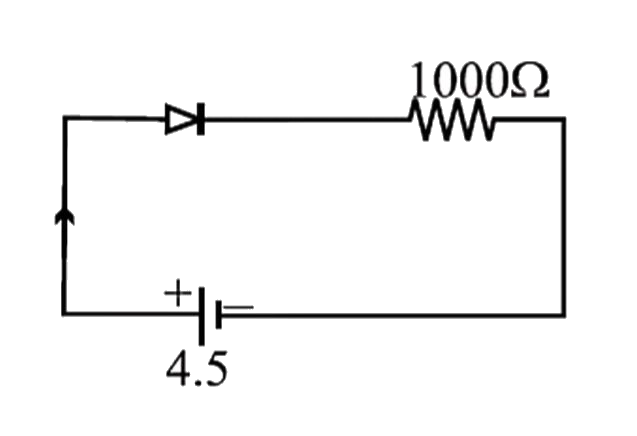
View SolutionA P-N junction diode connected to a battery of e.m.f. 4.5 V and an external resistance of 1000Ω. What is the value of current in the circuit, if potential barrier in the diode =0.5V
View SolutionA p-n junction in series with a resistance of 5kΩ is connected across a 50 V DC source . If the forward bias resistance of the junction is 50Ω , the forward bias current is
View SolutionA cell of e.m.f. ε and internal resistance r sends a current of 1.0 A when it is connected to an external resistance of 1.9 Ω. But it sends a current of 0.5 A when it is connected to an resistance of 3.9Ω calculate the values of ε and r .
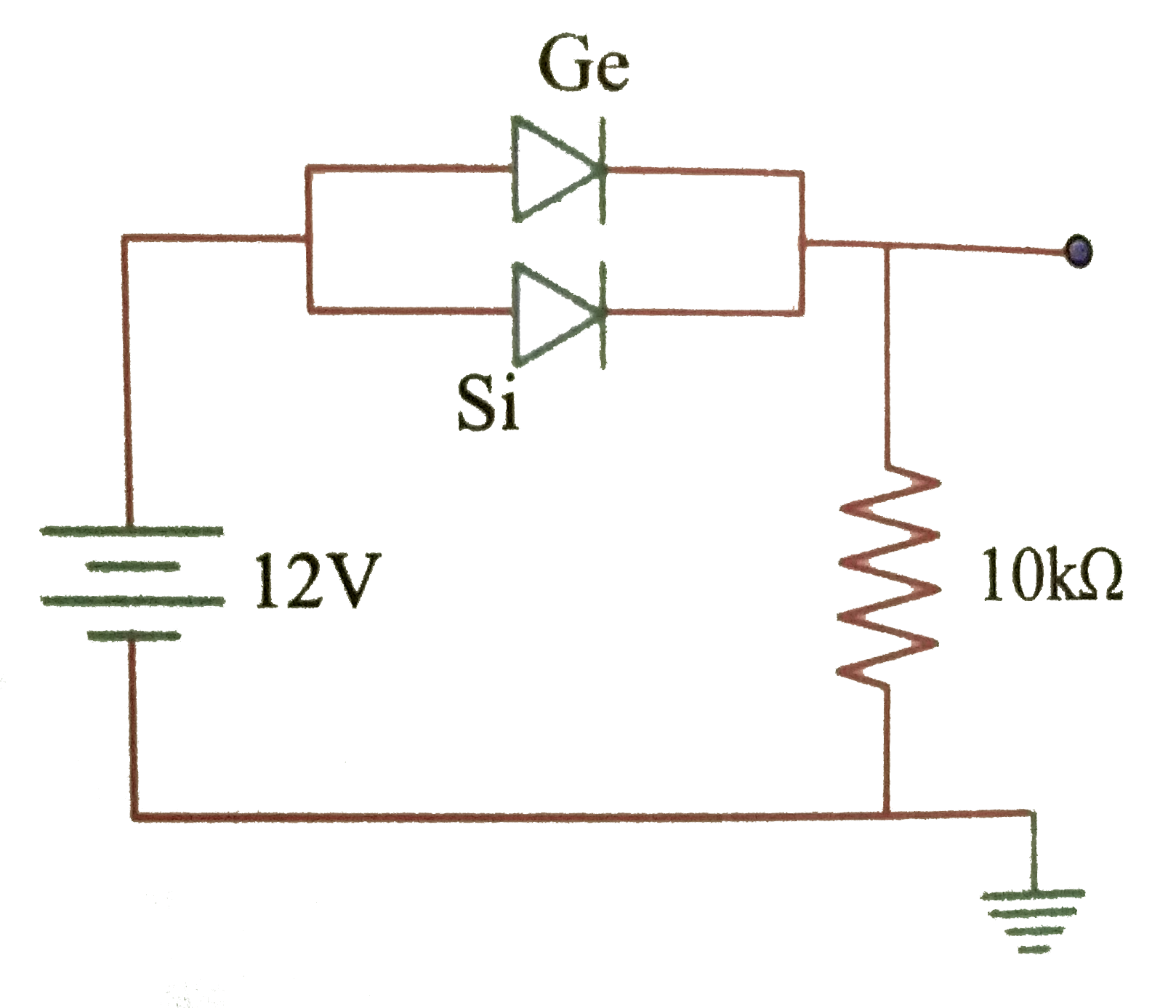
View SolutionTwo junction diodes, one of germanium (Ge) and other of silicon (Si) are connected as shown in fig to a battery of 12V and a load resistance 10kΩ. The germanium diode conducts at 0.3V and silicon diode at 0.7V. When current flows in the circuit, the potential of terminal Y will be
 .
.
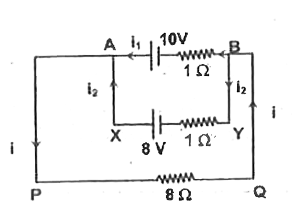
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionThe circuit shown in the figure contains two diodes each with a forward resistance of 50Ω and with infinite backward resistance. If the batter of 6 V is connected in the circuit, then the current through the 100Ω resistance is
View SolutionTwo cells having emf's of 10 V and 8 V, respectively, are connected in series with a resistance of 24Ω In the external circuit. Their internal resistances are 2Ω/V (proportional to their emf's). Find the current in the circuit

View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View Solution
