A cell of e.m.f. ε and internal resistance r sends a current of 1.0 A when it is connected to an external resistance of 1.9 Ω. But it sends a current of 0.5 A when it is connected to an resistance of 3.9Ω calculate the values of ε and r .
To solve the problem, we need to apply Ohm's Law and the concept of internal resistance in a circuit. Let's break down the solution step by step.
Step 1: Understand the Circuit
We have a cell with an electromotive force (e.m.f.) denoted as E and an internal resistance denoted as r. The cell is connected to an external resistor R.
Step 2: Set Up the Equations
We are given two scenarios:
1. When the external resistance R1=1.9Ω, the current I1=1.0A.
2. When the external resistance R2=3.9Ω, the current I2=0.5A.
Using Ohm's Law, the total resistance in the circuit can be expressed as:
Rtotal=R+r
The current flowing through the circuit can be expressed as:
I=ERtotal=ER+r
Step 3: Write the Equations for Each Case
For the first case:
I1=ER1+r⟹1.0=E1.9+r
This can be rearranged to:
E=1.0×(1.9+r)⟹E=1.9+r(Equation 1)
For the second case:
I2=ER2+r⟹0.5=E3.9+r
This can be rearranged to:
E=0.5×(3.9+r)⟹E=1.95+0.5r(Equation 2)
Step 4: Equate the Two Expressions for E
Now we have two expressions for E:
1. E=1.9+r
2. E=1.95+0.5r
Setting these equal to each other:
1.9+r=1.95+0.5r
Step 5: Solve for r
Rearranging the equation:
r−0.5r=1.95−1.9
0.5r=0.05
r=0.050.5=0.1Ω
Step 6: Substitute r Back to Find E
Now substitute r=0.1Ω back into Equation 1 to find E:
E=1.9+0.1=2.0V
Final Answer
The values are:
- E=2.0V
- r=0.1Ω
We have a cell with an electromotive force (e.m.f.) denoted as E and an internal resistance denoted as r. The cell is connected to an external resistor R.
We are given two scenarios:
1. When the external resistance R1=1.9Ω, the current I1=1.0A.
2. When the external resistance R2=3.9Ω, the current I2=0.5A.
Rtotal=R+r
The current flowing through the circuit can be expressed as:
I=ERtotal=ER+r
For the first case:
I1=ER1+r⟹1.0=E1.9+r
This can be rearranged to:
E=1.0×(1.9+r)⟹E=1.9+r(Equation 1)
I2=ER2+r⟹0.5=E3.9+r
This can be rearranged to:
E=0.5×(3.9+r)⟹E=1.95+0.5r(Equation 2)
Now we have two expressions for E:
1. E=1.9+r
2. E=1.95+0.5r
1.9+r=1.95+0.5r
Rearranging the equation:
r−0.5r=1.95−1.9
0.5r=0.05
r=0.050.5=0.1Ω
Now substitute r=0.1Ω back into Equation 1 to find E:
E=1.9+0.1=2.0V
The values are:
- E=2.0V
- r=0.1Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C) MULTIPLE CHOICE TYPE)
2 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
A cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionThe resistance of 0.1 N solution of acetic acid is 250 ohm whne measured ina cell of cell constant 250 ohm whne measured in acell of cell constant 1.15 cm−1 The equivalent conductance (inohm−1cm2equivalent−1) of 0.1 N acetic acid is
View SolutionThe internal resistance of primary cell is 4Ω it genrater a current of 0.2A and connected to a external resistance 0f '21Omega' in which resistance connected is providing the the heat per second is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
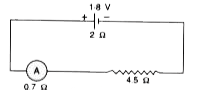
What would be the reading of the ammeter ?
View SolutionA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View Solution
