Three identical cells, each of emf 2 V and internal resistance are connected in series to an external resistor of . Calculate the current in the circuit.
To solve the problem of finding the current in a circuit with three identical cells connected in series, we can follow these steps:
Step 1: Determine the Net EMF
Since we have three identical cells, each with an EMF of 2 V, we can calculate the total EMF (E_net) of the circuit by adding the EMFs of all three cells:
Enet=E1+E2+E3=2V+2V+2V=6V
Step 2: Calculate the Total Internal Resistance
Each cell has an internal resistance of 0.2 Ω. Since the cells are connected in series, the total internal resistance (R_internal) is the sum of the internal resistances of each cell:
Rinternal=r1+r2+r3=0.2Ω+0.2Ω+0.2Ω=0.6Ω
Step 3: Identify the External Resistance
The external resistor (R_external) is given as 7.4 Ω.
Step 4: Calculate the Total Resistance in the Circuit
The total resistance (R_total) in the circuit is the sum of the total internal resistance and the external resistance:
Rtotal=Rinternal+Rexternal=0.6Ω+7.4Ω=8.0Ω
Step 5: Calculate the Current Using Ohm's Law
Using Ohm's Law, we can find the current (I) in the circuit:
I=EnetRtotal=6V8.0Ω=0.75A
Final Answer
The current in the circuit is 0.75 A.
---
Since we have three identical cells, each with an EMF of 2 V, we can calculate the total EMF (E_net) of the circuit by adding the EMFs of all three cells:
Each cell has an internal resistance of 0.2 Ω. Since the cells are connected in series, the total internal resistance (R_internal) is the sum of the internal resistances of each cell:
The external resistor (R_external) is given as 7.4 Ω.
The total resistance (R_total) in the circuit is the sum of the total internal resistance and the external resistance:
Using Ohm's Law, we can find the current (I) in the circuit:
The current in the circuit is 0.75 A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-6
5 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-3
4 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThree identical cells each of emf 2 V and internal resistance 1Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6Ω Find the current delivered by the battery.
View SolutionA set of 4 cell each of emf 2V and internal resistance 1.5Ω are connected across an external load of 10Ω with 2 rows, two cells in each row. Calculate the current in each row and potential difference across 10Ω
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
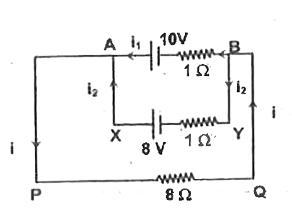
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View SolutionThree identical cells , each having an emf1.5V and a constant internal resistance 2.0ohm, are connected in series with a 4.0ohm resistor R, first as in circuit (i) , and second as in circuit (ii) . Then
( power in R in circuit (i))/( Power in R in circuit (ii)) =

View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
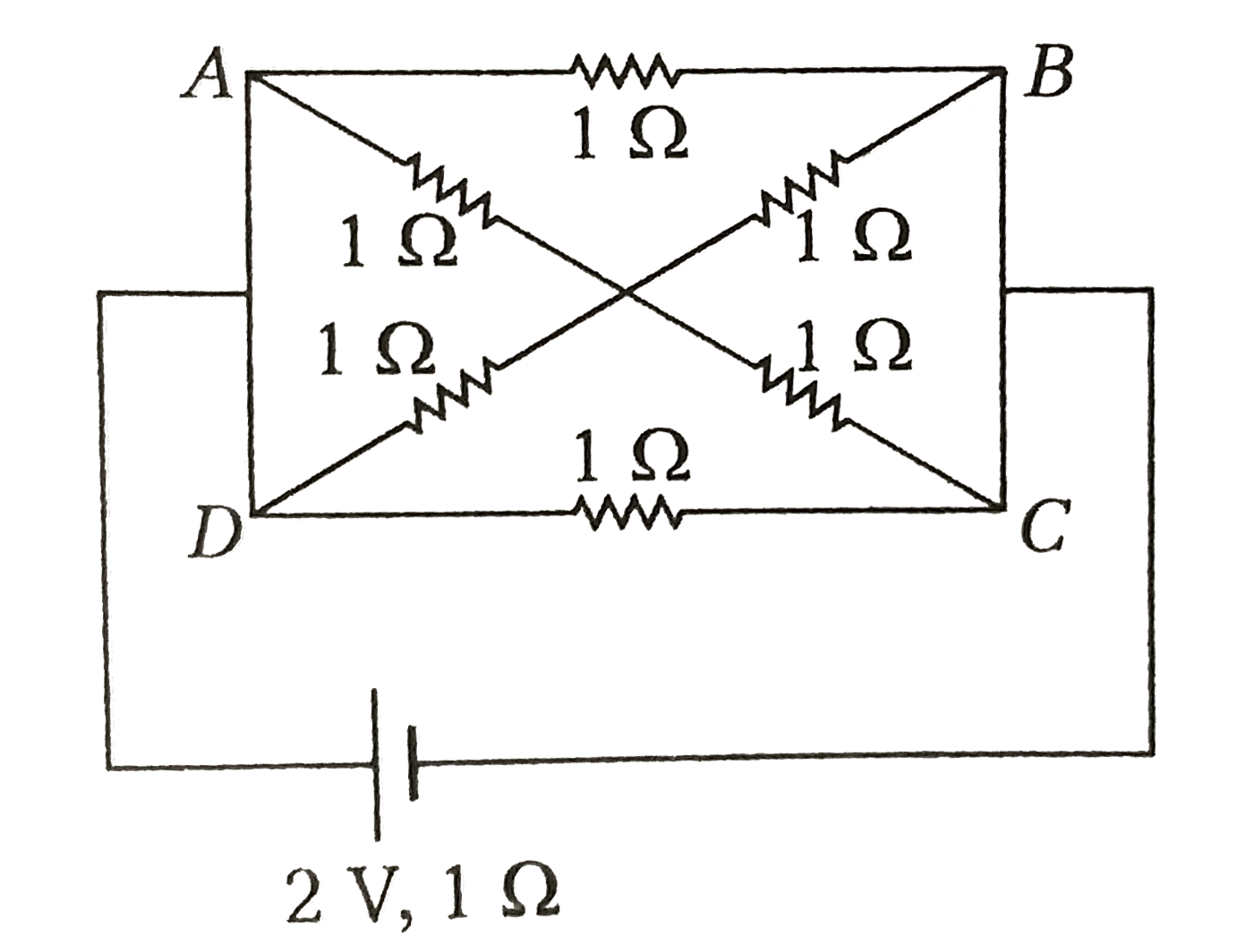
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
View SolutionTen cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View Solution
