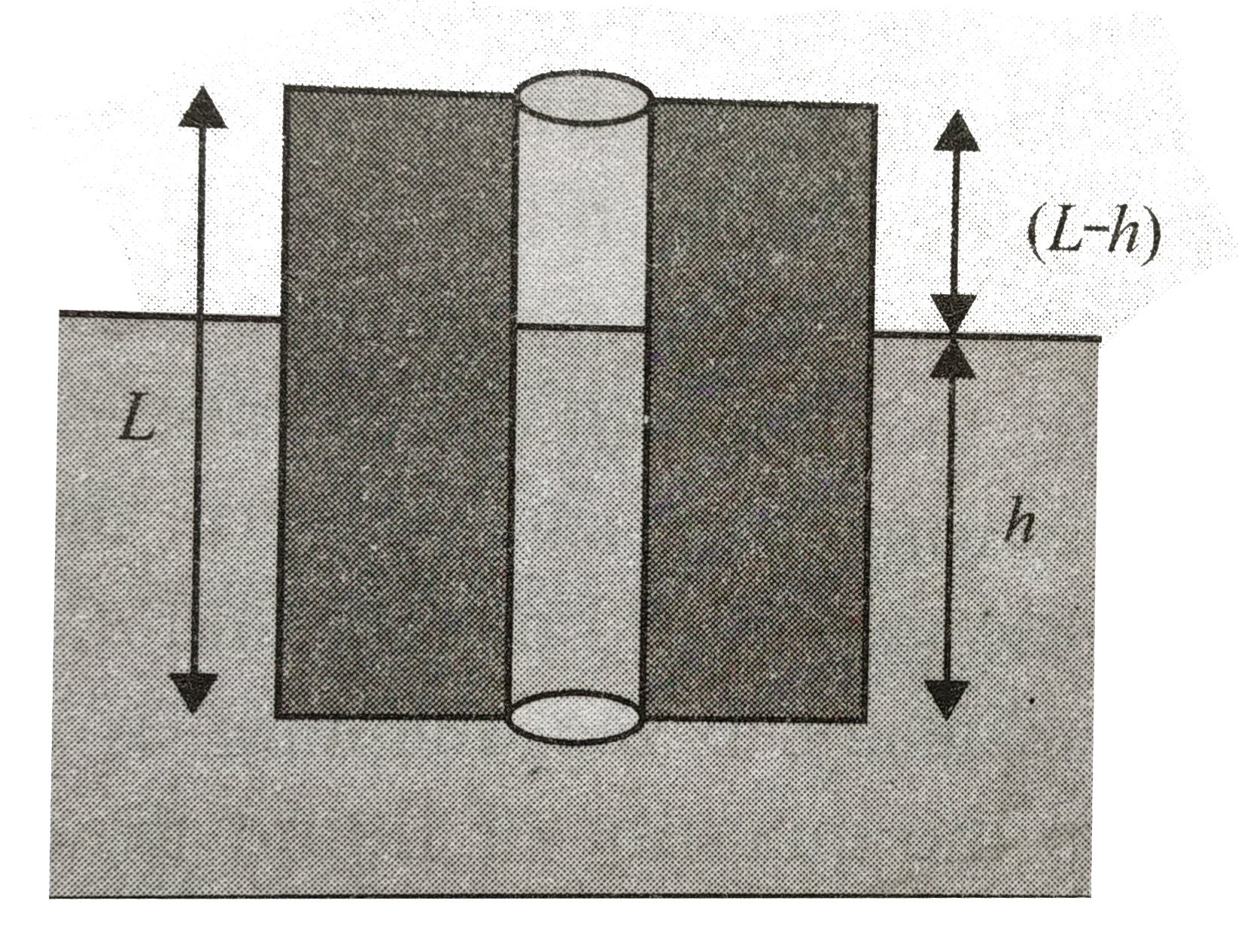
A large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum length of the rope required to scoop out a bucket full of water through the hole is . Find the value of . Take density of ice
The correct Answer is:5
To solve the problem, we need to find the value of x given that the minimum length of the rope required to scoop out a bucket full of water through a hole in a block of ice is (0.2×x) meters. The block of ice is 10 cm thick and has a density of 0.9 g/cm³.
1. Understand the Problem:
We have a block of ice floating in water with a hole drilled through it. The thickness of the ice is 10 cm. We need to find the length of the rope required to scoop water through this hole.
2. Identify the Forces:
The block of ice is floating, which means the weight of the ice is balanced by the buoyant force (upthrust) acting on it.
3. Set Up the Equation:
Let y be the height of the water level inside the hole. The volume of the submerged part of the ice can be expressed as:
Vsubmerged=A⋅(10−y)
where A is the cross-sectional area of the hole.
4. Calculate the Weight of the Ice:
The weight of the ice is given by:
Wice=Vice⋅ρice⋅g=A⋅10⋅0.9⋅g
5. Calculate the Buoyant Force:
The buoyant force is equal to the weight of the water displaced by the submerged part of the ice:
Fbuoyant=Vsubmerged⋅ρwater⋅g=A⋅(10−y)⋅1⋅g
6. Set the Forces Equal:
Since the ice is floating, we set the weight of the ice equal to the buoyant force:
A⋅10⋅0.9⋅g=A⋅(10−y)⋅1⋅g
7. Cancel Out Common Terms:
We can cancel A and g from both sides:
10⋅0.9=10−y
8. Solve for y:
Rearranging gives:
y=10−9=1 cm
9. Relate y to the Length of the Rope:
The minimum length of the rope required to scoop out water through the hole is given as 0.2x meters. Since y=1 cm, we convert this to meters:
y=0.01 m
Therefore, the length of the rope is:
0.2x=0.01⟹x=0.010.2=0.05 m
10. Convert to Required Units:
Since the problem states x in meters, we need to express x in terms of the required value:
x=5 m
Final Answer:
The value of x is 5.
We have a block of ice floating in water with a hole drilled through it. The thickness of the ice is 10 cm. We need to find the length of the rope required to scoop water through this hole.
The block of ice is floating, which means the weight of the ice is balanced by the buoyant force (upthrust) acting on it.
Let y be the height of the water level inside the hole. The volume of the submerged part of the ice can be expressed as:
Vsubmerged=A⋅(10−y)
where A is the cross-sectional area of the hole.
The weight of the ice is given by:
Wice=Vice⋅ρice⋅g=A⋅10⋅0.9⋅g
The buoyant force is equal to the weight of the water displaced by the submerged part of the ice:
Fbuoyant=Vsubmerged⋅ρwater⋅g=A⋅(10−y)⋅1⋅g
Since the ice is floating, we set the weight of the ice equal to the buoyant force:
A⋅10⋅0.9⋅g=A⋅(10−y)⋅1⋅g
We can cancel A and g from both sides:
10⋅0.9=10−y
Rearranging gives:
y=10−9=1 cm
The minimum length of the rope required to scoop out water through the hole is given as 0.2x meters. Since y=1 cm, we convert this to meters:
y=0.01 m
Therefore, the length of the rope is:
0.2x=0.01⟹x=0.010.2=0.05 m
Since the problem states x in meters, we need to express x in terms of the required value:
x=5 m
The value of x is 5.
Topper's Solved these Questions
Similar Questions
A large block of ice 5m thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice =0.9.
View SolutionIn the middle of a pond, a large ice block of 10 m thickness of floating. Let a vertical hole is drilled in this block. The minimum length (in cm) of a rope required to lift a bucket full of water through the hole is x×10cm? (Specify gravity of ice =0.91).
View Solution
Knowledge Check
A large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum of water through the hole is (density of ice =0.9gcm−3)
A0.5 mB1.0 mC1.2 mD1.8 mA large block of ice 4 m thick has a vertical hole drilled through it and is floating in the middle of water in a lake. The minimum length of rope required to scoop up a bucket full of the through the hole is (density of ice =0.9CGS unit, density of water =1CGS unit)
A40 cmB24 cmC20 cmD360 cmA large block of ice cuboid of edge length 'l' and density ρice−0.9ρw, has a larger vertical hole along its axis. This block is floating in a lake. Find out length of the rope required to raise a bucket of water through the hole.
Al/2Bl/4Cl/8Dl/10
A large block of ice cuboid of height 'l' and density ρice=0.9ρw' has a large vertical hole along its axis. This block is floating in a lake. Find out the length of the rope required to raise a bucket of water through the hole.
View SolutionA body weight 20 N in water and 30 N in air. Find the density of the body. Take the density of water as 1.0gcm−3.
View SolutionA body weight 20 N in water and 30 N in air. Find the density of the body. Take the density of water as 1.0gcm−3.
View SolutionA cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take π2=10 and g=10m/s2)
View SolutionThe thickness of the ice layer on the surface of lake is 20 m. A hole is made in the ice layer. What is the minimum length of the rope required to take a bucket full of water out ? (Take density of ice =0.9×103kg/m3)
View Solution
