A large rectangular box moves vertically downward with an acceleration a. A toy gun fixed at A and aimed towards C fires a particle P.

P will hit C if a=g
P will hit the roof BC, if a>g
P will hit the CD if a<g
May be either (a), (b) or (c) depending on the speed of projection of P.
The correct Answer is:D
Step by step video & image solution for A large rectangular box moves vertically downward with an acceleration a. A toy gun fixed at A and aimed towards C fires a particle P. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE
23 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - COMPREHENSION_TYPE
13 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
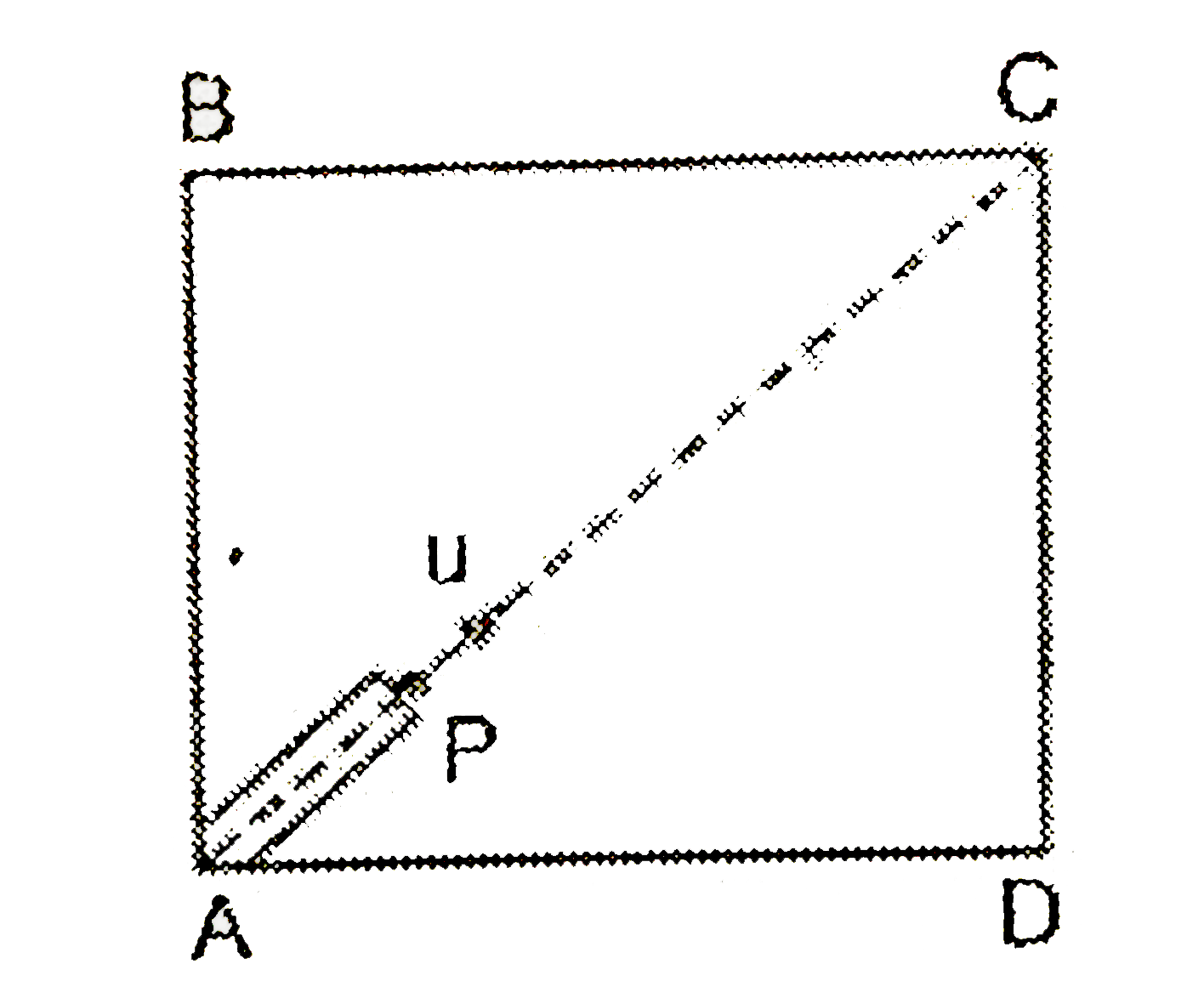
A large rectangular box ABCD falls vertically with an acceleration a. a toy gun fixed at A and aimed towards C fired a particle P.
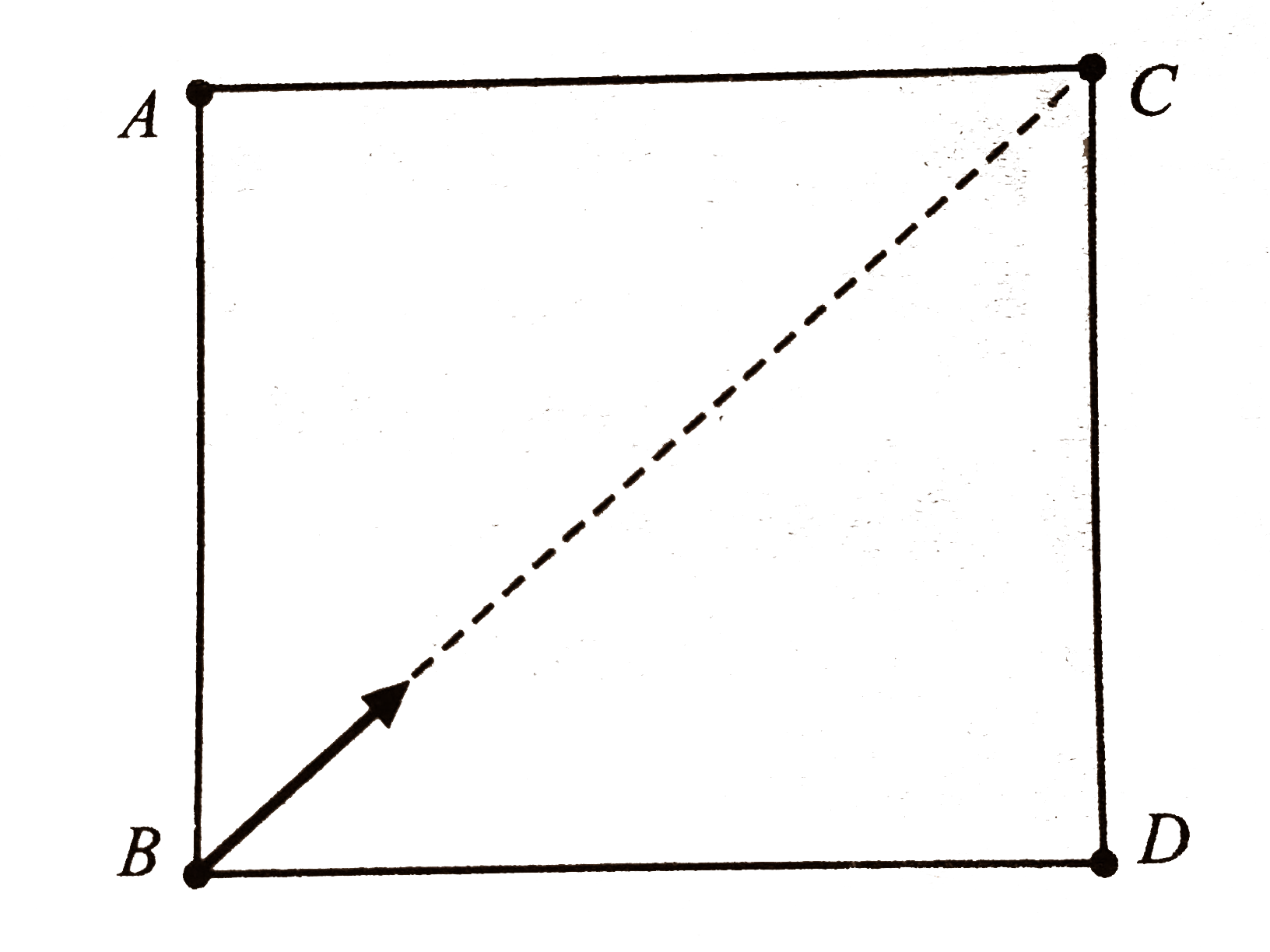
View Solution(Figure 5.196) shows an elevator cabin, which is moving downwards with constant acceleration a . A particle is projected from corner A, directly towards diagonally opposite corner C. Then prove that
(a) particle will hit C only when a=g.
(b) Particle will hit the wall CDifa<g.
( c) Particle will hit the roof BCifa>g.
 .
.
View Solution
Knowledge Check
Assuming all the surface to be frictionless. The smaller block m is moving horizontally with acceleration a and vertically downwards with acceleration a. Then magnitude of net acceleration of smaller block m with respect to ground
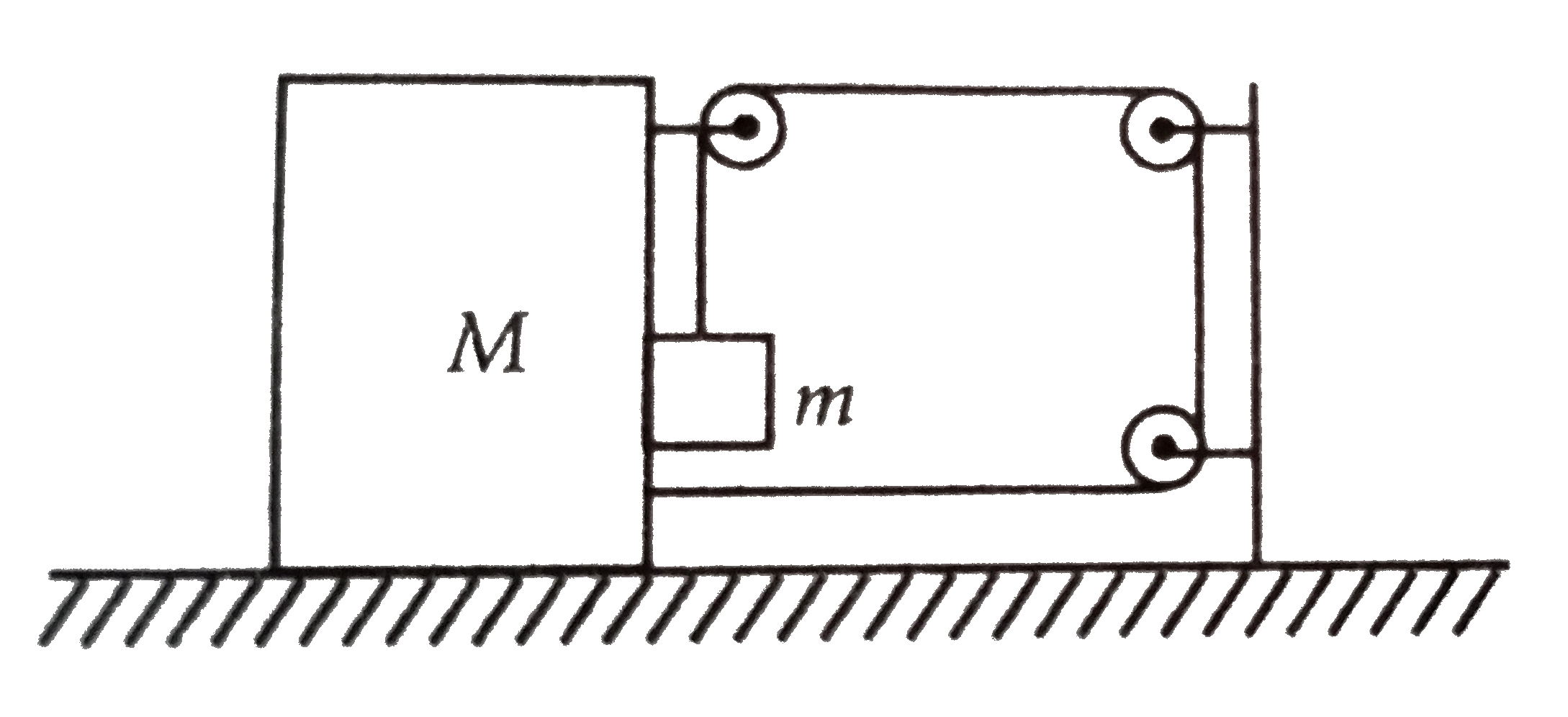 A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
A rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View SolutionFind the period of oscillation of a pendulum of length l if its point of suspension is
(a) moving vertically up with acceleration a
(b) moving vertically down with acceleration a(<g)
(c) failing freely under gravity
moving horizontal with acceleration a.
View SolutionA block of mass m is resting inside a smooth horizontal tube. If the tube accelerates vertically downward with acceleration a=kt where k is a positive constant, the correct plot showing the variation of normal reaction received by the block as a function of time (considering that upward direction of normal reaction is positive and taken towards positive direction y axis) will be

View SolutionA large box is moving on a horizontal floor with constant acceleration a=g. A particle is projected inside box with velocity u and angle θ with horizontal from box frame. For the given u, the value of θ for which horizontal range inside he box will be maximum is

View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .

View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View Solution
