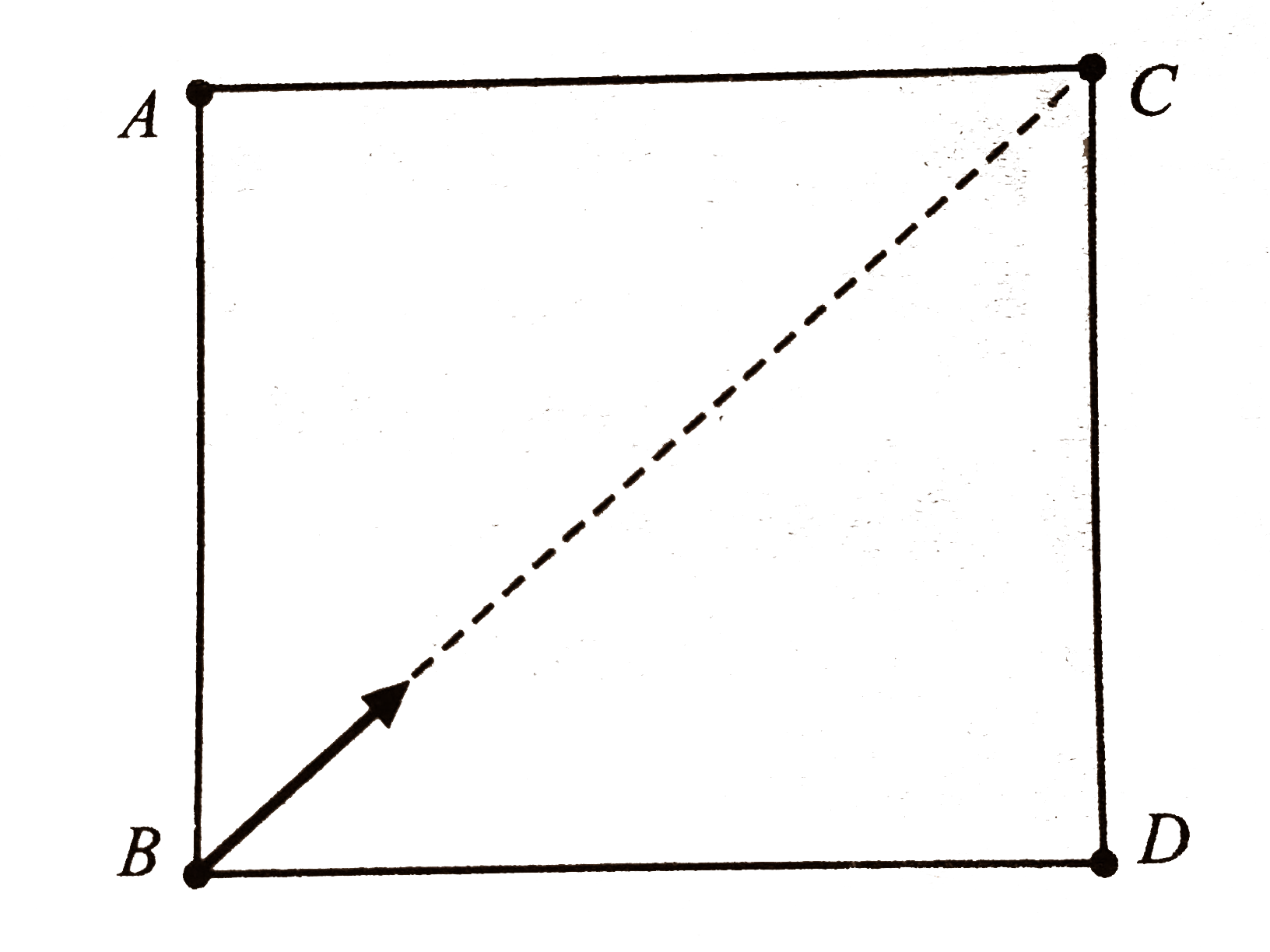
(Figure 5.196) shows an elevator cabin, which is moving downwards with constant acceleration a . A particle is projected from corner A, directly towards diagonally opposite corner C. Then prove that
(a) particle will hit C only when a=g.
(b) Particle will hit the wall CDifa<g.
( c) Particle will hit the roof BCifa>g.
 .
.
Superimpose an upward acceleration a on the system. The box becomes stationary. The particle has an upward acceleration a and a downward acceleration g.Ifa=g, the particle has no acceleration and will hit C. If a>g, the particle has a net upward acceleration, and if a<g, the particle has a net downward accleration.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A large box is moving on a horizontal floor with constant acceleration a=g. A particle is projected inside box with velocity u and angle θ with horizontal from box frame. For the given u, the value of θ for which horizontal range inside he box will be maximum is

View SolutionA particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :

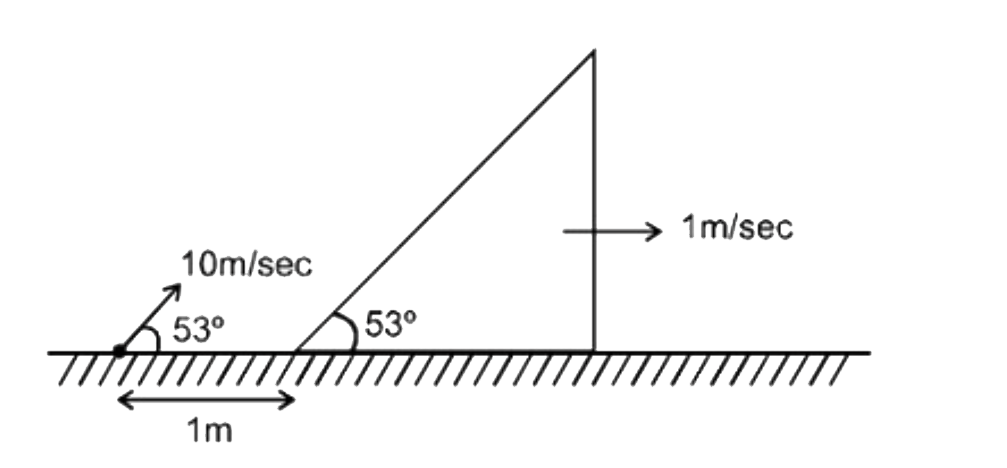
View SolutionA particle is projected from the ground and simultaneously a wedge starts moving towards the right, as shown in the figure. The maximum height of the wedge for which the particle will not hit the wedge is [g=10ms−2]
View SolutionWhat is the fractional decrease in the value of free-fall acceleration g for a particle when it is lifted from the surface to an elevation h? (h<<R)
View SolutionA particle is projected vertically upwards with velocity 40m/s. Find the displacement and distance travelled by the particle in
(a) 2s (b) 4s (c) 6s Take g=10m/s2
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
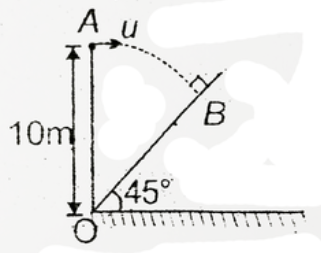
Find horizontal speed with which the particle was projected
View SolutionA particle is projected horizontally with spee u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
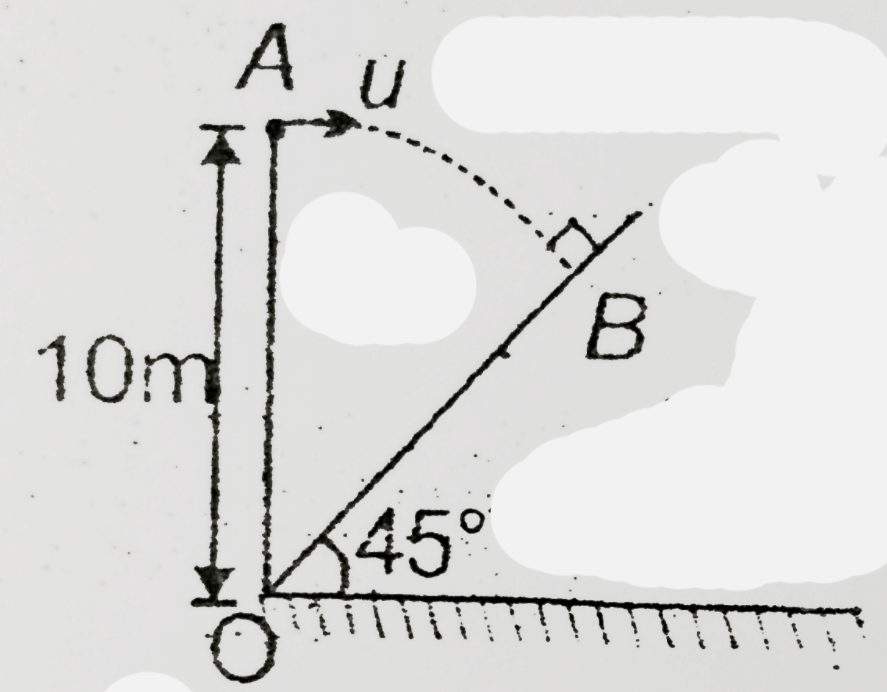
Find the length OB along the inclined plane
View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
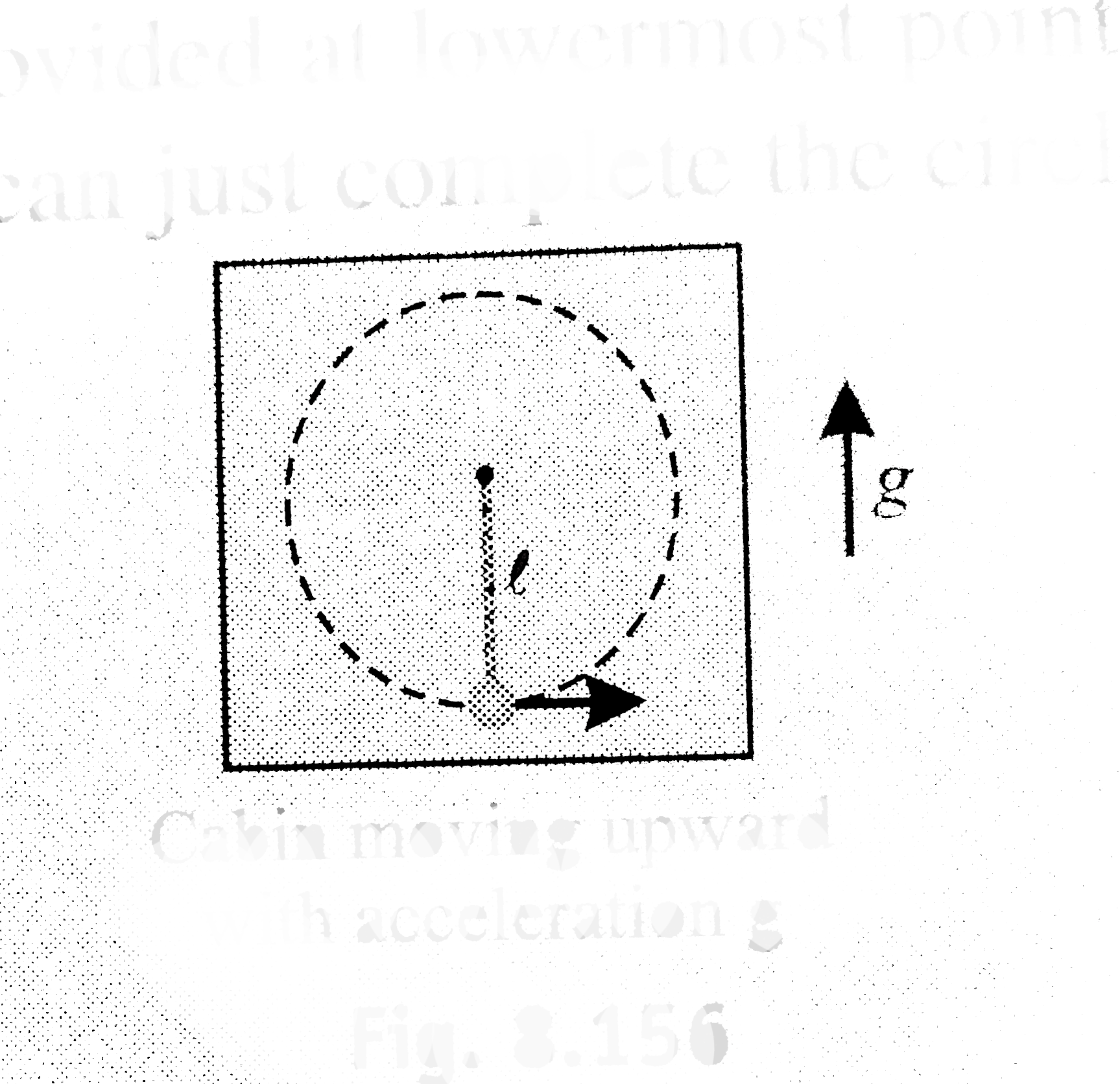
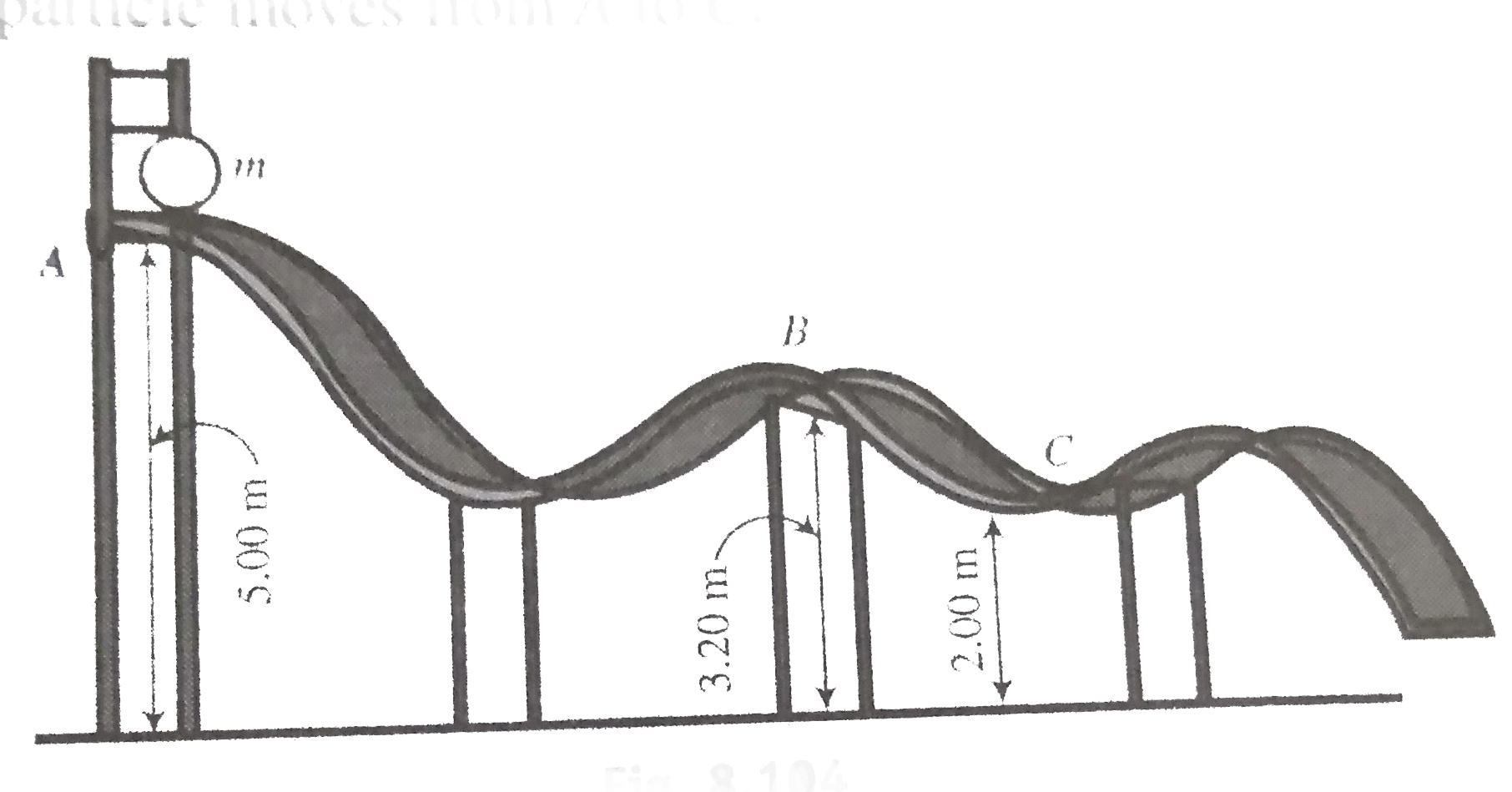
View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
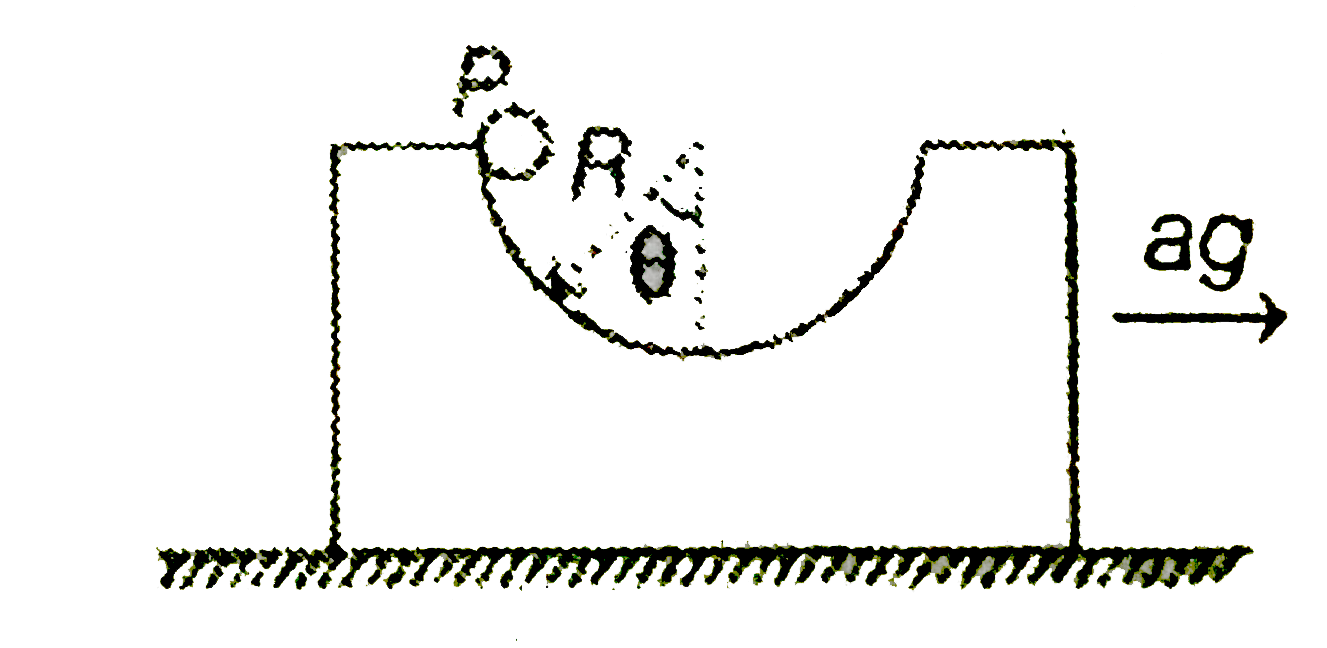
View SolutionInside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
View Solution
