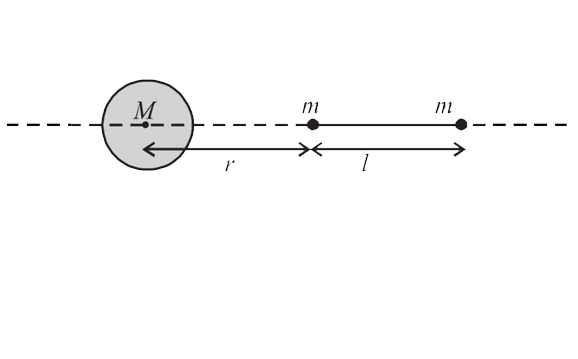
A larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only through their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tension in the rod is zero for m=k(M288). The value of k is
5
6
7
8
The correct Answer is:C
( c) Both the point masses are connected by a light rod so they have same acceleration.
Suppose each point mass is moving with acceleration a towards larger mass M.
Using Newton's 2nd law of motion for point mass nearer to larger mass,
F1−F=ma
GMm(3l)2−Gm2l2=ma ....(i)

Again using 2nd law of motion for another mass F2+F=ma
GMm(4l)2−Gm2l2=ma ....(ii)
From eqn. (i) and (ii), we get
GM9l2−Gml2=GM16l2+Gml2
M9−M16=m+m⇒7M144=2m
m=7M288=k(M288)∴k=7
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - NCERT Exemplar
8 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason
15 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Question
11 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View Solution
Knowledge Check
Two particles of masses m1 and m2 are connected to a rigid massless rod of length r to constitute a dumb bell which is free to move in the plane. The moment of inertia of the dumb bell about an axis perpendicular to the plane passing through the centre of mass is
Am1m2r2m1+m2B(m1+m2)r2Cm1m2r2m1−m2D(m1−m2)r2Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)A point mass is placed at a distance a from one end of a rod of mass M and length l on the line which passes through the central axis of the rod. The potential energy of the system.
AU=−GMmaloge(a+1a)BU=−GMm(1a−1a+1)CU=−GMm1loge(a+1a)DU=−GMma
Two particles of masses m and 2m are placed at separation L. Find the M.I. about an axis passing through the center of mass and perpendicular to the line joining the point masses.
View SolutionTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View SolutionMoment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
View SolutionTwo masses 'M' and '4M' are at a distance 'r' apart on the line joining them. 'P' is point where the resultant gravitational force is zero (such a point is called as null point). The distance of 'P' from the mass '4M' is
View Solution
