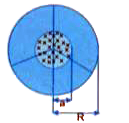
A line charge $λ$ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.08). A uniform magnetic field extends over a circular region within the rim. It is given by,
$\vec{B} = - B_{0} \hat{k} (r \leq a, a I t R)$
= 0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?

Text Solution

Verified by Experts

If the magnetic field changes with time, then,
Induced emf $ɛ = - \frac{d ϕ}{d t}$
This implies the presence of an electric field $v c e E$ tangential to all points of the periphery of the circular region denoted by a. If we move a test charge $q ɛ$ round this periphery a work qe will be done once round it. The electric force on the test charge is q E and the work done by this force round this periphery is $(q E) (2 π a)$ . Equating the two values of work done, we have
$q ɛ = (q E) (2 π a) \Rightarrow E = \frac{ɛ}{2 π a}$
Substituting the value of $ɛ$ , we get
$E = - \frac{1}{2 π a} \frac{d ϕ_{B}}{d t} = - \frac{a}{2} \frac{d B}{d t} [∴ ϕ_{B} = B A = π a^{2} B]$
In the given problem, the total charge on the rim $q = λ .2 π a$
Therefore, force on this charge $F = q E = - (λ .2 π a) (\frac{a}{2} \frac{d B}{d t})$ .
According to Newton.s second law of motion, force F = M(acceleration) $= M \frac{d v}{d t},$
$- (λ 2 π a) (\frac{a}{2} \frac{d B}{d t}) = M . \frac{d}{d t} (R ω)$
$∴ - \frac{λ 2 π a^{2}}{2} . \frac{d B}{d t} = M R \frac{d ω}{d t} \Rightarrow d ω = - \frac{λ π a^{2}}{M R} d B$
On integrating, we get $ω = - \frac{λ π a^{2} B}{M R} < b r > or$ vec omega=-(Bpia^(2)lambda)/(MR)hatk

A line charge $λ$ per unit length is pasted uniformly on to the wire of a wheel of mass $m$ and radius $R$ . The wheel has light non-conducting spokes and is free to rotate about a vertical axis as shown in $F i g . 3.166$ . A uniform magnetic field extends over a radial rigion of radius $r$ given by $B = - B_{0} ˆ k (r \leq a, a < R) = 0$ (otherwise). What is the angular velocity of the wheel this field is suddenly switched off?

A(a) $\frac{- 2 B_{0} π a^{2} r}{m R} ˆ k$
B(b) $\frac{- 2 B_{0} π a^{2} r}{3 m R} ˆ k$
C( c) $\frac{B_{0} π a^{2} λ}{m R} ˆ k$
D( d) $\frac{- B_{0} π a^{2} λ}{m R} ˆ k$
A wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

A $(M + \frac{m}{4}) R^{2}$
B $(M + m) R^{2}$
C $(M + 3 m) R^{2}$
D $(\frac{M + m}{2}) R^{2}$
A circular wheel is rotating in horizontal plane without friction about its axis. If a body is gently attached to the rim of the wheel then following is false.
AMoment of inertia increases but angular momentum remains same
Bangular velocity decreases but angular momentum remains same
CRotational kinetic energy decreases but angular momentum remains same
DAngular momentum increases but angular velocity remins same