A liquid having surface tension T and density ρ is in contact with a vertical solid wall. The liquid surface gets curved as shown in the figure. At the bottom the liquid surface is flat. The atmospheric pressure is Po.
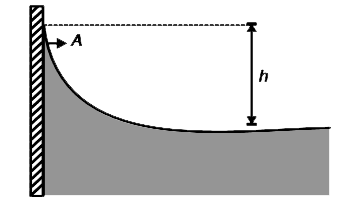
(i) Find the pressure in the liquid at the top of the meniscus (i.e. at A)
(ii) Calculate the difference in height (h) between the bottom and top of the meniscus.
The correct Answer is:(1)Po−ρgh (2) √2Tρg
Step by step video, text & image solution for A liquid having surface tension T and density rho is in contact with a vertical solid wall. The liquid surface gets curved as shown in the figure. At the bottom the liquid surface is flat. The atmospheric pressure is P_(o). (i) Find the pressure in the liquid at the top of the meniscus (i.e. at A) (ii) Calculate the difference in height (h) between the bottom and top of the meniscus. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
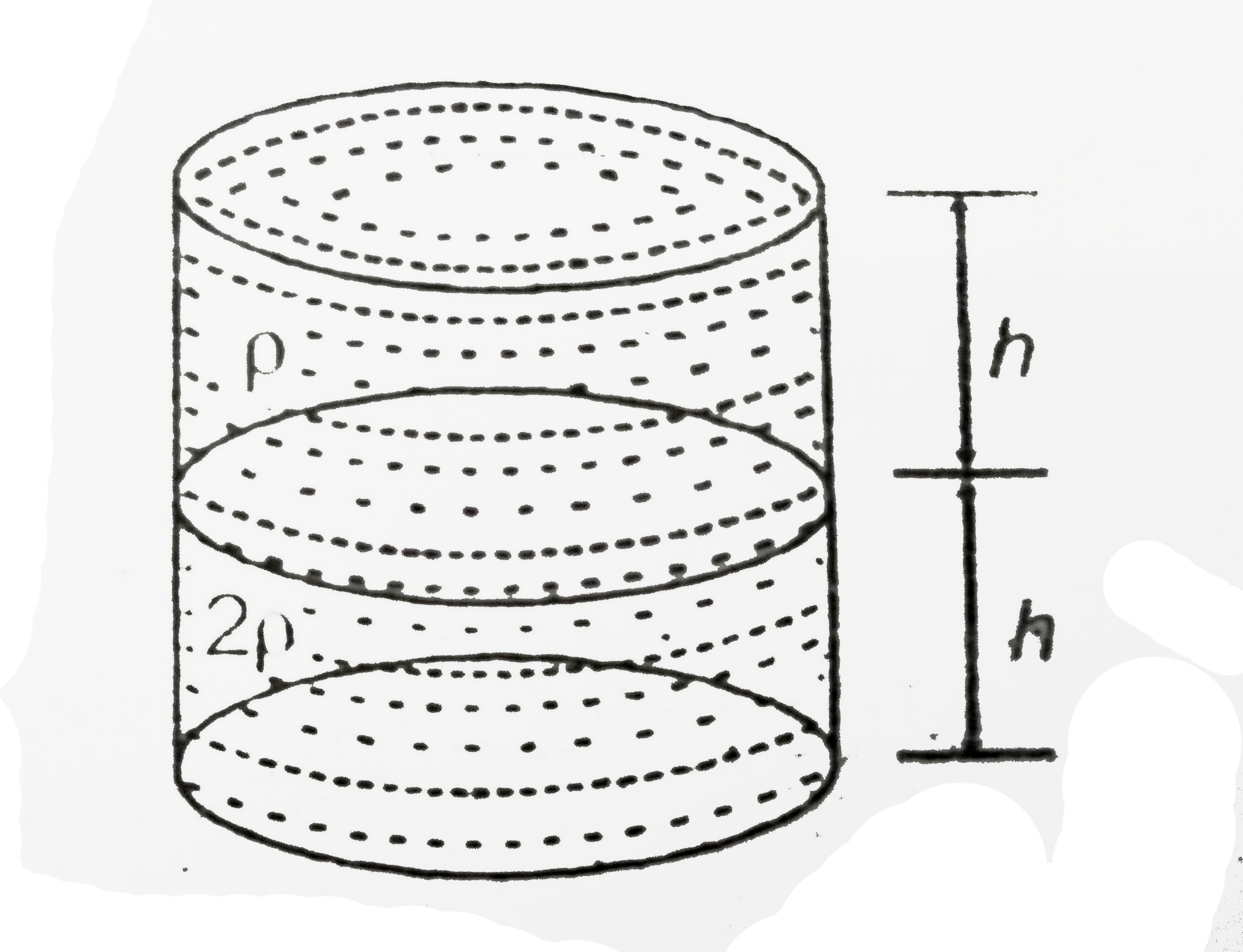
A container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View Solutiondoes angle of contact depends on the inclination of the solid surface to the liquid surface.
View Solution
Knowledge Check
Surface tension in a liquid is due to :
AAdhesive force between moleculesBCohesive force between moleculesCGravitational force between moleculesDElectrical force between molecules.A metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )
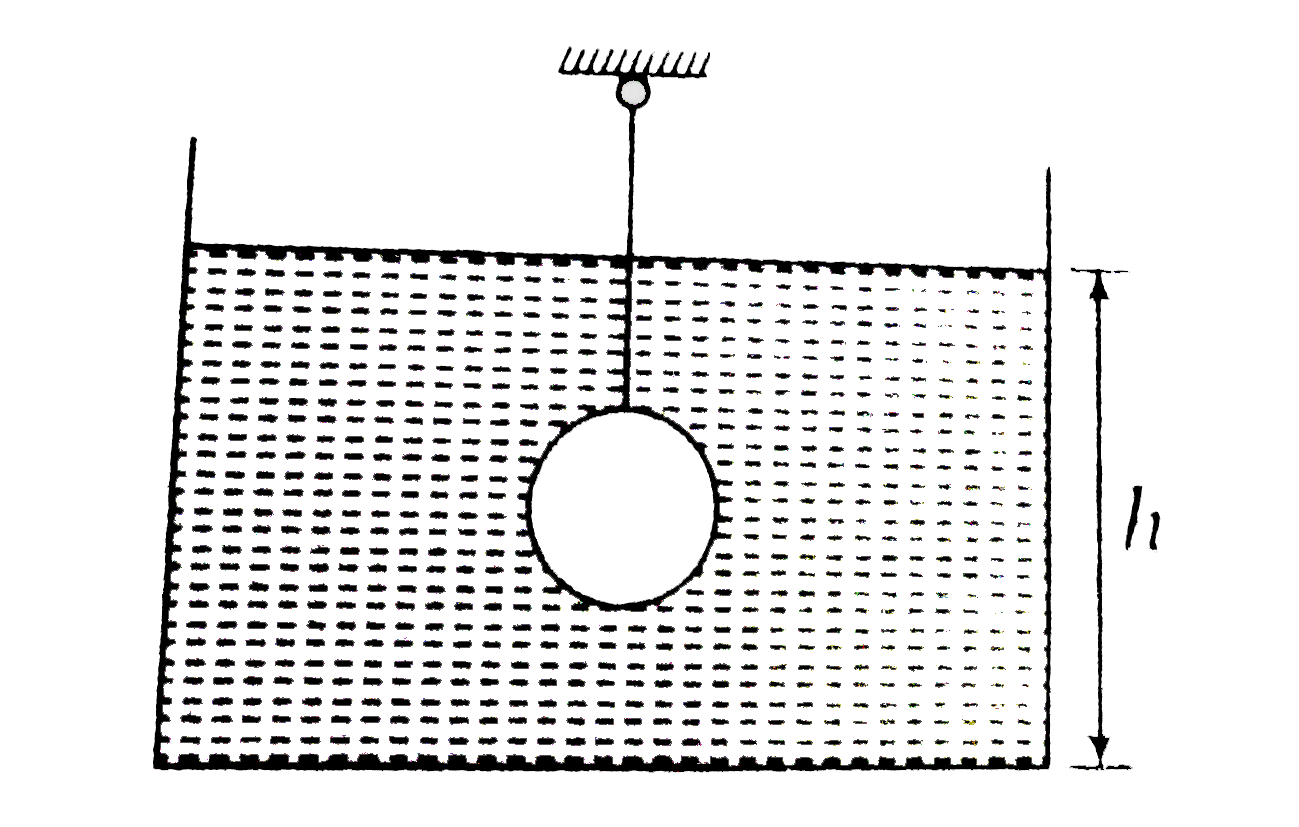 Ap=p0=ρghBp>p0+ρghCp<p0+ρghDp0
Ap=p0=ρghBp>p0+ρghCp<p0+ρghDp0If the atompspheric pressure is Pa then the jpressure P at depth a below the surface of a liquid of density ρ open to the atmosphere is
APa−ρgh2BPa−ρghCPa+ρghDP1+ρgh2
If there is no difference of pressure on the two sides of the surface, then the liquid surface is
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View SolutionA liquid will not wet the surface of a solid if the angle of contact is
View SolutionA liquid will not wet the surface of solid if the angle of contact is :
View SolutionA liquid does not wet solid surface if angle of contact is
View Solution
