A liquid of density ρ is filled in a beaker of cross section A to a height H and then a cylinder of mass M and cross-section a is made to float in it as shown in

If the atmospheric pressure is P0 find the pressure (a) at the top face B of the cylinder (b) at the bottom face C of the cylinder and (c ) at the base D of the beaker. (d) Can ever these pressure be equal ?
(a) As the top face B of cylinder is in contact with atmospherice air, so the pressure at B is atmospheric pressure i.e. PB=P0 (b) The pressure at C is due to atmospherice air and also de to weight of the cylinder, i.e., PC=P0+MgA (c ) The pressure at D is due to atmospheric air, weight of cylinder and weight of liquid in cylinder i.e., PD=P0+(Mg+HρgA)A=P0+MgA+Hρg (d) in the absence of gravity i.e., the system is in free fall (as is in satellite), then g =0 in this case PB=PC=PD=P0.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question5videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Test Your Grip A10videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - NCERT Questions73videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
A liquid of density ρ is filled in a beaker of cross section S to a height H and then a cylinder of mass m and corss section s is made to float in it as shown in figure. It the atmospheric pressure is p0, find the pressure a at the top face A of the cylinder b at the botom face C of the cylinder and c. at the base B of the beaker. Can ever these three pressures be equal?
 View Solution
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View Solution
Knowledge Check
- Question 1 - Select One
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
AhBaCρDg - Question 2 - Select One
A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as ρ=k/r2 where k is constant . The resistance of the cylinder is -
AπklA2B2πklA2CπklADNone - Question 3 - Select One
In the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (If P0 is the atmospheric pressure).
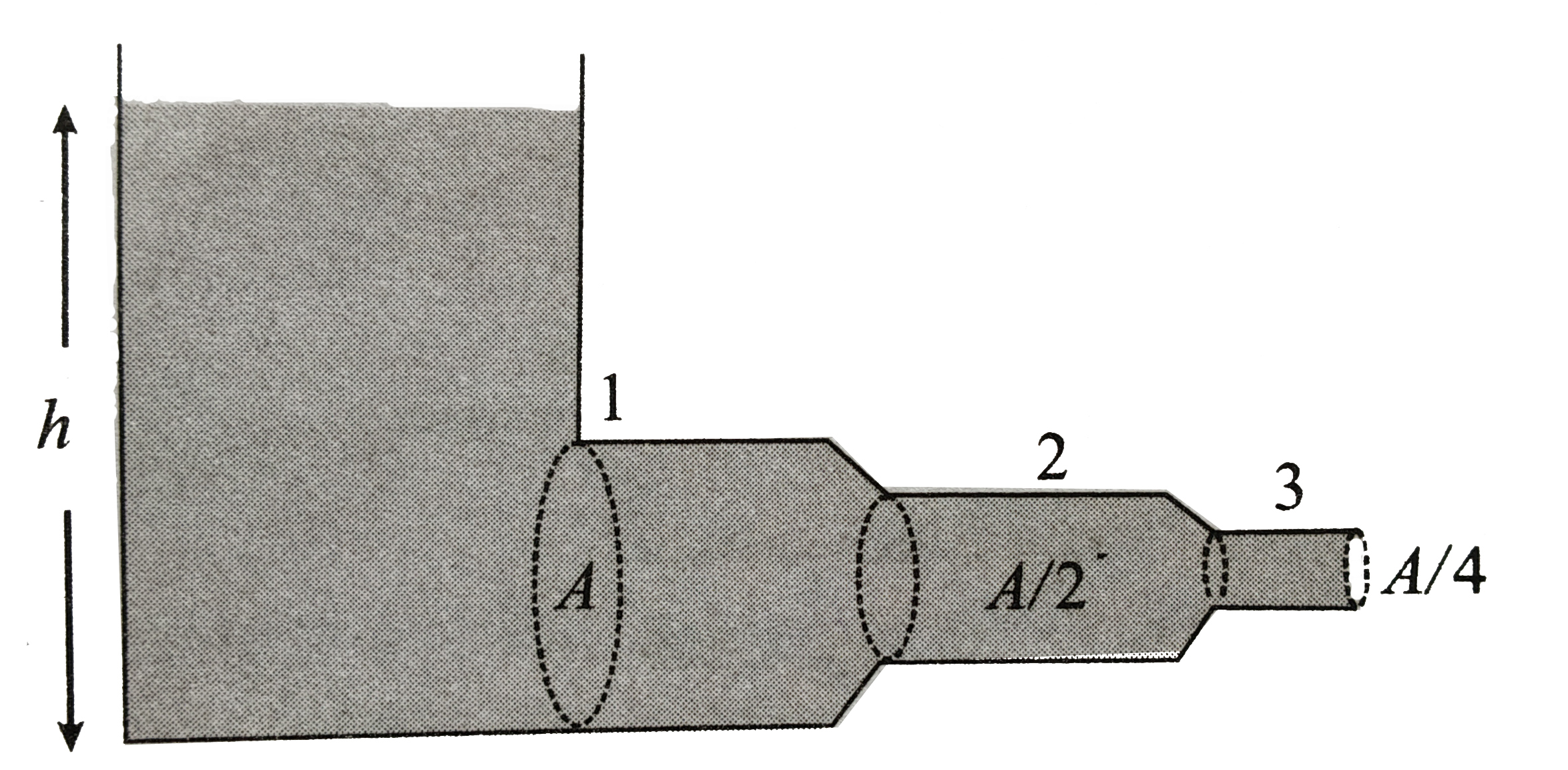 A√2hg,P0+ρhg2B√hg,P0+ρhg2C√hg2P0+3ρhg4D√hg2,P0+3ρhg4
A√2hg,P0+ρhg2B√hg,P0+ρhg2C√hg2P0+3ρhg4D√hg2,P0+3ρhg4
A cylinder contains He at 2 atmosphere pressure and hydrogen at 1.5 atmosphere pressure. What is the pressure of the mixture of gases in the cylinder ?
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,View Solution
,View SolutionIf a solid cylinder of area of cross-section A is moving with velocity V in medium of density p then power loss of cylinder is
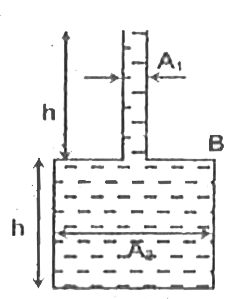
View SolutionThe vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
 View Solution
View SolutionA cylinder of certain mass is held in vertical position. If the height of the cylinder is 10 cm and radius of cross - section is 4 cm such that the pressure acting on its bottom surface is 21560N m−2 , find the mass of the cylinder ?
View Solution

