A long, circular pipe, with an outside radius R, carries a (uniformly distributed) current i0 (into the paper as shown in Fig.) A wire runs parallel to the pipe at a distance 3R from centre to centre. Calculate the magnitude and direction of the current in the wire that would cause the resultant magnetic field at point P to have the same magnitude, but the opposite direction, as the resultant field at the centre of the pipe.

Suppose wire carries current i1 and in the same direction as that
of the pipe.
Magnetic field at the centre of the pipe=−μ0i16πRˆj=μ0i16πR(−ˆj)

Megnetic field at point P
μ0i02π(2R)ˆj−μ0i12πRˆj=(μ0i04πR−μ0i12πR)ˆj
Now magnitudes are equal
μ0i16πR=μ0i04πR−μ0i12πR⇒i1=3i08
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )10videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
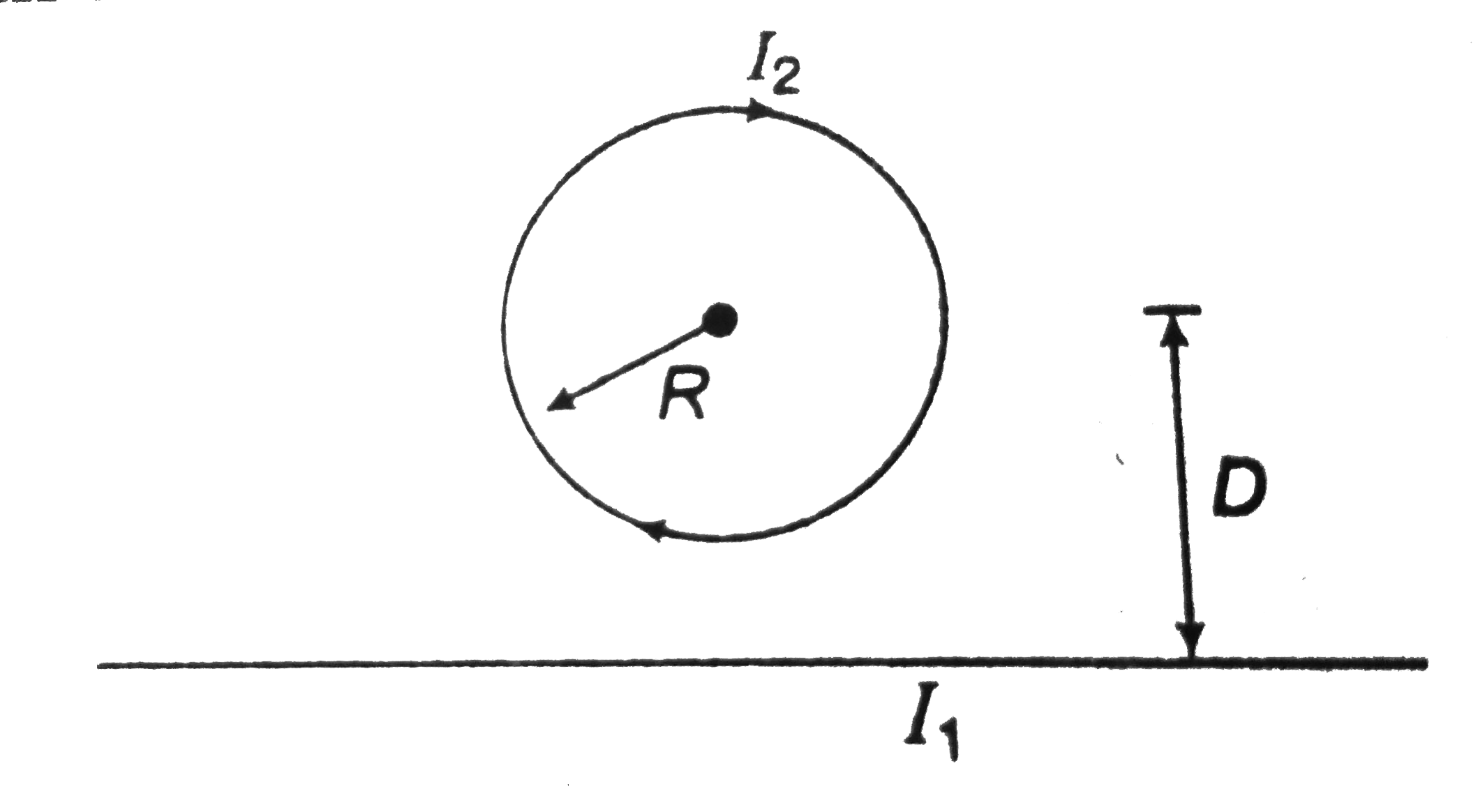
A circular loop has radius R and carries current I2 in a clockwise direction (as shown in Fig.) The centre of the loop is at a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the center of the loop is zero?
 View Solution
View SolutionA circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
Aμ0I2π(R−x)Bμ0I2πxCμ0I2π(R+x)Dnone of these - Question 2 - Select One
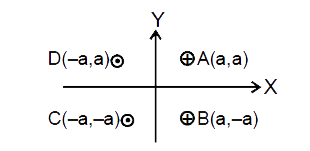
Four long wires each carrying current I as shown in Fig. are placed at points A, B, C and D. Find the magnitude and direction of

magnetic field at the centre of the square.Aμ04π(Ia) along Y-axisBμ04π(4Ia) along X-axisCμ04π(4Ia) along Y-axisDNone of these
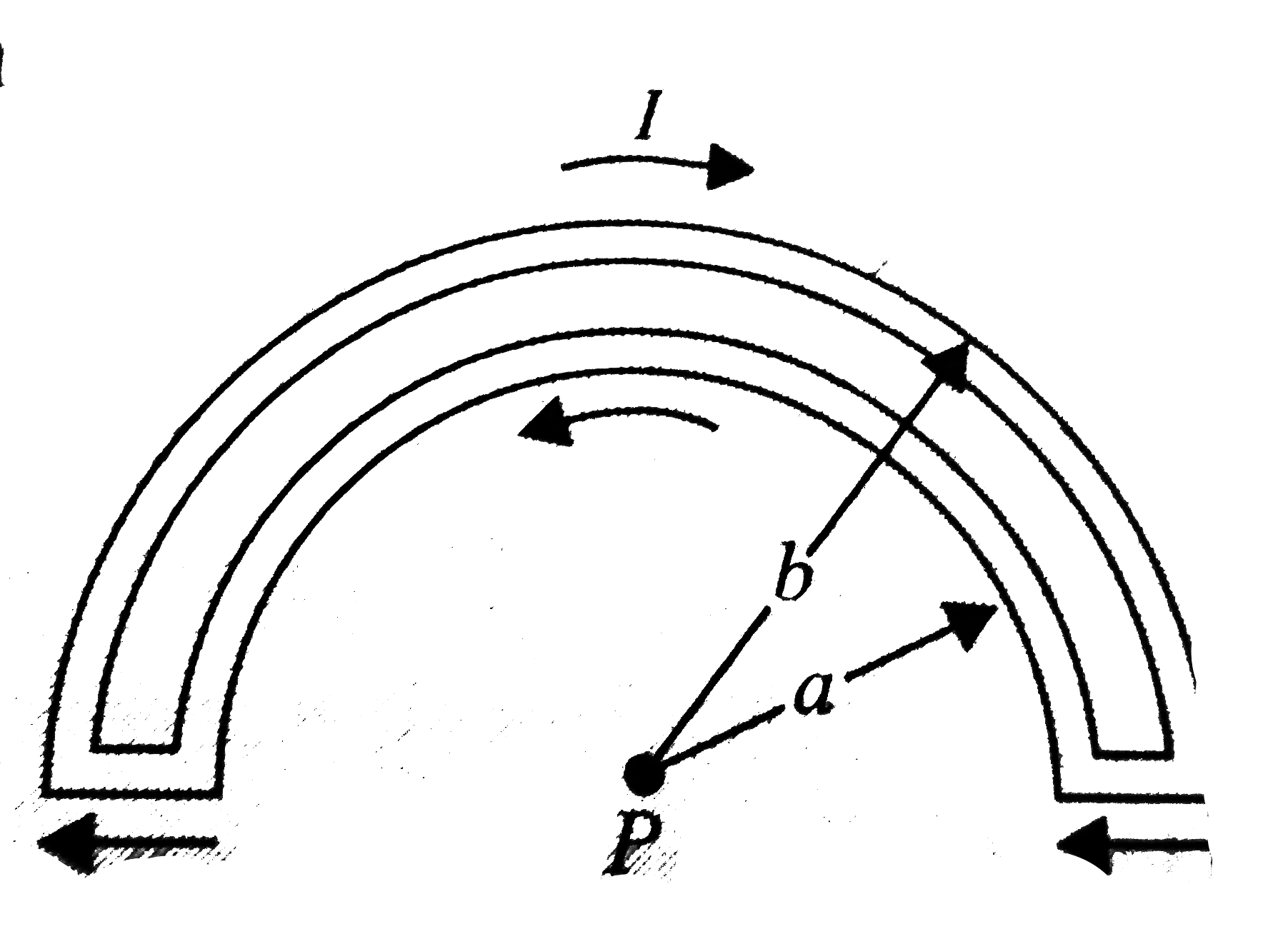
Two semicircles shown in Fig. have radii a and b. Calculate the net magnetic field (magnitude and direction) that the current in the wires produces at point P.
 View Solution
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in
 View Solution
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionFour long wires each carrying current I as shown in the figure are placed at the points A, B, C and D. Find the magnitude and direction of
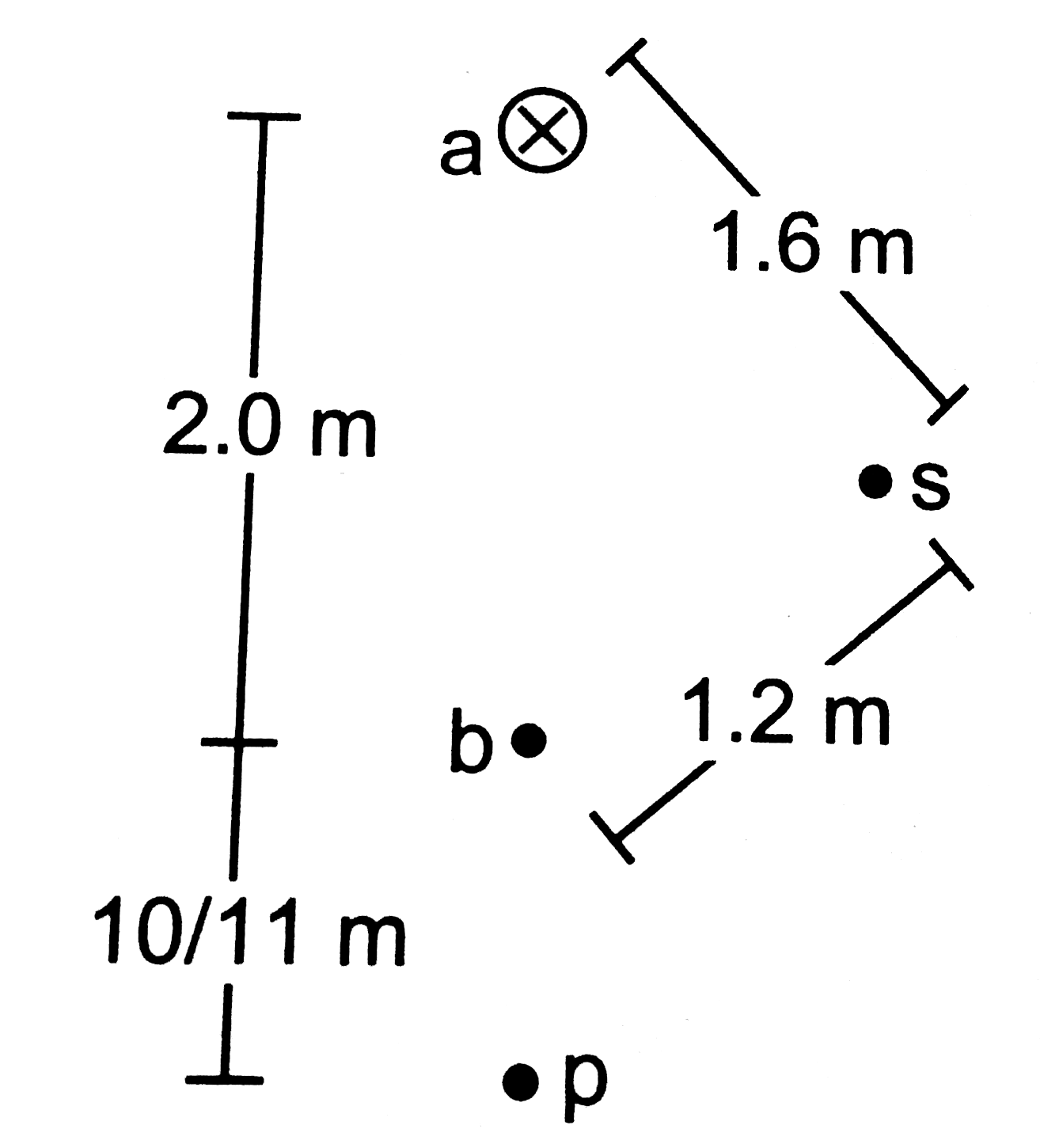
magnetic field at the centre of the square.View SolutionTwo long, straight wires a and b are 2⋅0 m apart,
perpendicular to the plane of the paper as shown in figure
. The wire a carries a current of 9⋅6A directed
into the plane of the figure,The magnetic field at the
point P at a distance of 10/11 m from the wire b is zero.
Find (a) the magnitude and direction of the current in b,
(b) the magnitude of the magnetic field B at the point s
and (c) the force per unit length on the wire b.
 View Solution
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
 View Solution
View Solution

