A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
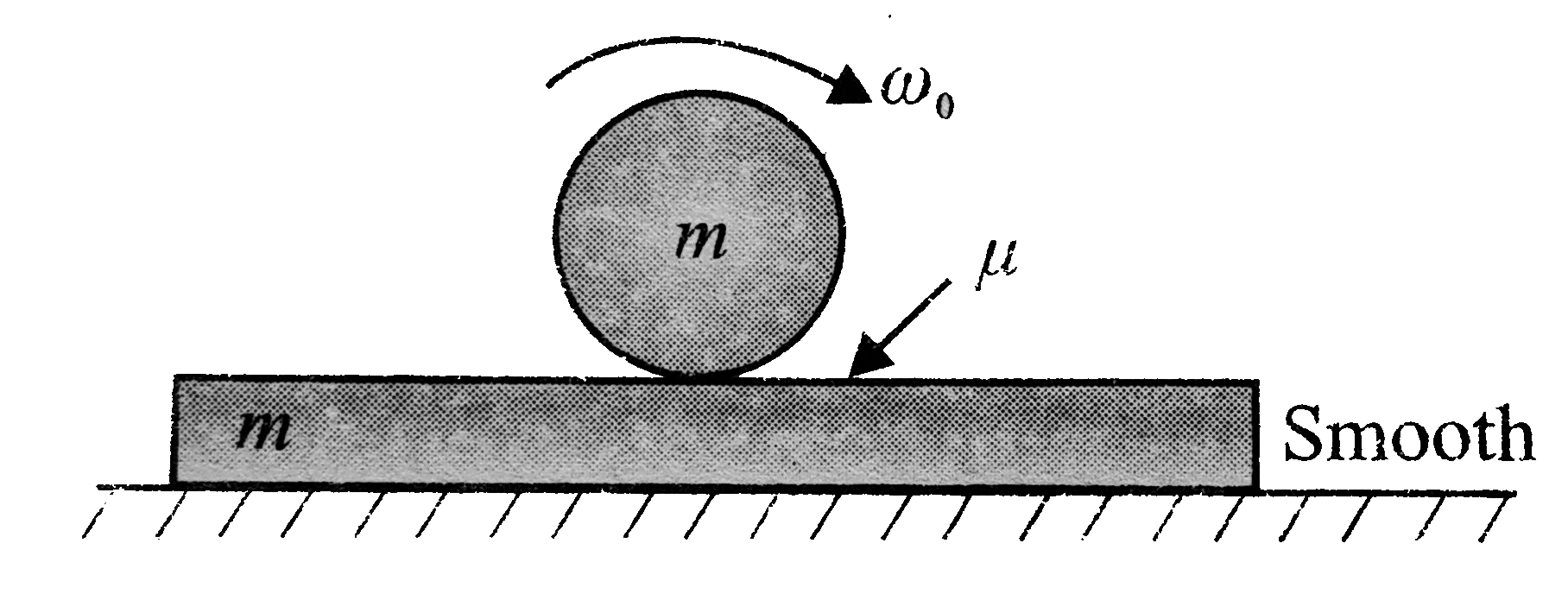
Find the time t at which the pure roiling starts
ω0r9μg
2ω0r9μg
ω0r3μg
2ω0rμg
The correct Answer is:B
a1=μmgm=μg,a2=μmgm=μg
v1=a1t=μgt,v2=a2t=μgt

τ=μmgr
ω=ω0+αt,
where α=−τI=μmgr25mr2=−52μgr
⇒ω=ω0−52μgrt
When the pure rolling starts
ω=v1+v2r
⇒ω0−52μgtr=2μgtr
⇒t=2ω0r9μg
Velocity of the sphere v2=μgt=2ω0r9
sP=12a1t2=12μg(2ω0r9μg)2=281ω20r2μg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.View Solution
A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.View SolutionA thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v0 and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is μ.

the cylinder given impluse t=0, than at what time pure rolling startsView Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling isView SolutionA plank A of mass M rests on a smooth horizontal surface over which it can move without friction A cabe B of mass m lies on the plank at one edge .The coefficient of friction between the plank and the cube is μ The size of cube is very small in comparison to the plank.

At what force F applied to the plank in the horizontal direction will be cube begin to slide towards the other end of the plank?View SolutionA long plank of mass M is initially at rest on a frictionless surface. A small block with mass m and initial speed u0 slides on top of the larger plank. The coefficient of friction between the block and plank is μ
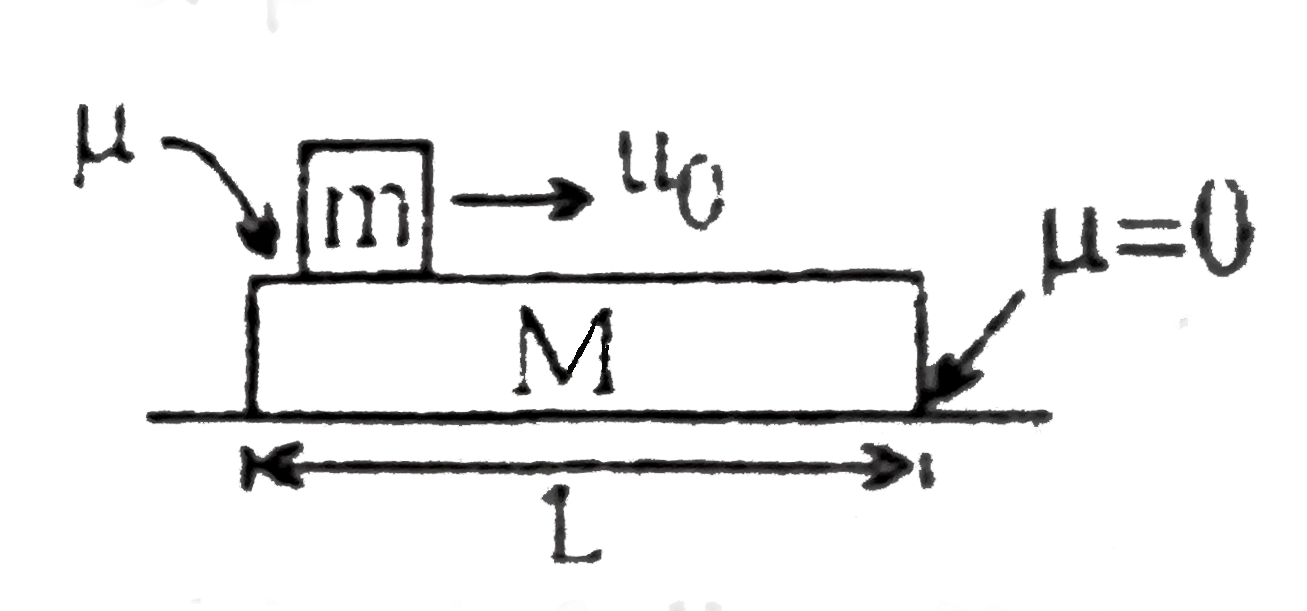
Net work done by friction if the top block falls off the plank after sliding over its length L isView SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 View Solution
View SolutionChoose the correct option:
A sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass 'm'. The co-efficient of friction between the two is μ. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of sphere relative to the plank will be
 View Solution
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
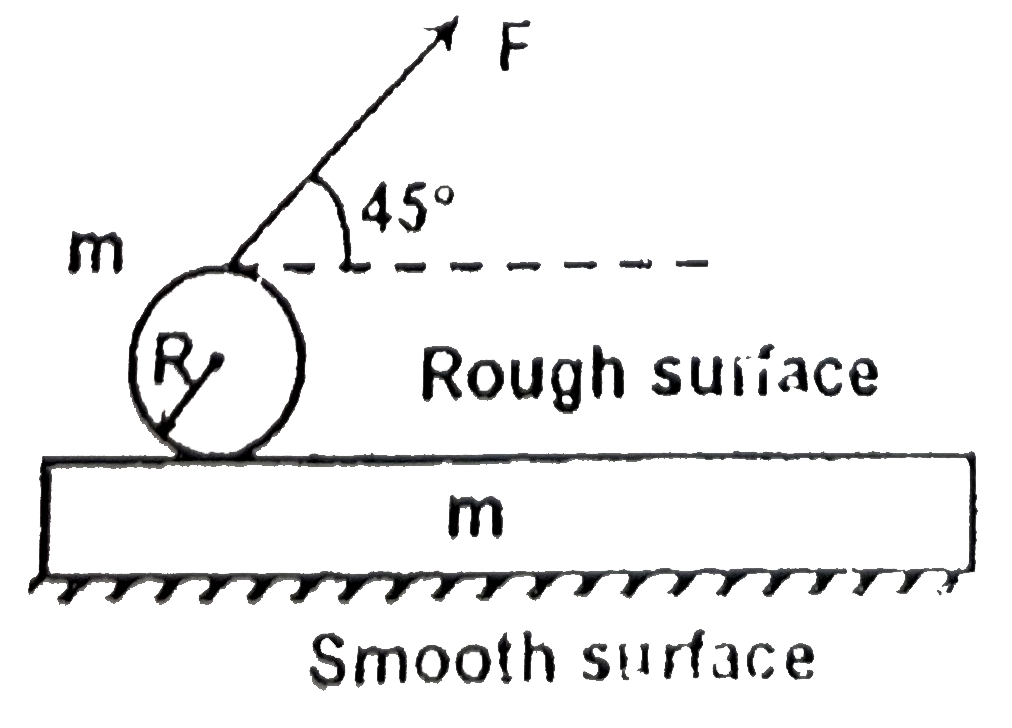 View Solution
View Solution

