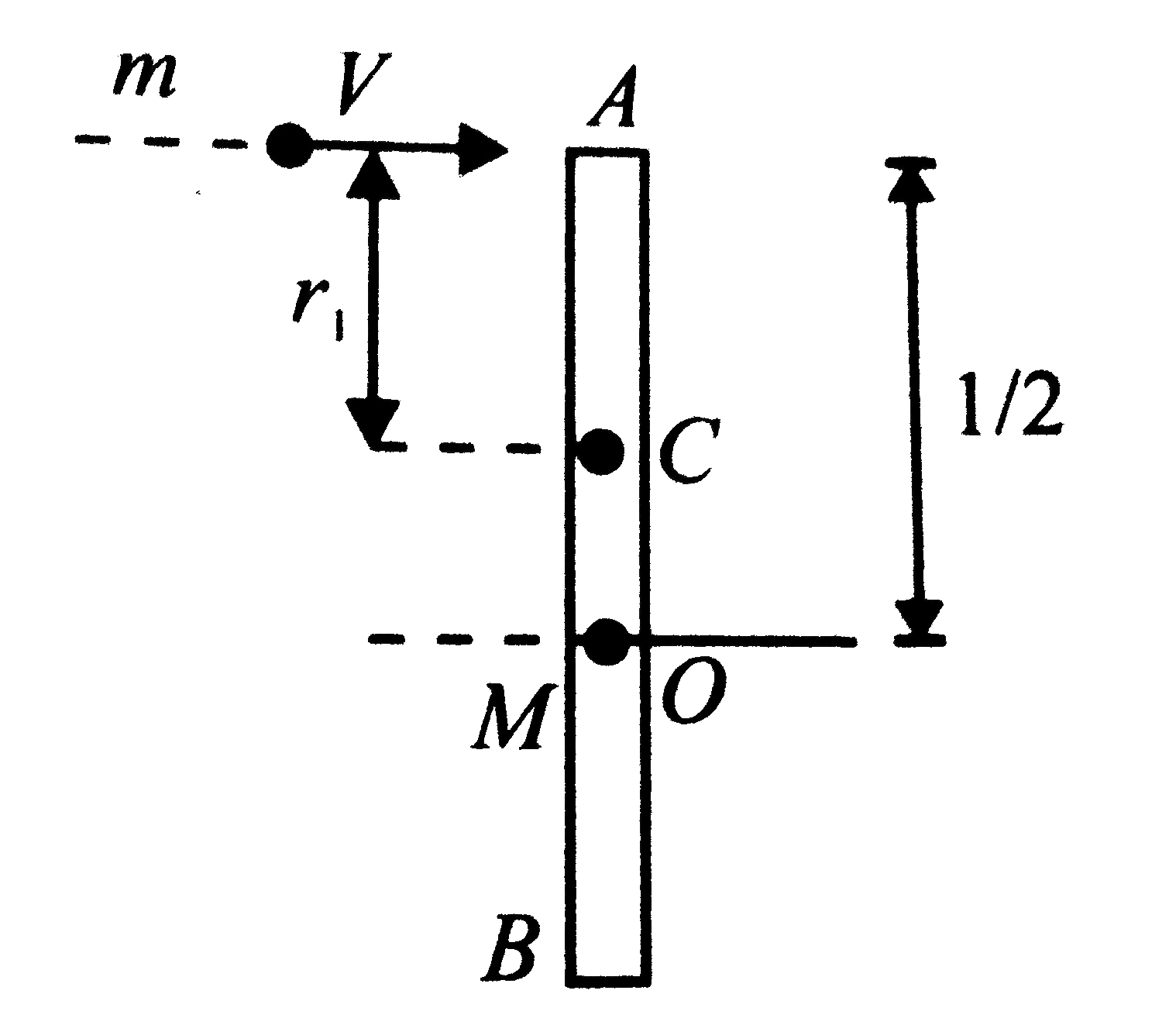
A uniform rod of mass M and length $a$ lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance $\frac{a}{4}$ from the centre and stops after the collision. Find (a). the velocity of the centre of the rod and (b). the angular velocity of the rod abut its centre just after the collision.

A

$\frac{M^{2} m v l}{4 {(M + m)}^{2}}, \frac{m^{2} M v l}{4 (m + M)}$

B

$\frac{M^{2} m v l}{2 {(M + m)}^{2}}, \frac{M^{2} M v l}{2 (m + M)}$

C

$\frac{M^{2} m v l}{{(M + m)}^{2}}, \frac{m^{2} M v l}{(m + M)}$

D

$\frac{2 M^{2} m v l}{{(M + m)}^{2}}, 2 \frac{m^{2} M v l}{(m + M)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Velocity of the centre of mass of the rod $+$ particle system
$V_{C M} = \frac{m v}{(M + m)}$

${\to v}_{p, C M} = {\to v}_{p} - {\to v}_{c}$
$v_{c} = \frac{m v}{M + m}$ and $v_{p} = v$
${\to v}_{p, C M} = \frac{M v}{M + m}$
${\to v}_{r o d, C M} = {\to v}_{r o d} - {\to v}_{C M} = 0 - \frac{m v}{M + m}$
$v_{r o d, C M} = - \frac{m v}{M + m}$
Location of the centre of mass of the system rod + particle from $A$
$r_{1} = \frac{m \times 0 + M l / 2}{(m + M)}$
$= \frac{M l}{2 (m + M)}$
Angular momentum of the particle just before collision about $C$ ,
$L_{p, c} = m v_{p, c} r_{1}$
$= \frac{M^{2} m v}{2 {(M + m)}^{2}}$
Angular momentum of the rod about the centre of mass of system $C$ ,
$L_{r o d, C M} = M v_{r o d, C M} (\frac{l}{2} - r_{1})$
$= M (\frac{m v}{M + m}) (\frac{m l}{2 (M + m)})$
$= \frac{M m^{2} v l}{2 {(M + m)}^{2}}$
Moment of inertia about the vertcal axis passing through $C$ ,
$I_{c, r o d} = I_{0} = M {(\frac{l}{2} - r_{1})}_{1}^{2}$
$I_{c, r o d} = \frac{M l^{2}}{12} + m {(\frac{m l}{2 (M + m)})}^{2}$
$I_{c, particle} = m r_{1}^{2} = m {(\frac{M l}{2 (M + m)})}^{2}$
$I_{c} = \frac{M l^{2}}{12} + M {(\frac{m l}{2 (M + m)})}^{2} + m {(\frac{M l}{2 (M + m)})}^{2}$
$I_{c} = \frac{M (M + 4 m)}{12 (M + m)} L^{2}$
As no external forces are acting on the system rod $+$ particle, hence the velocity of the centre of mass of the system will remain constant.
$v_{C M} = \frac{m v}{M + m}$
For angular velocity about $C$
$m v r_{1} = I_{c} ω$
$ω = \frac{m v r_{1}}{I_{c}} = \frac{m v (\frac{m l}{2 (M + m)})}{(\frac{M (M + 4 m) L^{2}}{12 (m + m)})}$
$= \frac{6 m v}{(M + 3 m) L}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-Linked Comprehension

Home
Ask Doubt
Profile