A long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
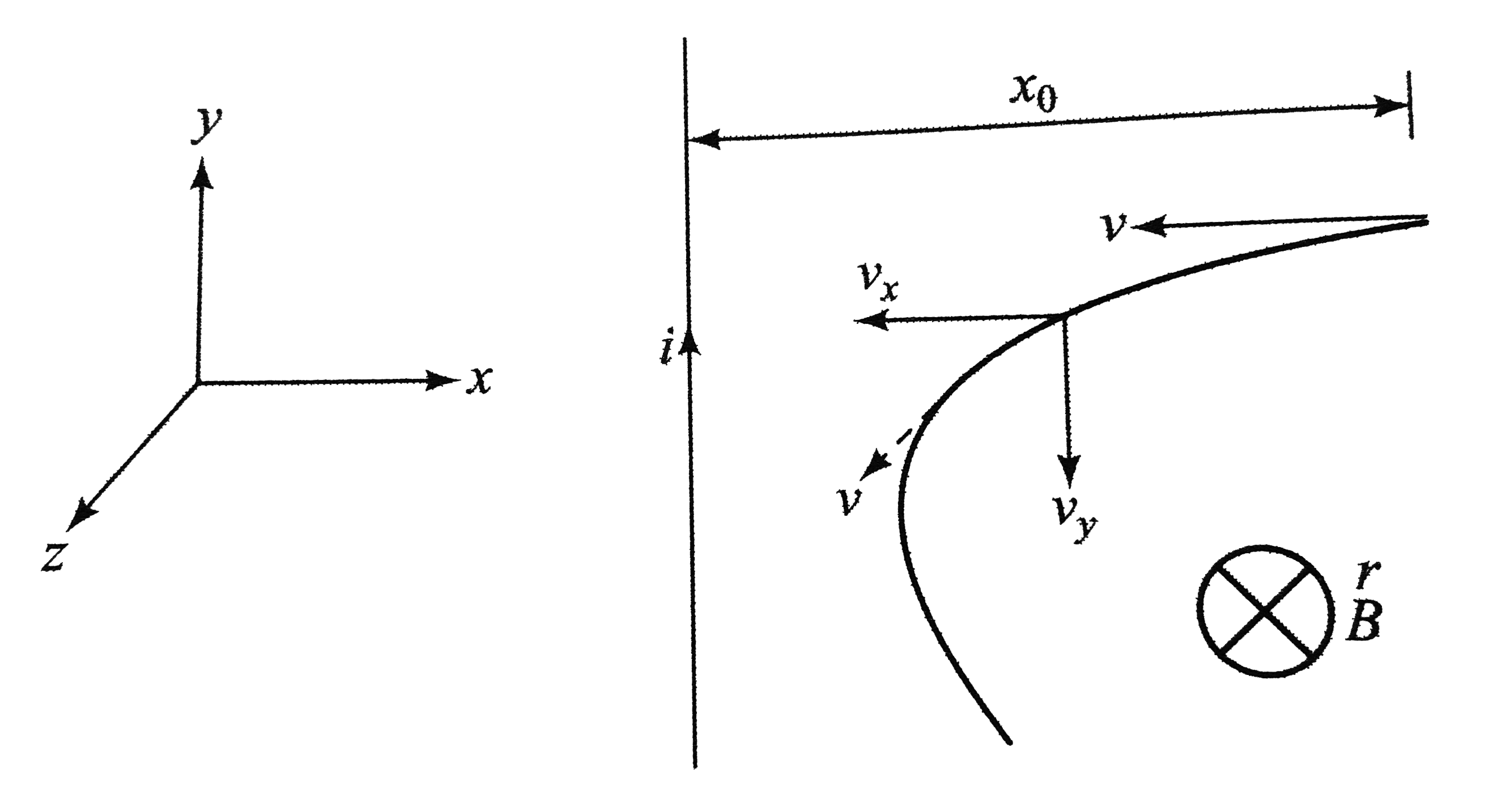
Solution: Let the particle be initially at P. Take
the wire as the y axis and the foot of perpendicular from
P to the wire as the origin. Take the line OP as the
x−aξs.Wehave,OP=x0.Themag≠ticfieldBatany<br>p∮→therightofthewireisalongthe¬ativez−aξs.<br>Themag≠ticforceonthepartic≤is,∴,∈the<br>x−ypla≠.Asthereisno∈itialvelocityalongthez−aξs,<br>themotionwillbe∈thex−ypla≠.Also,itsspeed<br>rema∈sunchan≥d.Asthemag≠ticfieldis¬<br>uniform,thepartic≤does¬goalonga∘≤.<br>Theforceattimetis( vec F)= (vec qv) xx (vec B)<br> = q((vec i)vx + (vec j)vy) xx (- (mu_0)i/2 pi x) vec k)<br> = ((vec j) q(v_x)) ((mu_0)i/2pi x) - (( vec i ) (qv_y)((mu_0)i/2 pi x)<br>Thusax=(Fxm)=−((μ0)qi2πm)(vyx)=−λ(Vyx).......(i)
whereλ=((μ0)qi2πm).
Also,ax=(dvxdt)=(dvxdx)(dxdt)=((vx)dvxdx)..........(ii)
As((vx)2)+((vy)2)=v2,
(2vx)(dvx)+((2vy)(dvy))=0
giv∈g((vx)(dvx))=−(vy)(dvy).....(iii)
From(i),(ii)and(iii),
((vy)dvydx)=λ(vy)x
or,dxx=(dvyλ).
Initiallyx=x0andvy=0.Atminiμmseparationom
thewire,vx=0sotˆvy=−v.
Thus(∫xx0)(dxx)=((∫0)−v)(dvyλ)
or,In(xx0)=(−vλ)
or, x = (x_0) (e^(-v/lambda))= (x_0) (e ^(- 2pi m v /((mu_0)qi))
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Short Answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
A long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionA long straight wire carries a current I0=100amp , a particle having a positive charge q=100C and mass m=10gms is kept at a distance x0=10m from the axis of the wire is projected away from it with a speed v0=10m/sec. Find the maximum separation between particle and wire is found to be y×10m Find y.
View Solution
Knowledge Check
A field due to a long straight wire carrying a current I is proportional to
AlBl2Cl3D√lA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
A√qλlnrπm∈0B√qλln2πm∈0C√qλln22πm∈0D√qλln2πm∈0A very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity →V, as shown, the force on the charge is
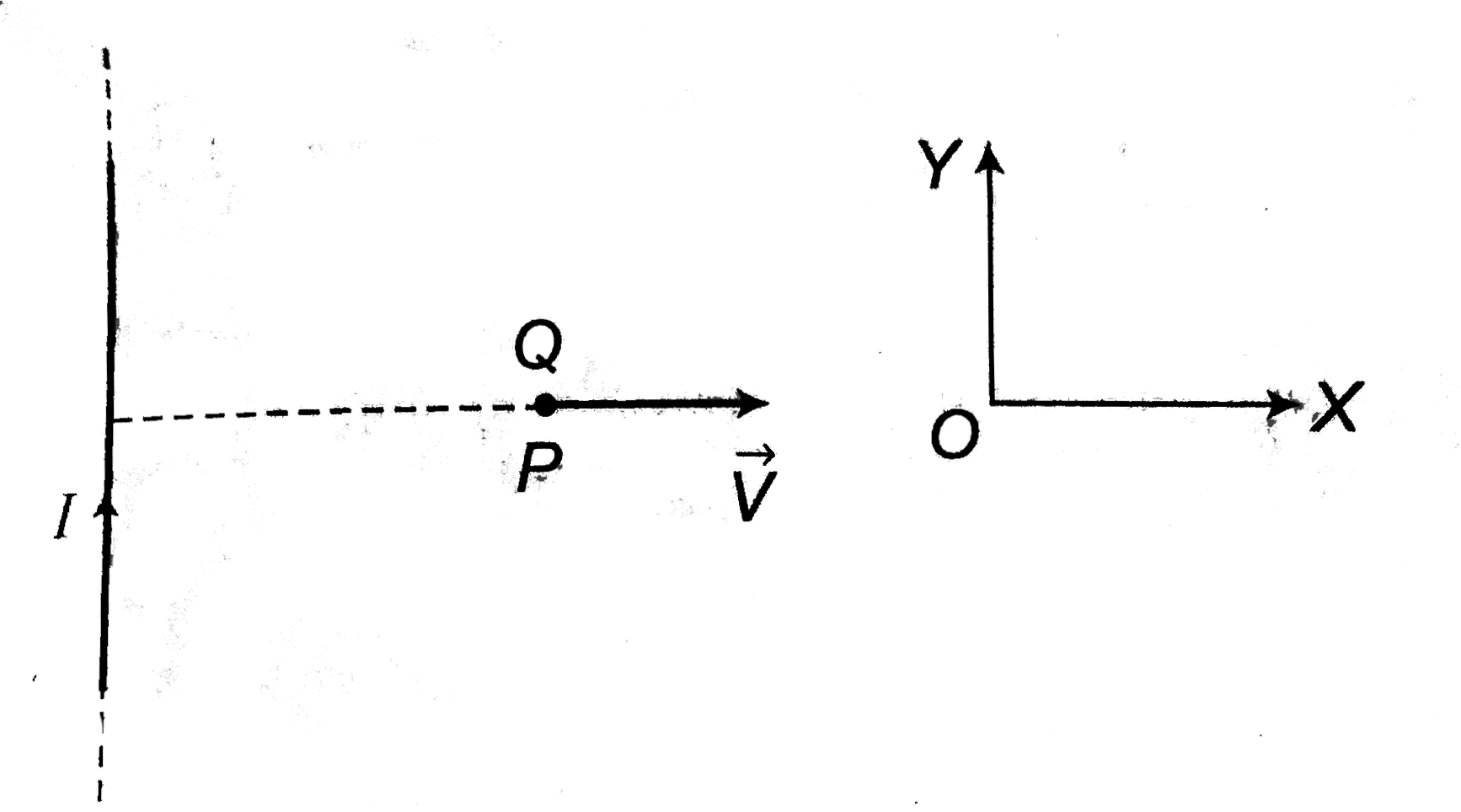 AOpposite to OXBAlong OXCOpposite to OYDAlong OY
AOpposite to OXBAlong OXCOpposite to OYDAlong OY
A positive point charge q of mass m, kept at a distance x0(in the same plane) from a fixed very long straight current is projected normally away from it with speed v.Find the maximum separation between the wire and the particle.
View SolutionConsider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
View SolutionA long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View SolutionA long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View SolutionA long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View Solution
