Consider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
Solution: As the magnetic field is uniform and the
particle is projected in a direction perpendicular to the
field, it will describe a circular path. The particle will
not hit the metal sheet if the radius of this circle is
smaller than d. For the maximum velocity, the radius
is just equal to d. Thus,
qvB=mv2d
or,qv((μ0)K2)=mv2d
or,v=((μ0)qKd2m).
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Short Answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
A long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
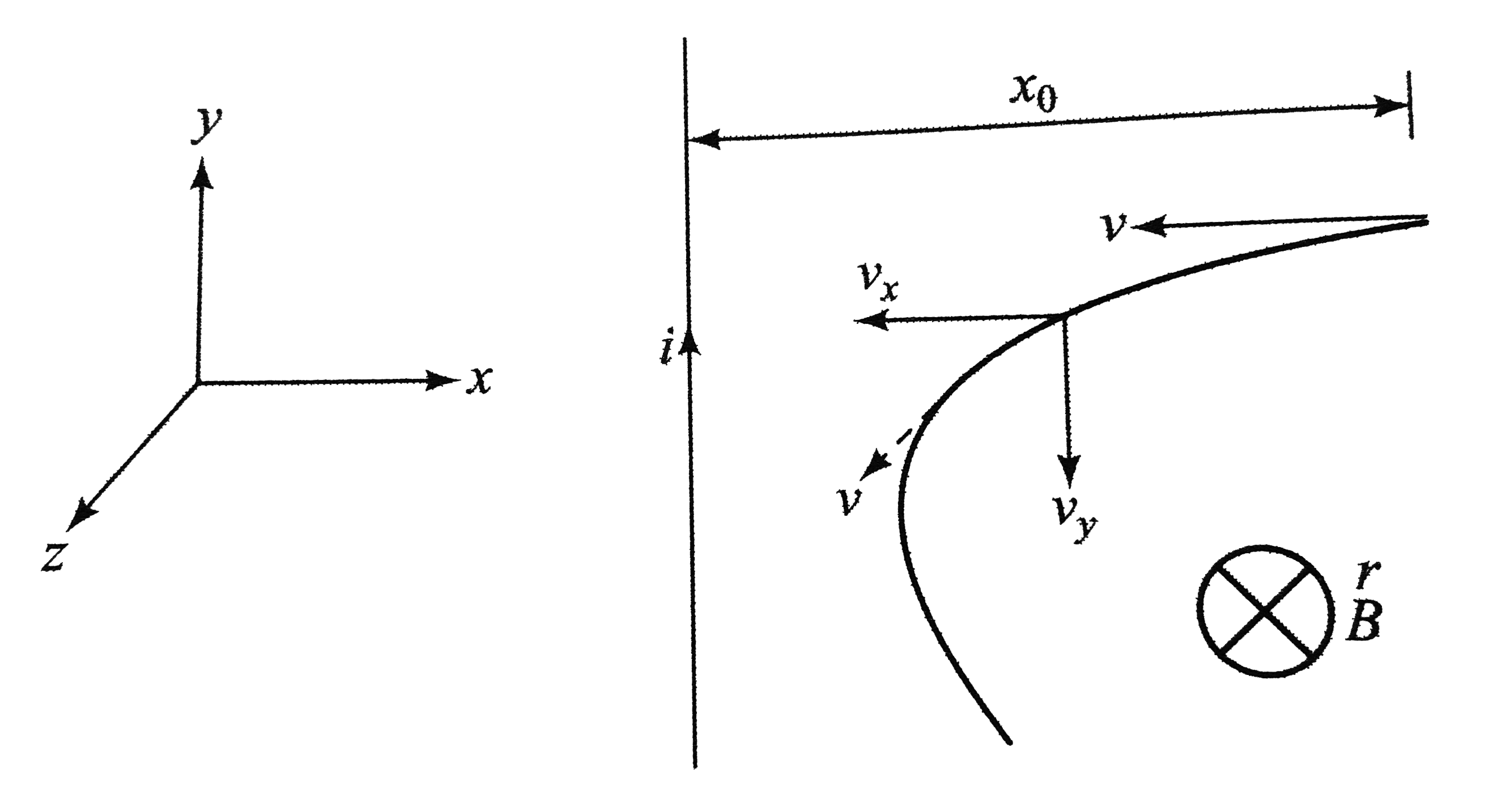

View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
View Solution
Knowledge Check
A plane metallic sheet is placed with its face parallel to lines of magnetic induction B of a uniform field. A particle of mass m and charge q is projected with a velocity v from a distance d from the plane normal to the lines of induction. Then, the maximum velocity of projection for which the particle does not hit the plate is
A2BqdmBBqdmCBqd2mDBqddA uniform magnetic field B=B0ˆj exists in space. A particle of mass m and charge q is projected towards X-axis with speed v from a point (a,0, 0). The maximum value of v for which the particle does not hit the Y-Z plane is
A2BqdmBBqdmCBq2dmDBqd2mA uniform magnetic field B=B0ˆj exists in space. A particle of mass m and charge q is projected towards X-axis with speed v from a point (a,0, 0). The maximum value of v for which the particle does not hit the Y-Z plane is
ABqamBBqa2mCBqamDBq2am
Consider the situation of the previous problem. A particle having charge q and mass m is projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View SolutionA uniform magnetic ficld B ы B0j exists in space. A particle of mass m and charge q is projected towards negative x -axis with speed v from the a point (d,0,0). If the maximum value of v for which the particle does not hit y−z plane is 4B0qdαm, then calculate α.
View SolutionFind the escape velocity of particle of mass m which is situated at a radial distance r (from centre of earth) above the earth's surface. M is the mass earth.
View Solution
