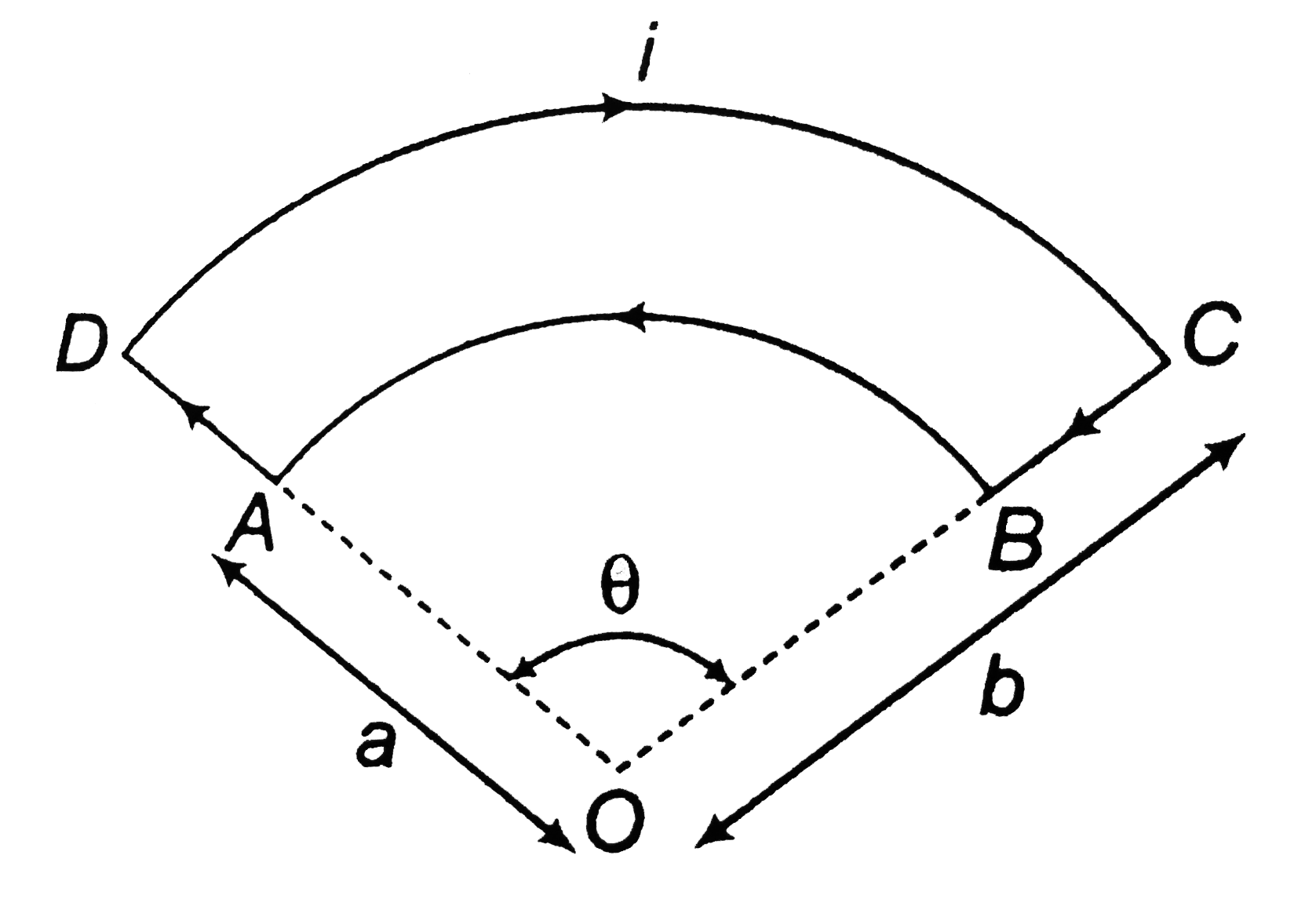
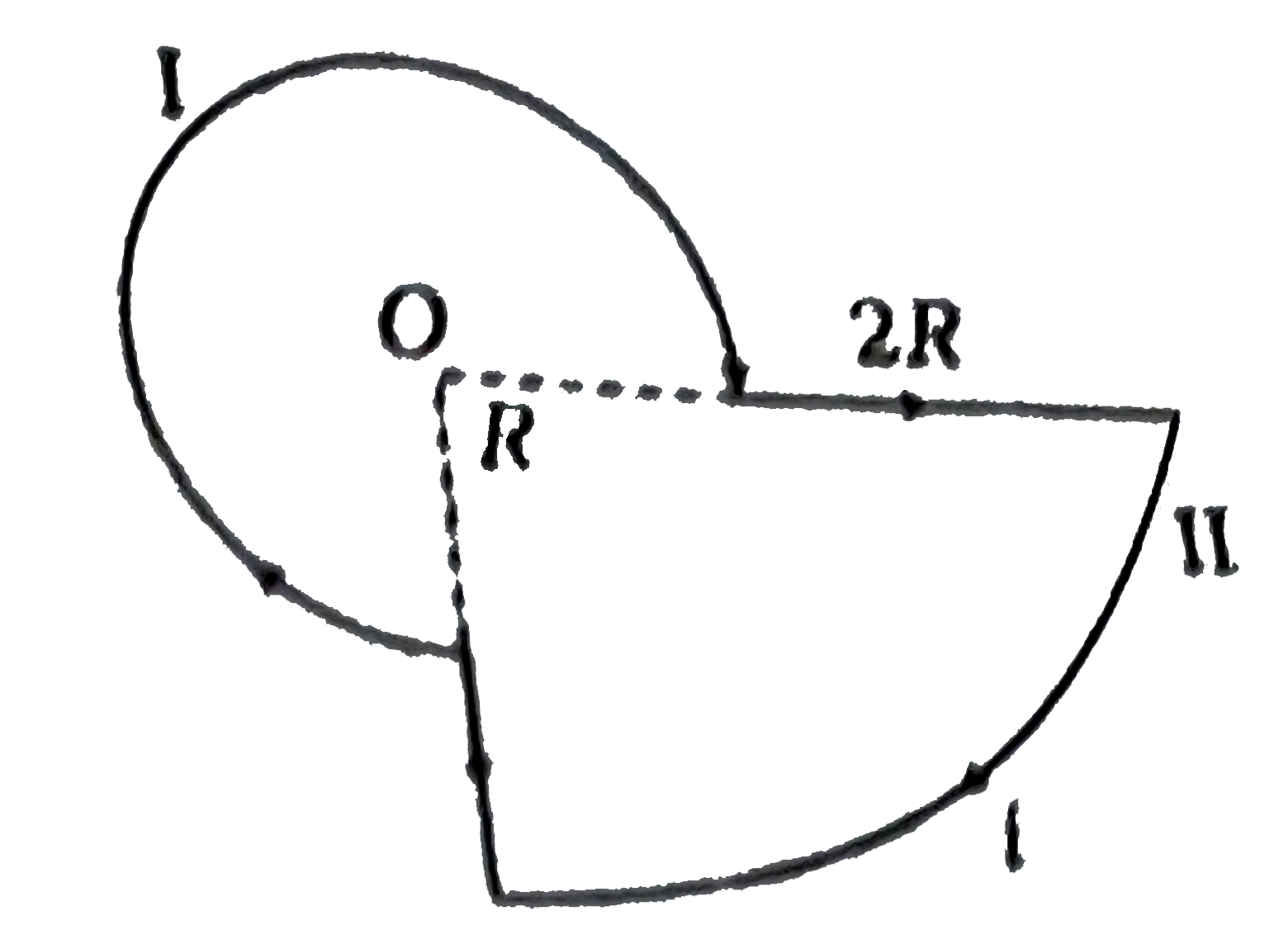
Figure shows a current loop having two circular arcs joined by two radial lines. Find the magnetic field B at the centre O.

Solution: As the point O is on the line AD, the magnetic
field at O due to AD is zero. Similarly , the field at O
due to BC is also zero. The field at the centre of a
∘a––rcurrentl∞pisgivenbyB=((μ0)i2a).Thefielddue<br>→the∘a––rarcBAwillbe<br> B_1=(theta/ 2pi)((mu_0)i/2a)<br>Theright−handthumbre–showstˆthefieldis<br>comingoutofthepla≠ofthefigure.Thefielddue→<br>the∘a––rarcDCis<br> B_2= (theta/2 pi)((mu_0)i/2b) <br> going into the plane of the figure. The resultant field at
O is
B= ((B_1)-(B_2))= ((mu_0)i theta(b-a)/4 pi ab)
coming out of the plane.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Short Answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
Figure shows a current loop having two circular arcs joined by two lines. Find the magnitude field B at the centre O.
View SolutionA current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
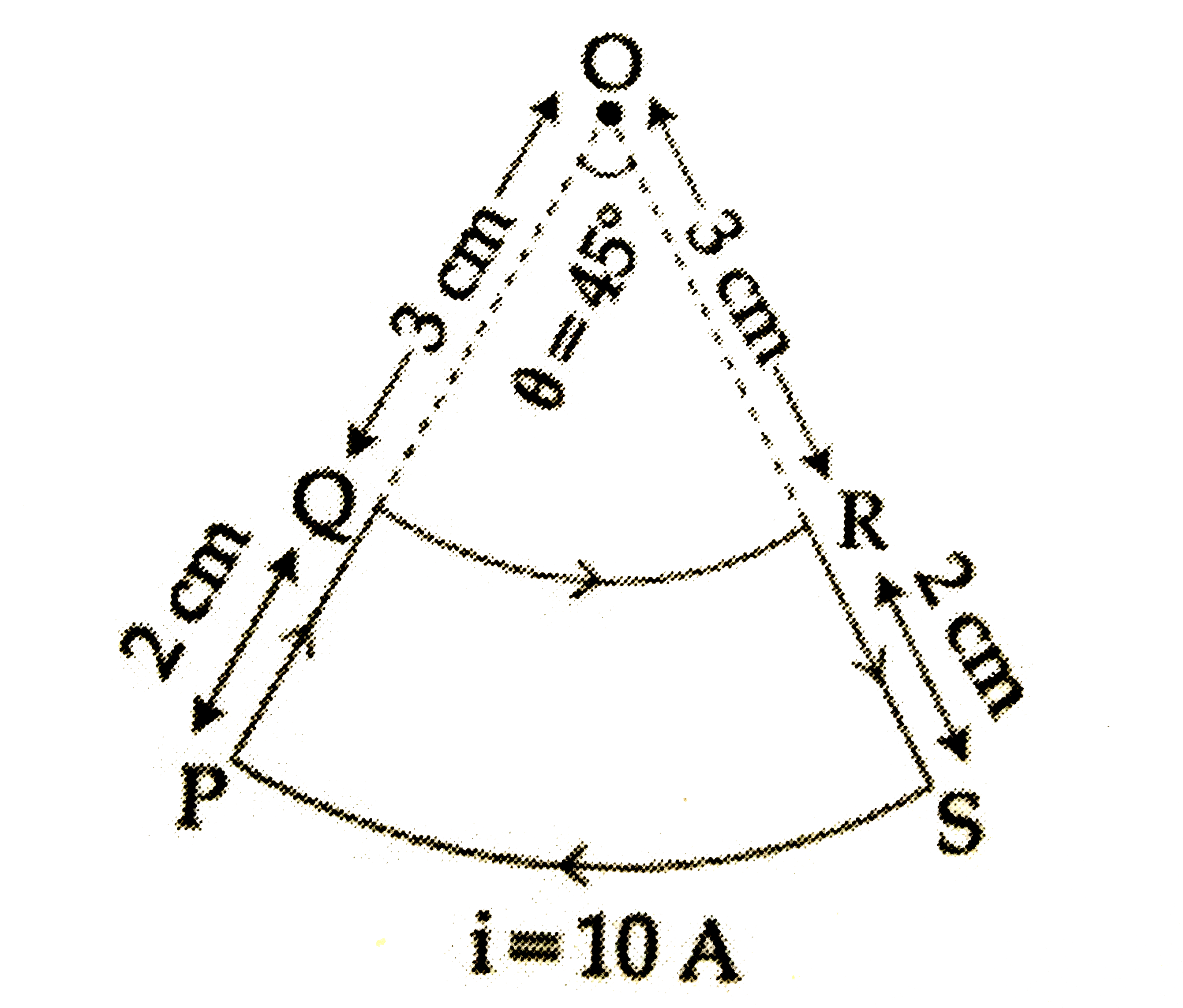
View Solution
Knowledge Check
A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
AzeroBμ04π(I1−I2)Cμ02a(I1+I2)Dμ0a(I1+I2)The magnetic field at centre O of the arc in Fig.
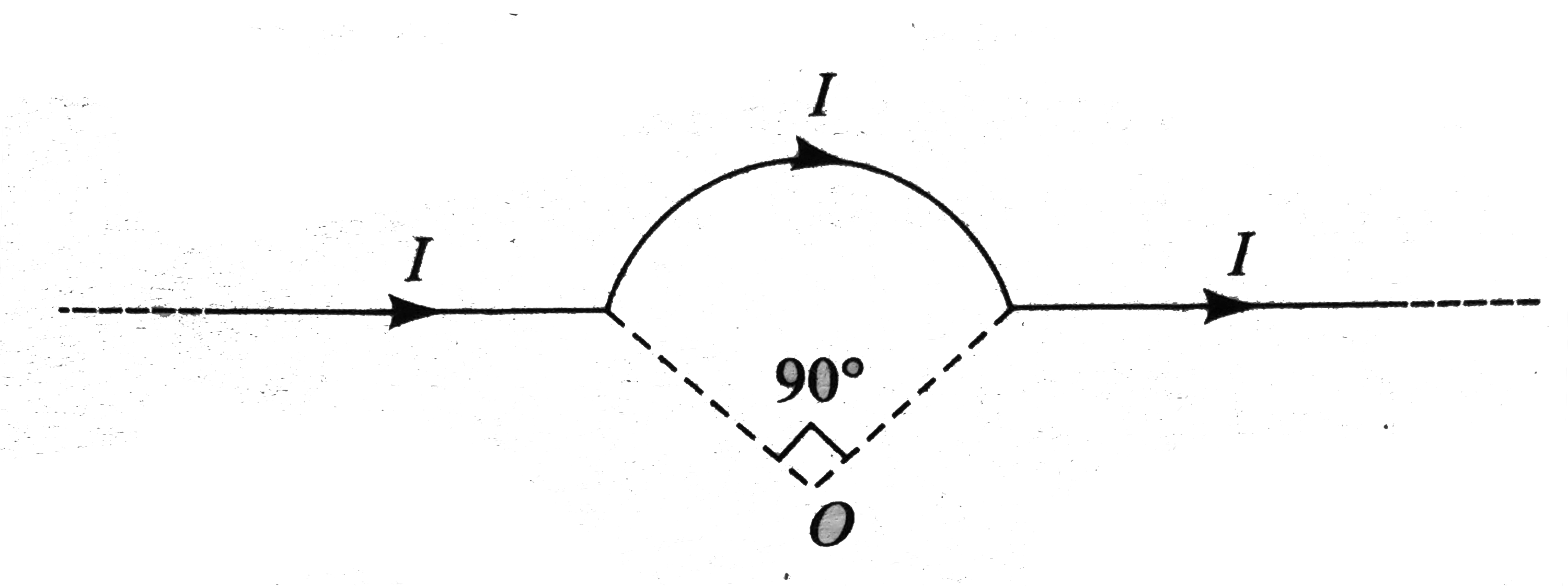 Aμ0I4π×r[√2+π]BμI2πr[π4+(√2−1)]Cμ04π×Ir[(√2−π)]DμI4π×Ir[√2+π4]
Aμ0I4π×r[√2+π]BμI2πr[π4+(√2−1)]Cμ04π×Ir[(√2−π)]DμI4π×Ir[√2+π4]In the following figure a current loop is shown which is made from two circular arcs of radii a and b(a<b), connected by radial wires. Calculate the magnetic field at the centre O.
 Aμ0iθ4πab(b−a), inwardsBμ0iθ4πab(b−a), outwardsCμ0iθ3πab(b−a), inwardsDZero
Aμ0iθ4πab(b−a), inwardsBμ0iθ4πab(b−a), outwardsCμ0iθ3πab(b−a), inwardsDZero
A current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
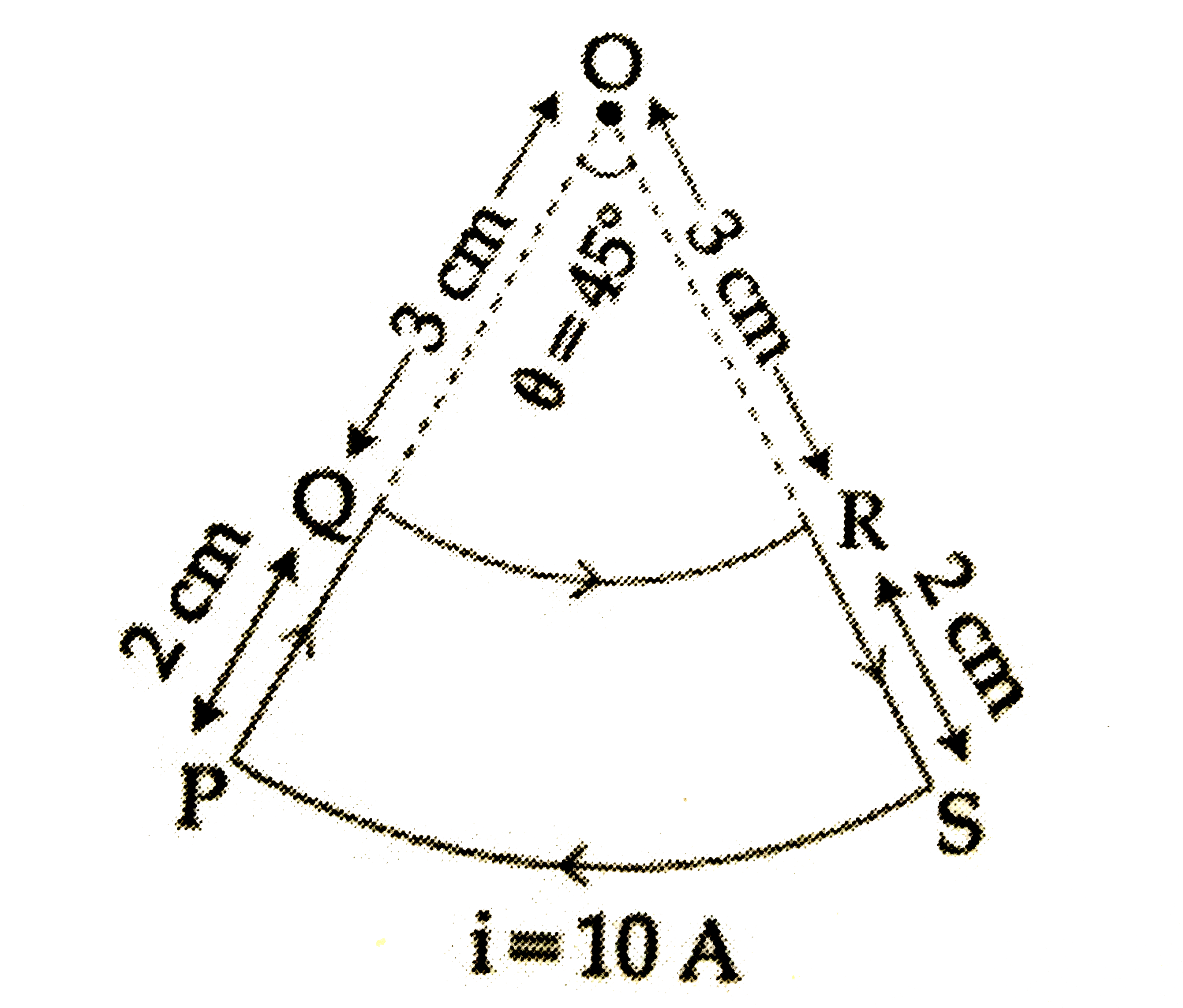
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionIn the figure-4.30 shown two circular arcs are joined to make a closed loop carrying current l. Frnd the magnetic induction at the common centre 0.

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionConsider the circular loop having current I and with central point O. the magnetic field at the central point O is
View Solution
