A magnetic field exists in the region and in the region , where is positive constant. A positive point charge moving with a velocity where is a positive constant, enters.
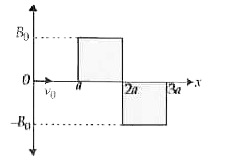
the magnetic field at x=a, The trajectory of the charge in this region can be like,
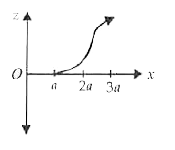
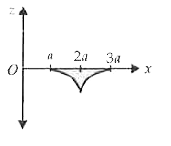
The correct Answer is:A
Force on the charge particles in a magnetic field
In the region , the force on the charge particles , must be in the direction of that is , in direction , which is vertically upward .And in the region , the force on the charged will bu in -z direction , which is vertically downwards.
For path will be concave upward.
For , path will be concave downward.
More, there should not be any kink in the path at x=2a. Hence graph (a) is correct,
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(CYCLOTRON)
2 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(FORCE ON A CURRENT CARRYING CONDUCTOR IN A UNIFORM MAGNETIC FIELD)
10 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(AMPER.S CIRCUITAL LAW AND ITS APPLICATIONS)
8 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
Similar Questions
A magnetic field →B=B0ˆj , exists in the region a<x<2a , and →B=−B0ˆj , in the region 2a<x<3a, where B0 is a positive constant . A positive point charge moving with a velocity →v=v0ˆi , where v0 is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like

View SolutionA magnetic field B=B0ˆj exists in the region a<x<2a and B=−B0ˆj, in the region 2a<x<3a, where B0 is a positive constant. A positive point charge moving with as velocity v=v0ˆi, where v0 is a positive constant, enters the magnetic field at x=a, the trajectory of the charge in this region can be like:

View Solution
Knowledge Check
A magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 A
A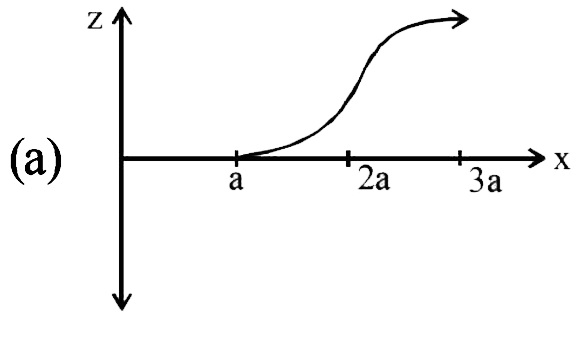 B
B C
C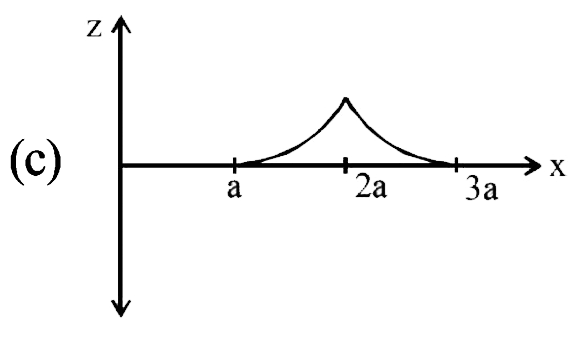 D
D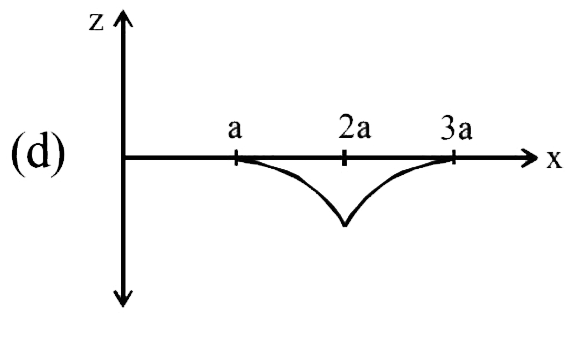
A charged particle moves with velocity →v=aˆi+dˆj in a magnetic field →B=Aˆi+Dˆj. The force acting on the particle has magnitude F. Then,
AF=0,ifaD=dA.BF=0,ifaD=−dA.CF=0,ifaA=−dD.Df∝(a2+b2)1/2×(A2+D2)1/2A portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
Aits z co-ordinate can never be negativeBits x co-ordinate can never be positiveCits x and z co-oridinate cannot be zero at the same timeDits y co-ordinate will be proportional to its time of flight
A charged particle moves with velocity →v=aˆi+dˆj in a magnetic field →B=Aˆi+Dˆj. The force acting on the particle has magnitude F. Then,
View SolutionA charged particle moves with velocity →v=aˆi+dˆj in a magnetic field →B=Aˆi+Dˆj. The force acting on the particle has magnitude F. Then,
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View Solution
