A man directly crosses a river in time t1 and swims down the current a distance equal to the width of the river I time t2. If uandv be the speed of the current and the man respectively, show that : t1:t2=√v+u:√v−u).
We know that the time taken foa a man to cross the river directly is given by t1=d√v2−u2, where d is the width of the river.
Now, if the man swims downstream then the resultant velocity is v+u. The corresponding time, t2=du+v.
Now, t1t2=v+u√v2−u2=√v+u√v+u√v+u√v−u⇒t1t2=√v+u√v−u.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
A man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
A(u+vcosθ)dvsinθB(u−vcosθ)dvsinθC(u−vcosθ)dvcosθD(u+vcosθ)dvcosθA man crosses the river perpendicular to river in time t seconds and travels an equal distance down the stream in T seconds. The ratio of man's speed in still water to the river water will be:
At2−T2t2+T2BT2−t2T2+t2Ct2+T2t2−T2DT2+t2T2−t2The ratio of downstream drift of a person in crossing a river making same angles with downstream and upstream are respectively 2 : 1. The ratio of the speed of river u and the swimming speed of person v is:
Auv=12Buv≤12Cuv≥13Duv≤3
A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
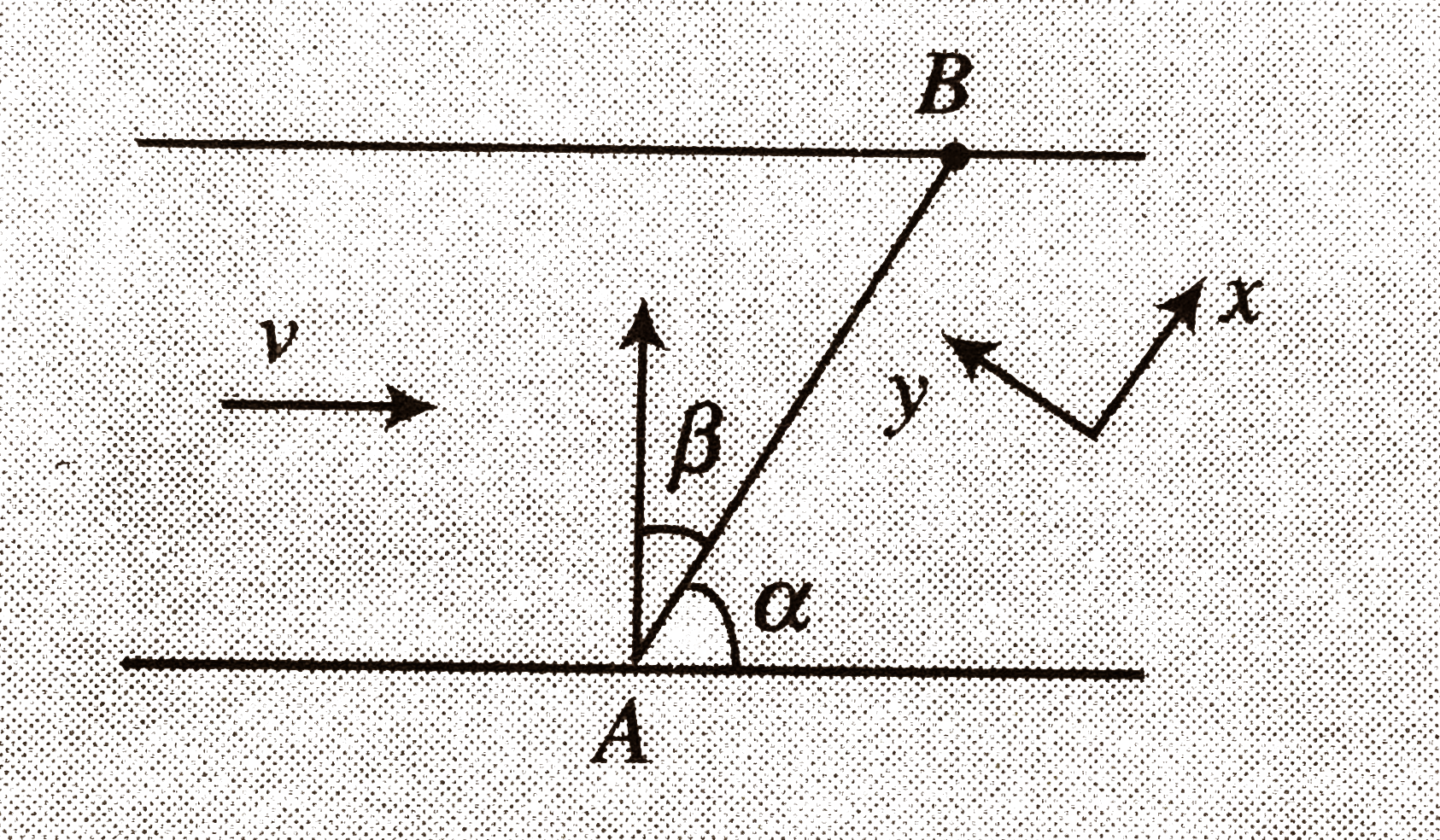 .
.
View SolutionA swimmer crosses a flowing stream of width d to and fro normal to the flow of the river at time t1. The time taken to cover the same distance up and down the stream is t2. If t3 is the time the swimmer would take to swim a distance 2d in still water, then relation between t1,t2&t3.
View SolutionVelocity of man w.r.t river is equal to velocity at river value of θ for which man reaches directly at B
View SolutionA man can swim with speed u with respect to river. The widith of river is d. The speed of the river is zero at the banks and increses linearly to V0 till mid stream of the river then decreases to zero to the other bank. When man crosses the river in shoetest time, drift is equal to: (givenu>v0)
View SolutionA man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man (for to and fro motion) is :
View Solution
