A man of mass m climbs to a rope ladder suspended below a balloon of mass M. The balloon is stationary with respect to the ground.
(a) If the man begins to climb the ladder at speed v (with respect to the ladder), in what direction and with what speed (with respect to the ground) will the balloon move?
(b) What is the state of the motion after the man stops climbing?
The correct Answer is:A, B, C, D
To solve the problem step by step, we will analyze the situation using the principles of conservation of momentum.
Step 1: Understand the System
- We have a man of mass m climbing a rope ladder attached to a balloon of mass M. Initially, both the man and the balloon are stationary with respect to the ground.
Step 2: Define the Variables
- Let v be the speed of the man climbing the ladder with respect to the ladder.
- Let VB be the speed of the balloon with respect to the ground.
- When the man climbs up, the balloon will move down due to the conservation of momentum.
Step 3: Apply Conservation of Momentum
- Since there are no external forces acting on the system (the only force acting is gravity, which does not affect horizontal motion), we can apply the conservation of momentum.
- Initially, the total momentum of the system is zero because both the man and the balloon are at rest.
Step 4: Set Up the Momentum Equation
- When the man climbs up with speed v (upward), the balloon moves downward with speed VB.
- The momentum of the man moving upward is m⋅v (upward).
- The momentum of the balloon moving downward is M⋅(−VB) (downward).
- According to conservation of momentum:
m⋅v+M⋅(−VB)=0
Rearranging gives:
m⋅v=M⋅VB
Step 5: Solve for the Speed of the Balloon
- From the equation m⋅v=M⋅VB, we can solve for VB:
VB=m⋅vM
- This indicates that the balloon moves downward with speed VB while the man climbs upward with speed v.
Step 6: Analyze the State of Motion After Climbing
- When the man stops climbing, he will no longer exert any force on the ladder.
- The system's total momentum must remain conserved. Since the man stops (his velocity becomes zero), the balloon will also come to rest.
- Thus, after the man stops climbing, the balloon will also stop moving.
Final Answers
(a) The balloon moves downward with speed VB=m⋅vM with respect to the ground.
(b) After the man stops climbing, the balloon comes to rest.
- We have a man of mass m climbing a rope ladder attached to a balloon of mass M. Initially, both the man and the balloon are stationary with respect to the ground.
- Let v be the speed of the man climbing the ladder with respect to the ladder.
- Let VB be the speed of the balloon with respect to the ground.
- When the man climbs up, the balloon will move down due to the conservation of momentum.
- Since there are no external forces acting on the system (the only force acting is gravity, which does not affect horizontal motion), we can apply the conservation of momentum.
- Initially, the total momentum of the system is zero because both the man and the balloon are at rest.
- When the man climbs up with speed v (upward), the balloon moves downward with speed VB.
- The momentum of the man moving upward is m⋅v (upward).
- The momentum of the balloon moving downward is M⋅(−VB) (downward).
- According to conservation of momentum:
m⋅v+M⋅(−VB)=0
Rearranging gives:
m⋅v=M⋅VB
- From the equation m⋅v=M⋅VB, we can solve for VB:
VB=m⋅vM
- This indicates that the balloon moves downward with speed VB while the man climbs upward with speed v.
- When the man stops climbing, he will no longer exert any force on the ladder.
- The system's total momentum must remain conserved. Since the man stops (his velocity becomes zero), the balloon will also come to rest.
- Thus, after the man stops climbing, the balloon will also stop moving.
(a) The balloon moves downward with speed VB=m⋅vM with respect to the ground.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Single Correct
Explore 23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Objective
Explore 42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A man of mass m climbs a rope of length L suspended below a balloon of mass M. The balloon is stationary with respect to ground. If the man begins to climb up the rope at a speed vrel. (relative to rope) in what direction and with what speed (relative to gound) with the balloon move ?
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m stands on a long flat car of mass M , moving with velocity V.If he now begins to run with velocity u, with respect to the car , in the same direction as V, the the velocity of the car will be
View SolutionA man of mass m moves on a plank of mass M with a constant veloicty u with respect to the plank, as shown in figure.
a.If the plank rest on smooth horizontal surface, determine the velocity of the plank.
b If the man travels a distasnce L with respect to the plank, find the distance travelled by the plank with respect to te ground.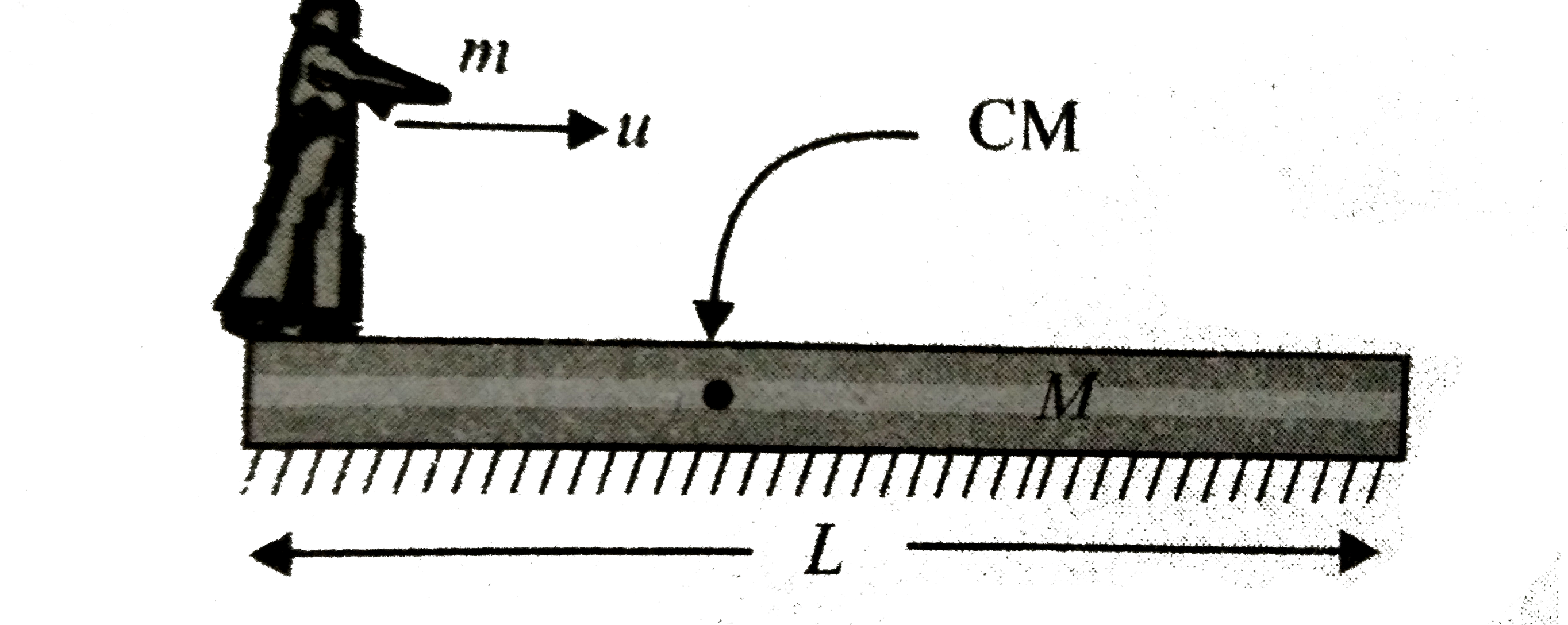
View SolutionA man of mass m starts moving on a plank of mass M with constant velocity v with respect to plank. If the plank lies on a smooth horizontal surface, then velocity of plank with respect to ground is
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA man moving with 5ms−1 observes rain falling vertically at the rate of 10ms−1. Find the speed and direction of the rain with respect to ground.
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View Solution
