A man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
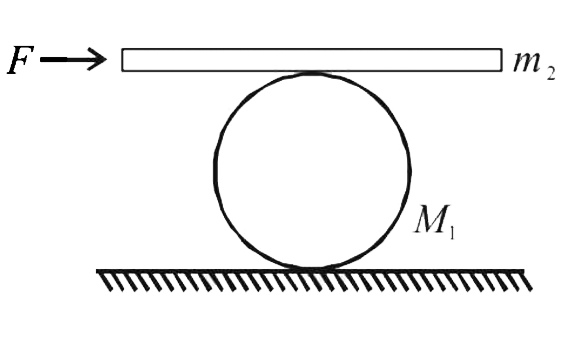
(b) the magnitudes and direction of frictional force at contact points.
Analysis of the force F in the horizontal direction on the plank as shwon in figure. Therefore the point of contact of the plank with the cylinder will try to move towards the righ. Therefore, the friction force f will act towers the left on the plank.
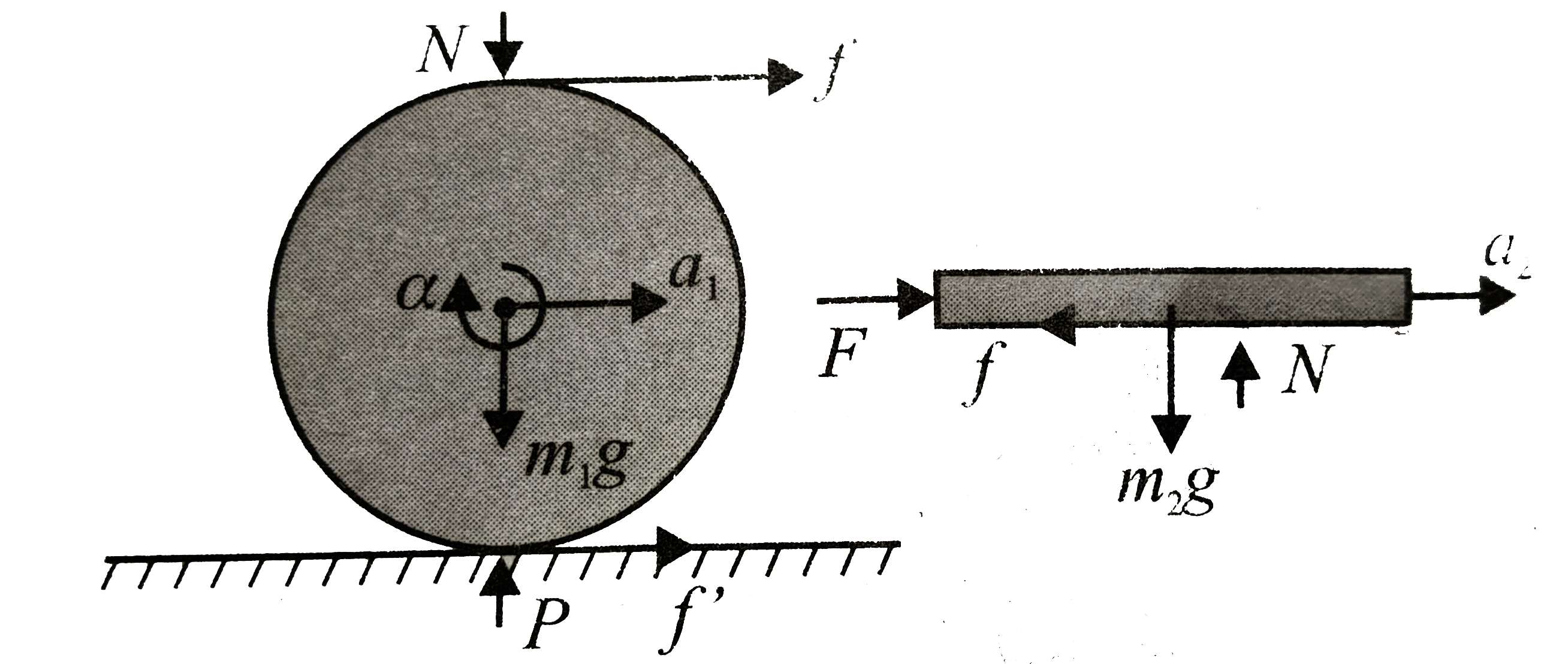
To each and every action, there is an equal and opposite reaction. Therefore, a frictional force of will act on the top of he cylinder towareds the right. Direction of f:
For finding the direction of f' first assume f' is not acting. A force f is acting on the cylinder. This force is trying to move the point of contact towards right by an acceleration aCM=fm1 acting towards the right.
At the same time, the force f is trying to rotate the cylinder about its centre of mass m the clockwise direction.
f×R=I×α⇒α=f×RI=f×R12m1R2=2fm1R
Therefore, acceleration of the point of contact
aP=aCM−αR=fm1−2fm1R×R=fm1
i.e,, towards the left.
Therefore the point of contact of the cylinder with the ground moves towards the left. therefore, fiction foce acts towards the right on the cylinder.
Here k2<Rx as k2=R22
and Rx=R.R=R2
Hence, friction should act in forward direction.
Applying Newton's law on the plank we get
F−f=m2a2.....i
Also a2=2a1....ii
Because a2 is the acceleration of the top most point of the cylinder and there is no slipping. Applying Newton's law on the cylinder.
m1a1=f+f'.........iii
The torque equation for the cylinder is
f×R−f'×R=Iα=12m1R2×(aR)
∵I=m1R2 and Rα=a1
∴1=m1R2 and Rα=a1
∴(f−f')R=12m1Ra1
∴f+f'=12m1Ra1..iv
solving eqn iii and iv we get f=34m1a1 ............v
and f'=14m1a1..........vi
From eqn i and iii F−f=2m2a1
⇒F=34m1a1=2m2a1
∴a1=4F3m1+8m2
∴a2=8F3m1+8m2
From eqn v and vi we get
f=34m1×4F3m1+8m2=3Fm13m1+8m2
and f'=14m1×a1−3Fm3m1+8m2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
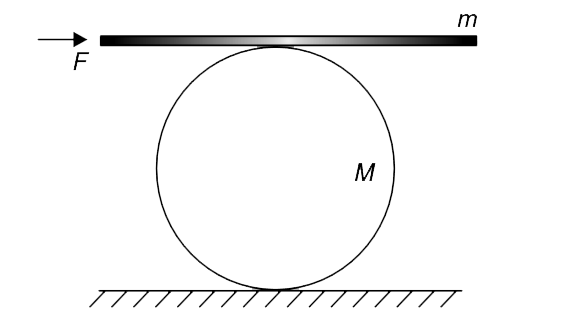
A boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
View SolutionA plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View Solution
Knowledge Check
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2mThe mass m is placed on a body of mass M. There is no friction. The force F is applied on M on it moves with acceleration a. Then, the force on the top body is
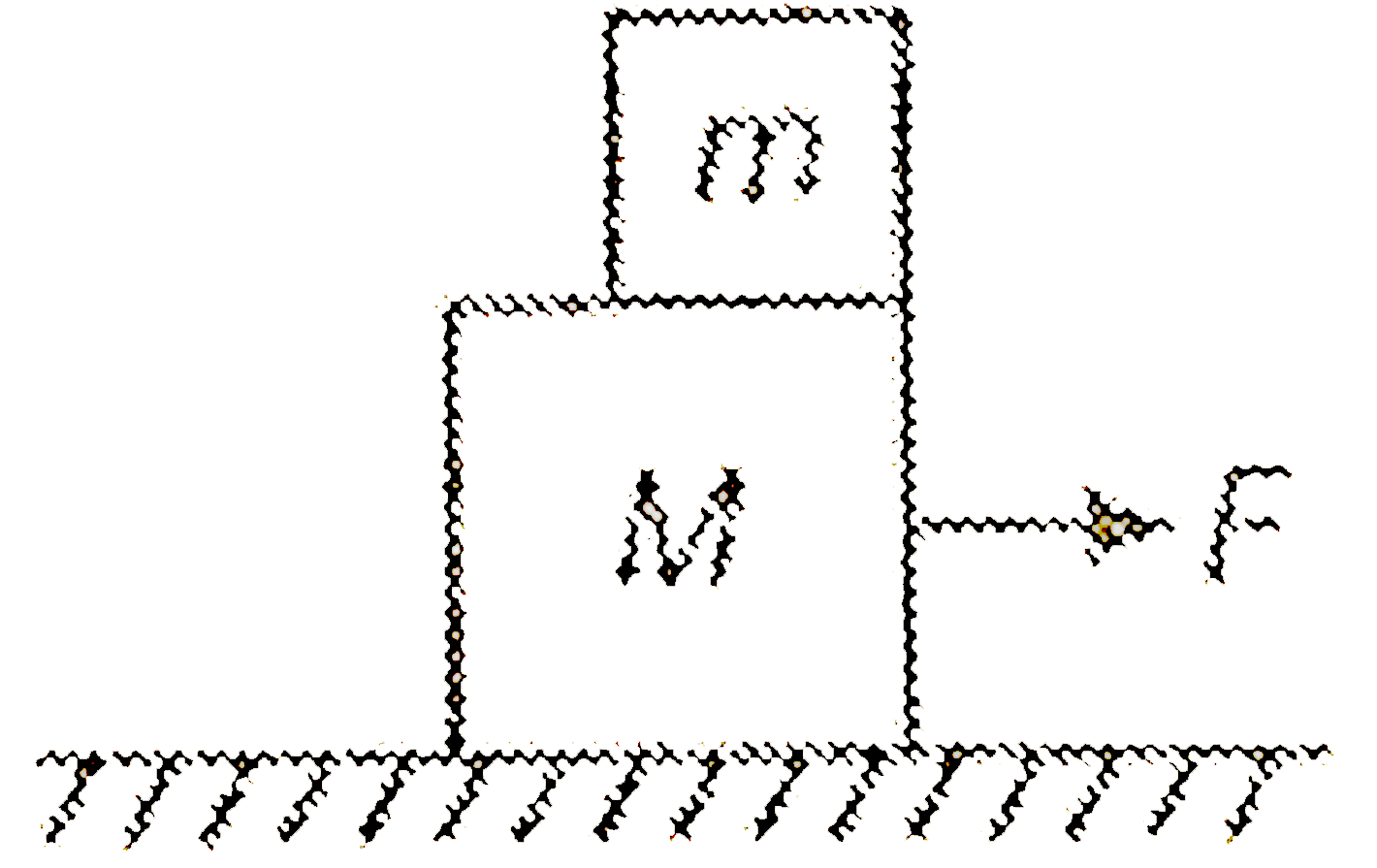 AFBmaCF - maDNone of these
AFBmaCF - maDNone of these

A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA cylinder of mass 2kg and radius 10cm is held between two planks as shown in Fig. Calculate KE of the cylinder when there is no slipping at any point.
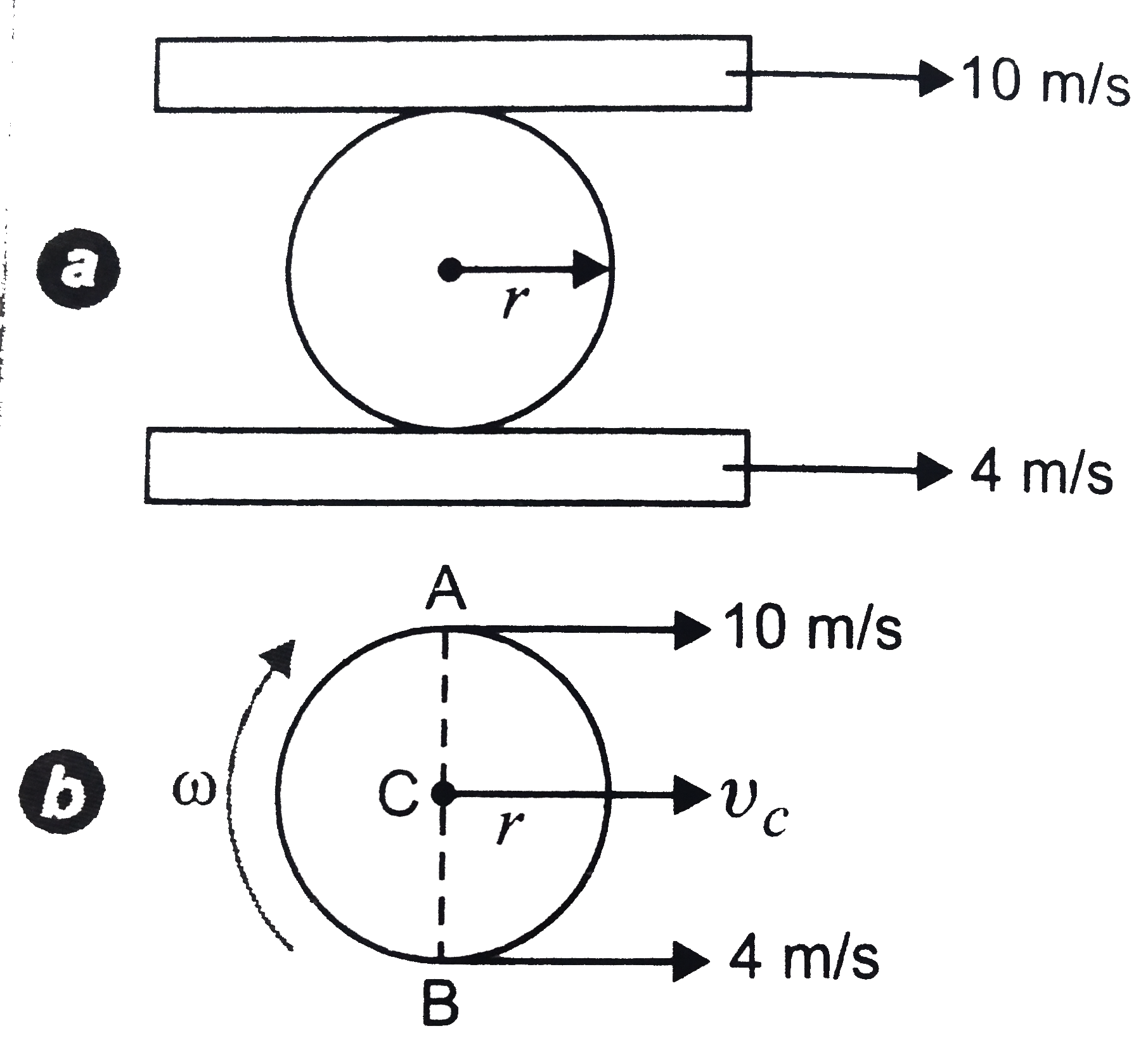
View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.
View Solution