A solid sphere of radius R is set into motion on a rough horizontal surface with a linear speed v0 in forward direction and an angular with a linear speed v0 in forward direction and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
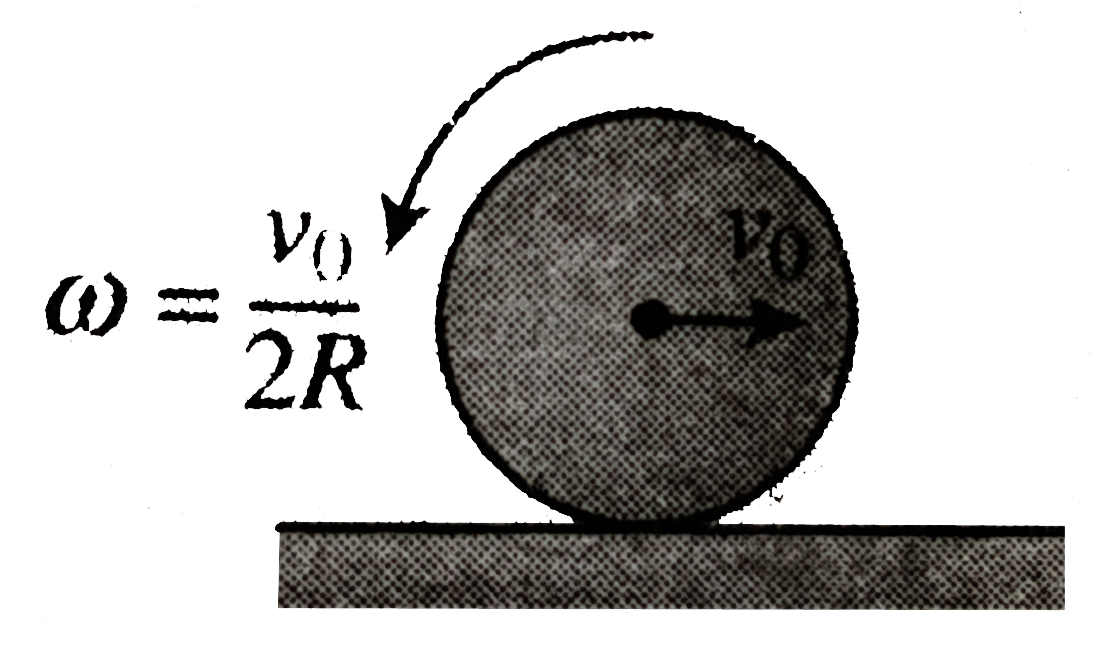
a. Because point of contact is sipping in forward direction relative to the surface kinetic friction fk will act in backward direction
fk=πmg
∴Retardation,a=fkm=μg
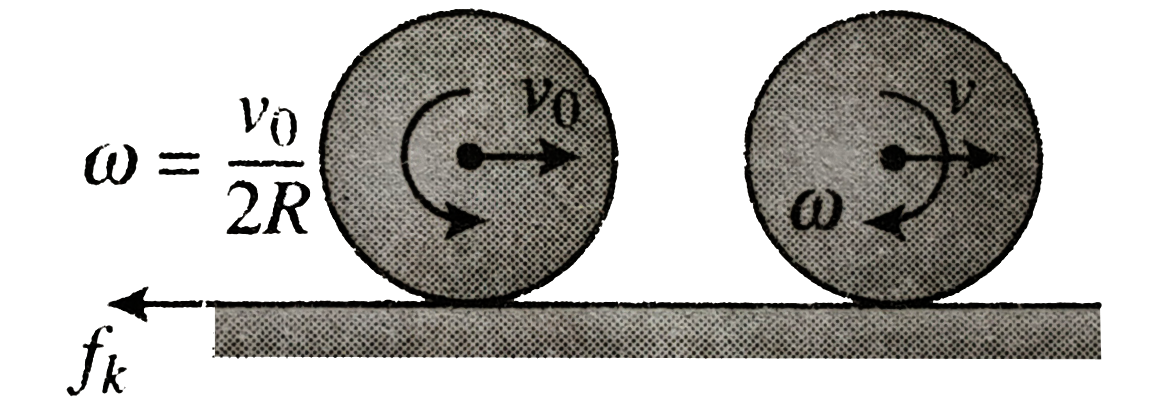
and α=fkRIcmμmgR25mR2=5μg2R
Now let when spehre starts pure rolling its velocity be v.
∴v=v0−μgt
ω−ω0+αt
v=ωR for pure rolling
v0−μ≥(−ω+αt)R
v0−μ≥(−v02R+5μ>2R)R

3v02=72μgt
∴t0=3v07μg
b. Linear speed at time t=3v07μg is
v=v0−μg(3v0)7μg=4v07
c. Friction will act till the pure rolling starts. Once the pure rolling motion starts, friction will be zero. Hence, friction does work during time interval 0<t<3v07μg and after t=3v07μg work done by friction will be zero 0<t<3v07μg work done by friction will be zero. ∵f=0
Now, work done by friction over a long time is
△Wfr=Kf−Ki
=710mv2−(12mv20+12×25mR2ω20)
=710m×16v2049−11mv2035−11mv2020
32mv20=77mv20140
△Wfr=−45mv20140=−9mv2028
Alternate method
a. Since net torque about the axis fixed to the gorund and passing through tho point of contact is zero, using conservation of angular momentum about this axis
−25mR2ω0+mv0R=25mR2ω+mvR
−15mv0R+mv0R=75mvr⇒45mv0R=75mvR
∴v=4v07
b. work done by friction △Wfr=Kf−Ki
=710mv2−1120mv20=45140mv20=−928mv20
c. Now, v=v0−μgt⇒4v07=v0−μgt
:t=3v07μg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A solid sphere is set into motion on a rough horizontal surfce with a linar speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown infigure . Find the linear speed of the sphere a. where it stops rotating and b. when slipping finally ceases sand pure rolling starts.
 View Solution
View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere is set into motion on a rough horizontal surface with a linear velocity v in the forward direction and an angular velocity v/R in the anticlockwise direction as shown in the figure. Find the linear speed of the sphere, when it stops rotating.
 Av5Bv7C3v5D3v7
Av5Bv7C3v5D3v7 - Question 2 - Select One
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct. - Question 3 - Select One
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
 View Solution
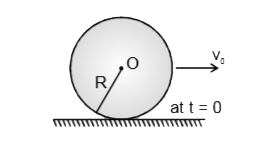
View SolutionA rigid bodyI=CMR2 is set into a motion on a rough horizontal surface with a linear speed v0 in the forward direction at time t = 0 as shown in figure. After what time slipping finally stop and pure rolling starts. Find the linear speed of the body after it starts pure rolling on the surface.
 View Solution
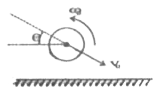
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
 View Solution
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:
 View Solution
View Solution

