A man stands on a weighing machin palced on a horizontal platform the machine reads 50kg. By mean of a suitable mechanism, the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibration per second. What will be the effect on the readin of the weighing machin? Teh amplitude of vibration of platform is 5cm. Take g=10ms−1
To solve the problem, we will analyze the effect of the harmonic vibrations on the reading of the weighing machine. The steps are as follows:
Step 1: Understand the situation
A man is standing on a weighing machine that reads 50 kg, which corresponds to a weight of W=mg=50kg×10m/s2=500N.
Step 2: Determine the frequency and amplitude of the vibrations
The platform is vibrating with a frequency of f=2Hz and an amplitude of A=5cm=0.05m.
Step 3: Calculate the angular frequency
The angular frequency ω can be calculated using the formula:
ω=2πf
Substituting the given frequency:
ω=2π×2=4πrad/s
Step 4: Calculate the maximum acceleration
The maximum acceleration amax in simple harmonic motion (SHM) is given by:
amax=ω2A
Substituting the values of ω and A:
amax=(4π)2×0.05
Calculating (4π)2:
(4π)2≈16π2≈157.91
Thus,
amax=157.91×0.05≈7.8955m/s2≈7.9m/s2
Step 5: Calculate the maximum force on the weighing machine
The maximum force Fmax on the weighing machine occurs when the platform accelerates upwards:
Fmax=mg+amax=500N+7.9N=507.9N
To convert this force back to kg:
Fmax=507.910≈50.79kg
Step 6: Calculate the minimum force on the weighing machine
The minimum force Fmin on the weighing machine occurs when the platform accelerates downwards:
Fmin=mg−amax=500N−7.9N=492.1N
To convert this force back to kg:
Fmin=492.110≈49.21kg
Step 7: Conclusion
The reading of the weighing machine will oscillate between approximately 49.21 kg and 50.79 kg due to the harmonic vibrations of the platform.
A man is standing on a weighing machine that reads 50 kg, which corresponds to a weight of W=mg=50kg×10m/s2=500N.
The platform is vibrating with a frequency of f=2Hz and an amplitude of A=5cm=0.05m.
The angular frequency ω can be calculated using the formula:
ω=2πf
Substituting the given frequency:
ω=2π×2=4πrad/s
The maximum acceleration amax in simple harmonic motion (SHM) is given by:
amax=ω2A
Substituting the values of ω and A:
amax=(4π)2×0.05
Calculating (4π)2:
(4π)2≈16π2≈157.91
Thus,
amax=157.91×0.05≈7.8955m/s2≈7.9m/s2
The maximum force Fmax on the weighing machine occurs when the platform accelerates upwards:
Fmax=mg+amax=500N+7.9N=507.9N
To convert this force back to kg:
Fmax=507.910≈50.79kg
The minimum force Fmin on the weighing machine occurs when the platform accelerates downwards:
Fmin=mg−amax=500N−7.9N=492.1N
To convert this force back to kg:
Fmin=492.110≈49.21kg
The reading of the weighing machine will oscillate between approximately 49.21 kg and 50.79 kg due to the harmonic vibrations of the platform.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - conceptual problems
84 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions
99 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - CURIOSITY QUESTION
2 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
When a man stands on a weighing machine placed on a horizontal platform, it reads 60 kg . With the help of a suitable mechanism, the platform is made to undergo vertical harmonic vibrations with a frequency of 1 vibration per second. Determine the effect of this S.H.M. on the reading of the weighing machine, The amplitude of vibration of the platform is 4 cm. Take g = 10 m/s2.
View SolutionA boy is standing on a weighing machine placed on a horizontal platform. The reading of weighing machine is 70 kg. Using a suitable mechanism the platform is made to execute harmonic vibrations with a frequency of 1 vibration per second. Calculate the maximum and minimum force exerted on the boy if the amplitude of vibration of platform is 6 cm.
View Solution
Knowledge Check
A man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2πHz. Which of the following statement is correct ?
 AThe spring balance reads the weight of man as 60kgBThe spring balance reading fluctuates between 60kg and 70kgCThe spring balance reading fluctuates bettween 50kg and 60kgDThe spring balance reading fluctuates between 50kg and 70kg
AThe spring balance reads the weight of man as 60kgBThe spring balance reading fluctuates between 60kg and 70kgCThe spring balance reading fluctuates bettween 50kg and 60kgDThe spring balance reading fluctuates between 50kg and 70kg
The bob of a simple pendulum executes simple harmonic motion with amplitude 4 cm and frequency 10 vibrations per second. Calculate the kinetic energy of the bob in lowest position if mass of bob is 2 kg.
View SolutionA horizontal platform vibrate up and down with a simple harmonic motion of amplitude 20 c.m. At what frequency will an object kept on the platform remain just in contact with the platform ? Take g=9.81m/s2.
View SolutionTwo blocks A and B having mass m = 1 kg and M = 4 kg respectively are attached to a spring and placed vertically on a weighing machine as shown in the figure. Block A is held so that the spring is relaxed. A is released from this position and it performs simple harmonic motion with angular frequency w=25rads−1. The spring remains vertical
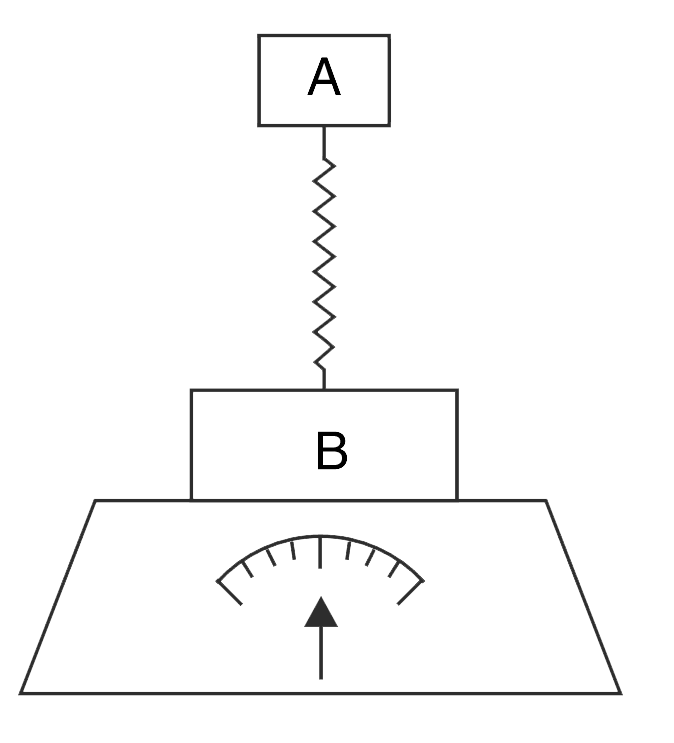
(a) Find the reading of the weighing machine as a function of time. Take t = 0 when A is released.
(b) What is the maximum reading of the weighing machine ?
View SolutionA person of mass 50kg stands on a weighting scale on a lift If the lift is ascending upwards with a uniform acceleration of 9ms^(-2) what would be the reading of the weighing scale?(g=10ms^(-1)) in kg wt
View SolutionA man is standing on a platform moving up and down as a S.H.M. will there be any change in his weight as recorded by a weighing machine on the platform ?
View SolutionA man is standing on a platform moving up and down as a S.H.M. will there be any change in his weight as recorded by a weighing machine on the platform ?
View SolutionA woman weighing 50 kgf stands on a weighing machine placed in lift. What will be the reading of the machine, when the lift is (i) moving upwards with a uniform velocity of 5ms−1 and (ii) moving downwards with a uniform acceleration of 1ms−2 ? Take g = 10 ms−2.
View Solution
