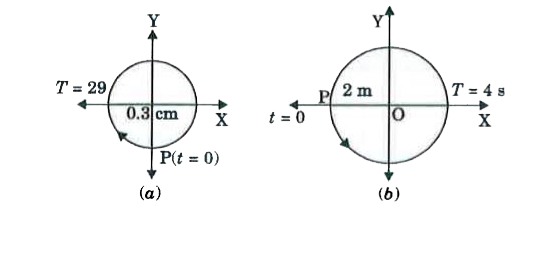
depict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
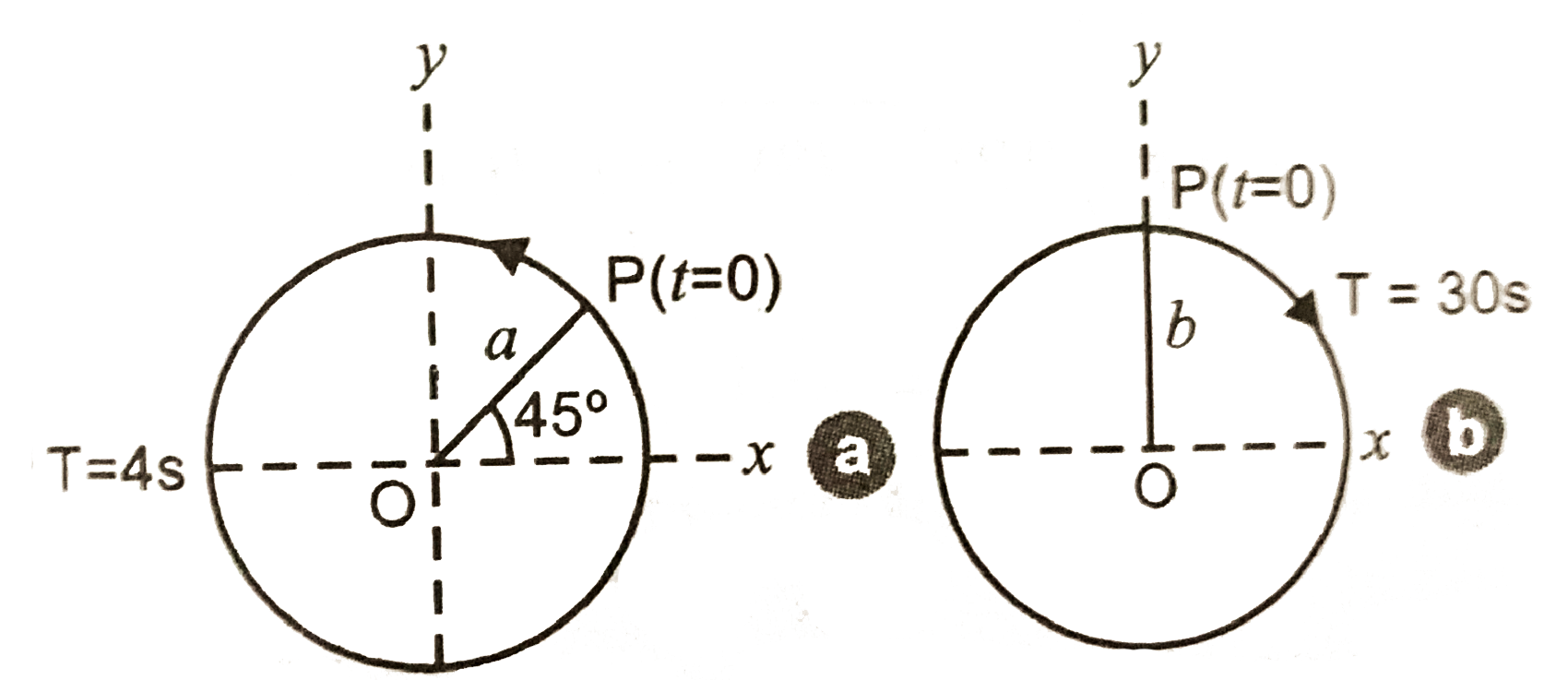
Refere to figure , T=4s, intial pahse, ϕ=45∘=π4rad with the positive direction of x-axis. After a time t, it covers an angle 2πTt in the anitclockwise direction and makes an angle (2πTt+π4) with the x-axis. The projectino of OP on the x-axis at time t is
x=acos(2pπtT+ϕ)=acos(2πt4+π4)
Refer to figure T=30s inital phase, ϕ=90∘=π2rad with the x-axis. After a time t, it covers an angle 2πtT in the clockwise direction and makes an angle (π2−2πtT) with the x-axis. Now, the projection of OP on the x-axis at time t is given by
x=bcos(π2−2πtT)=bcos(2πtT−π2)
bcos(2πt30−π2)=bcos(πt15−π2)
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - conceptual problems84videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions99videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - CURIOSITY QUESTION2videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
The following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
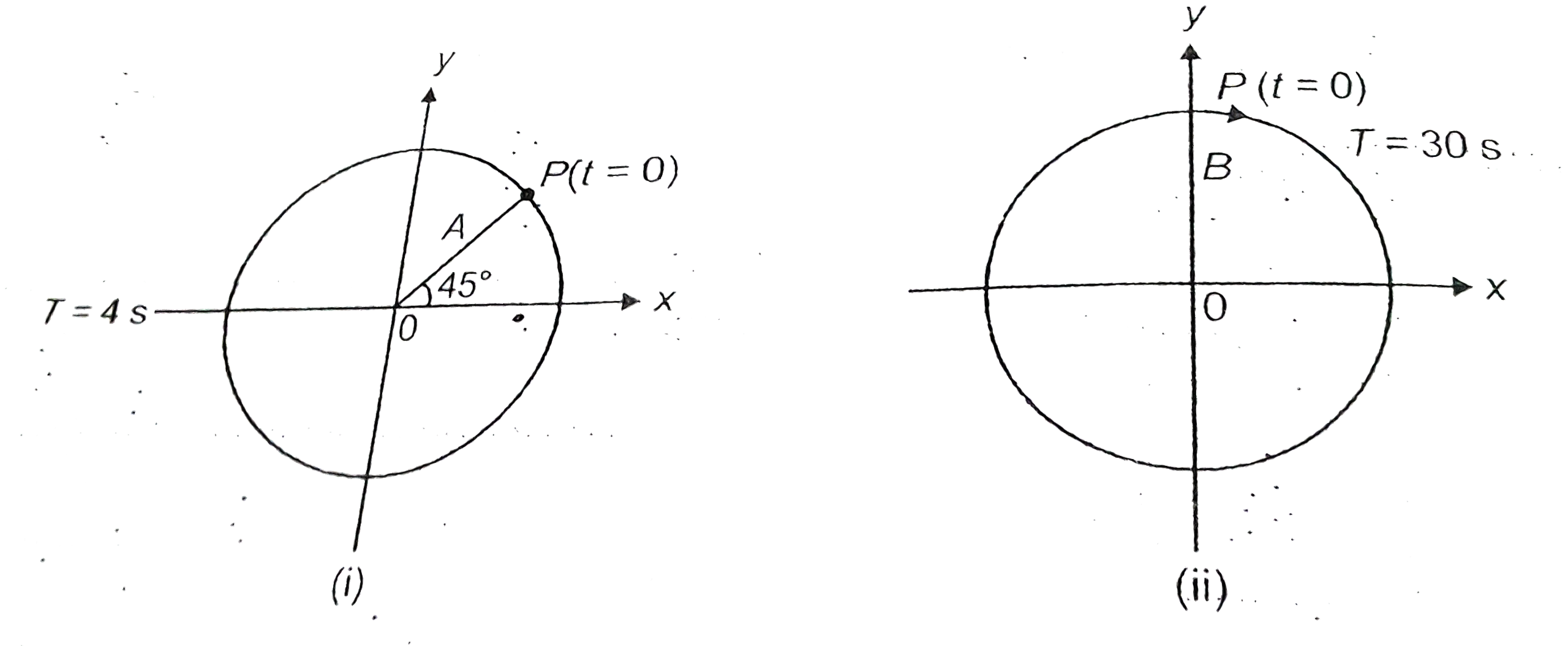 View Solution
View Solution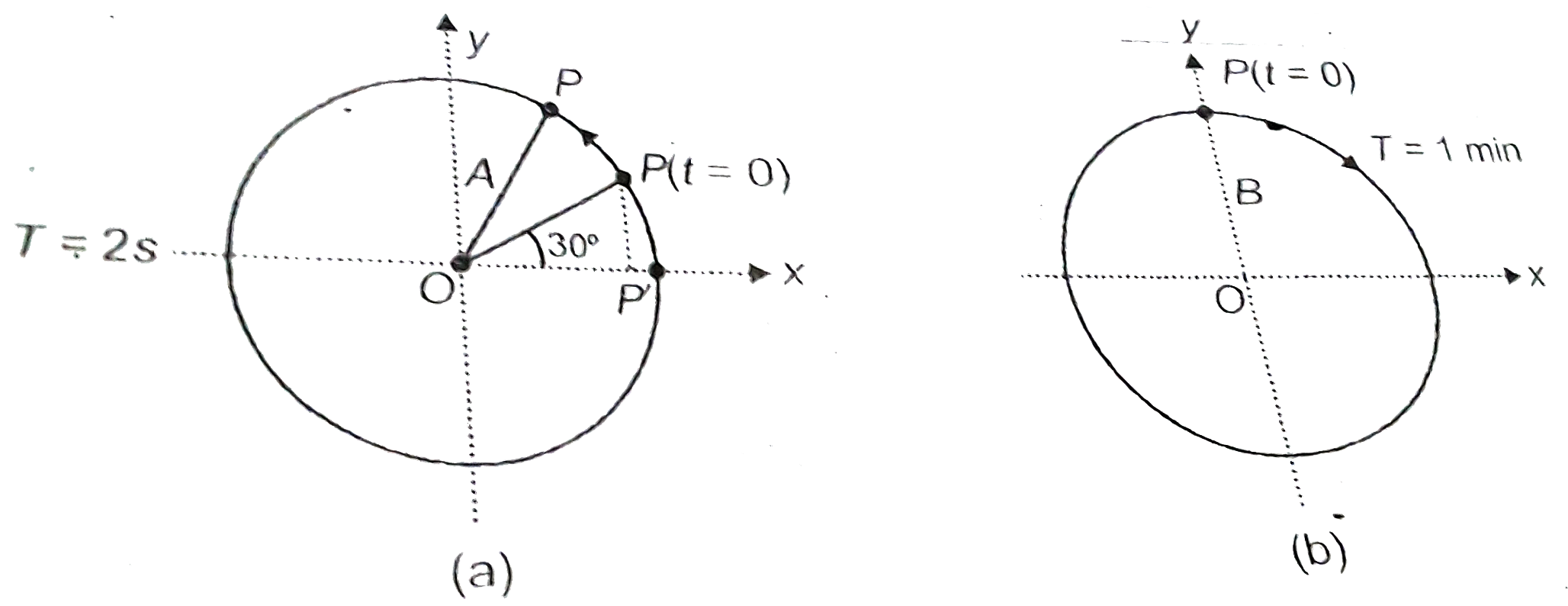
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.View Solution
Knowledge Check
- Question 1 - Select One
The following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
 Ax(t)=acos(2πt4+π4)Bx(t)=acos(πt4+π4)Cx(t)=asin(2πt4+π4)Dx(t)=acos(πt3+π2)
Ax(t)=acos(2πt4+π4)Bx(t)=acos(πt4+π4)Cx(t)=asin(2πt4+π4)Dx(t)=acos(πt3+π2) - Question 2 - Select One
the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
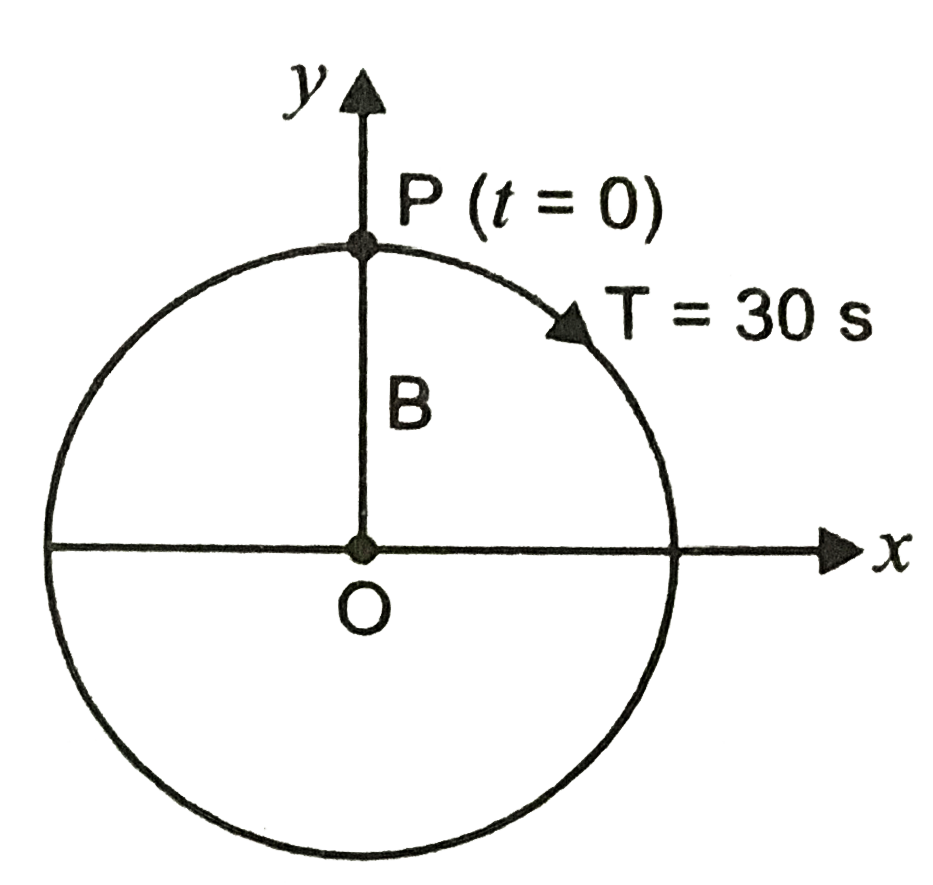 Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2) - Question 3 - Select One
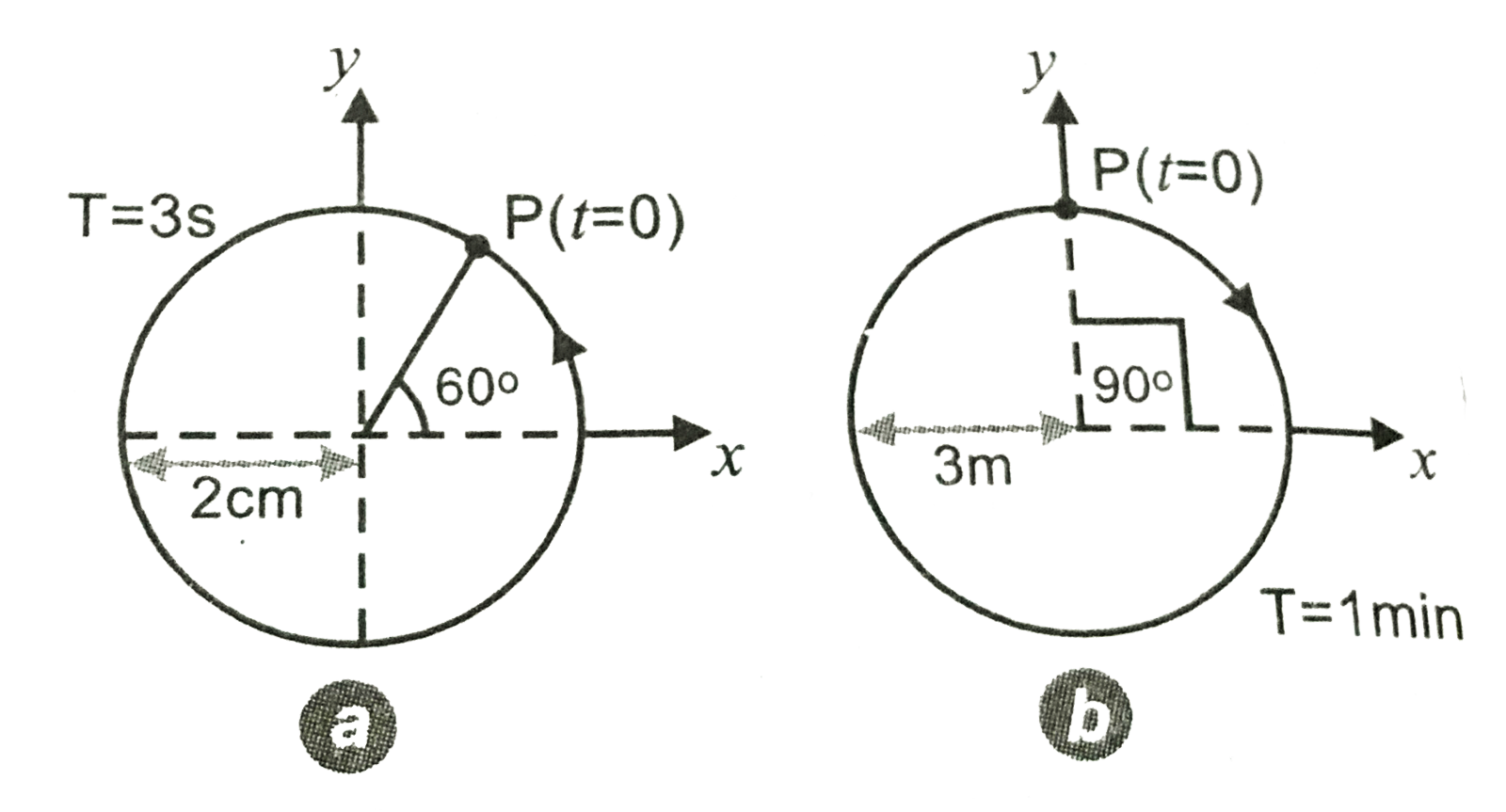
Figure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
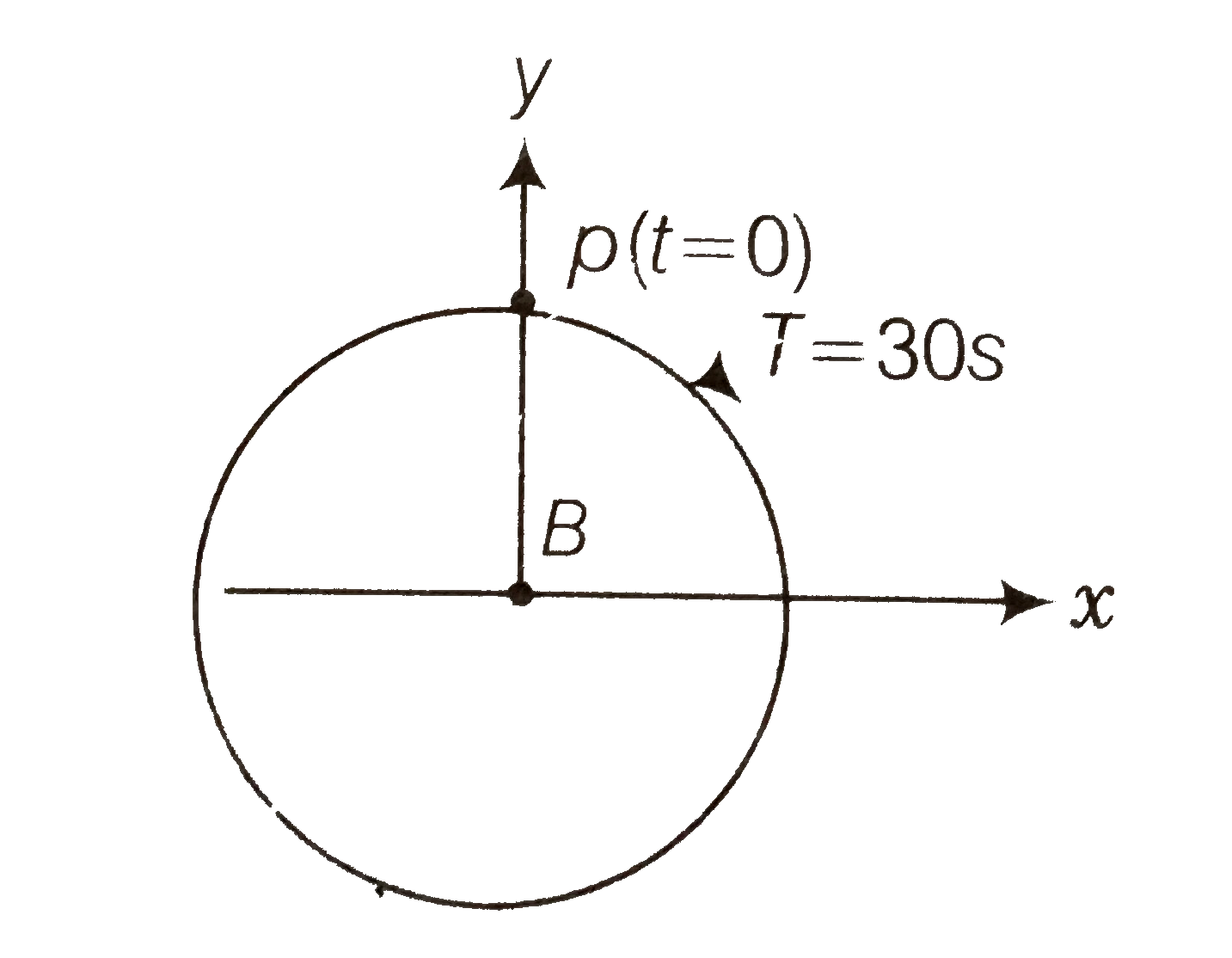 Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
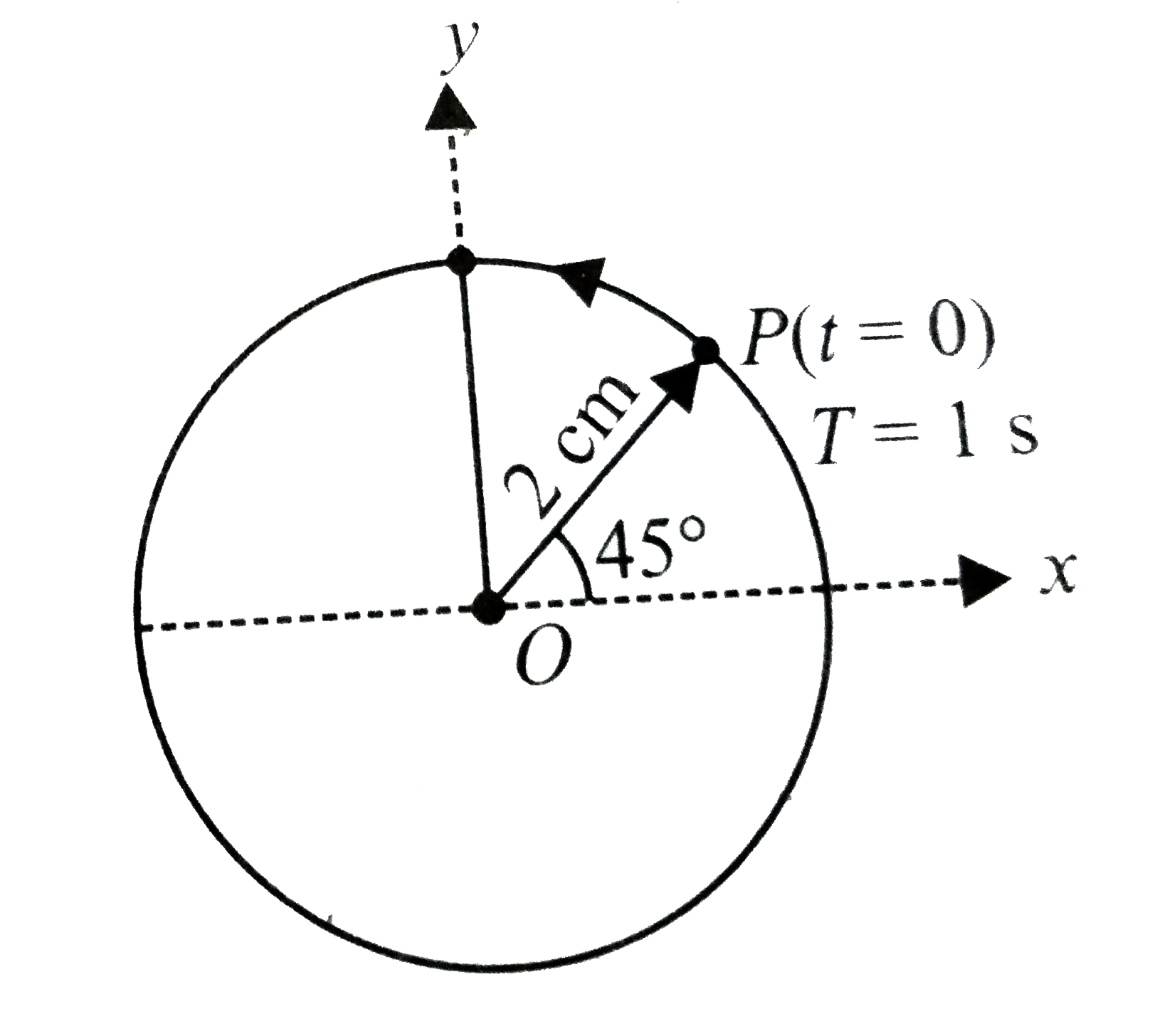
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P isView SolutionFrom the figure, obtain the equation of simple harmonic motion of the y-projection of the radius vector of the revolving particle P in each case.
 View Solution
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated in the · figure. The simple harmonic motion of the X-projection of the radius vector of the rotating particle Pis
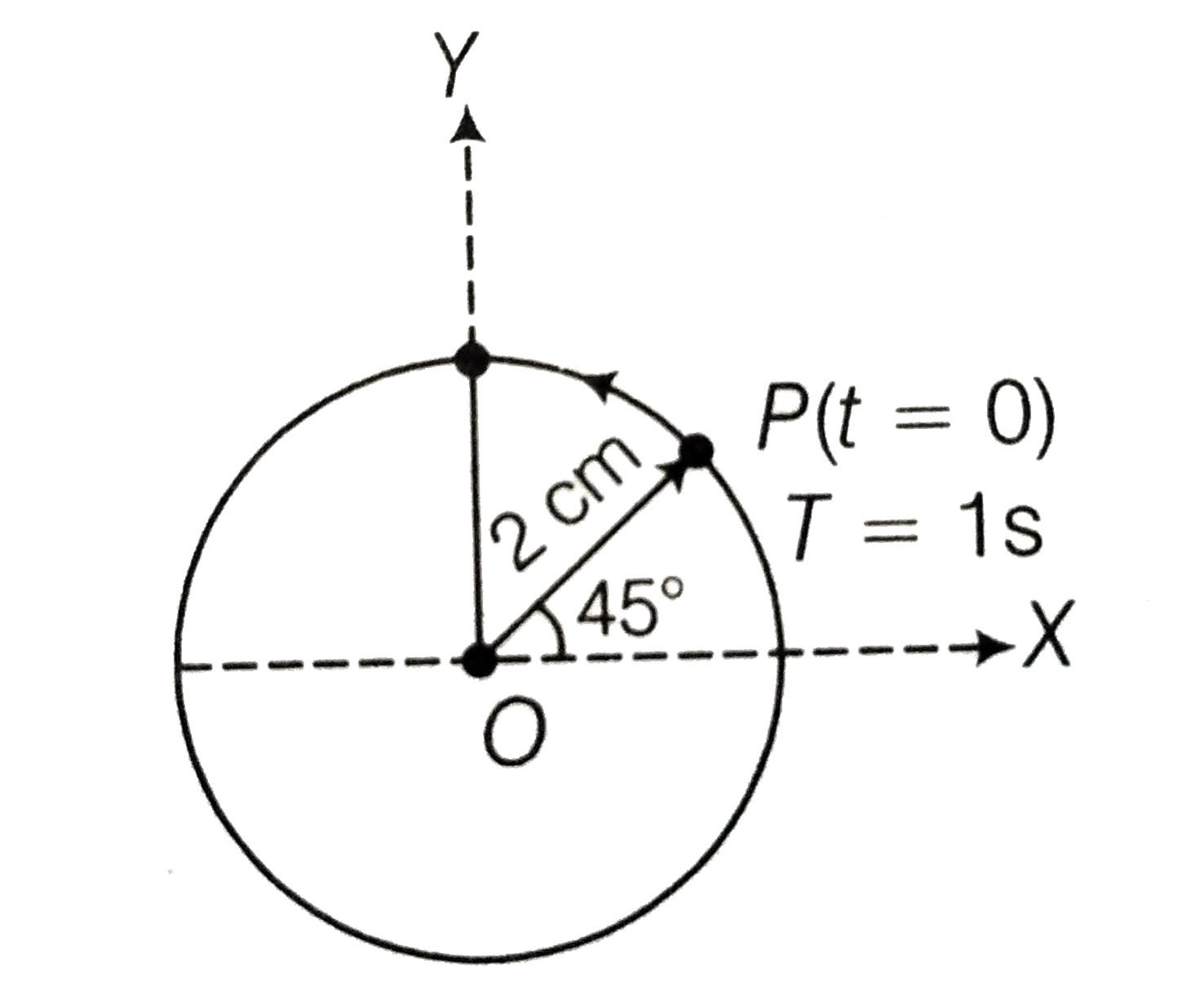 View Solution
View SolutionFigure below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
 View Solution
View SolutionThe radius of cirlcue, the period of revolution, initial position and sense of revolution are indicated in the figure.

y-projection of the radius vector of rotating particle P is :View Solution
