A man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of $50 m \times 50 m$ is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s $(v < 1)$ . What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?

Video Solution

Text Solution

Verified by Experts

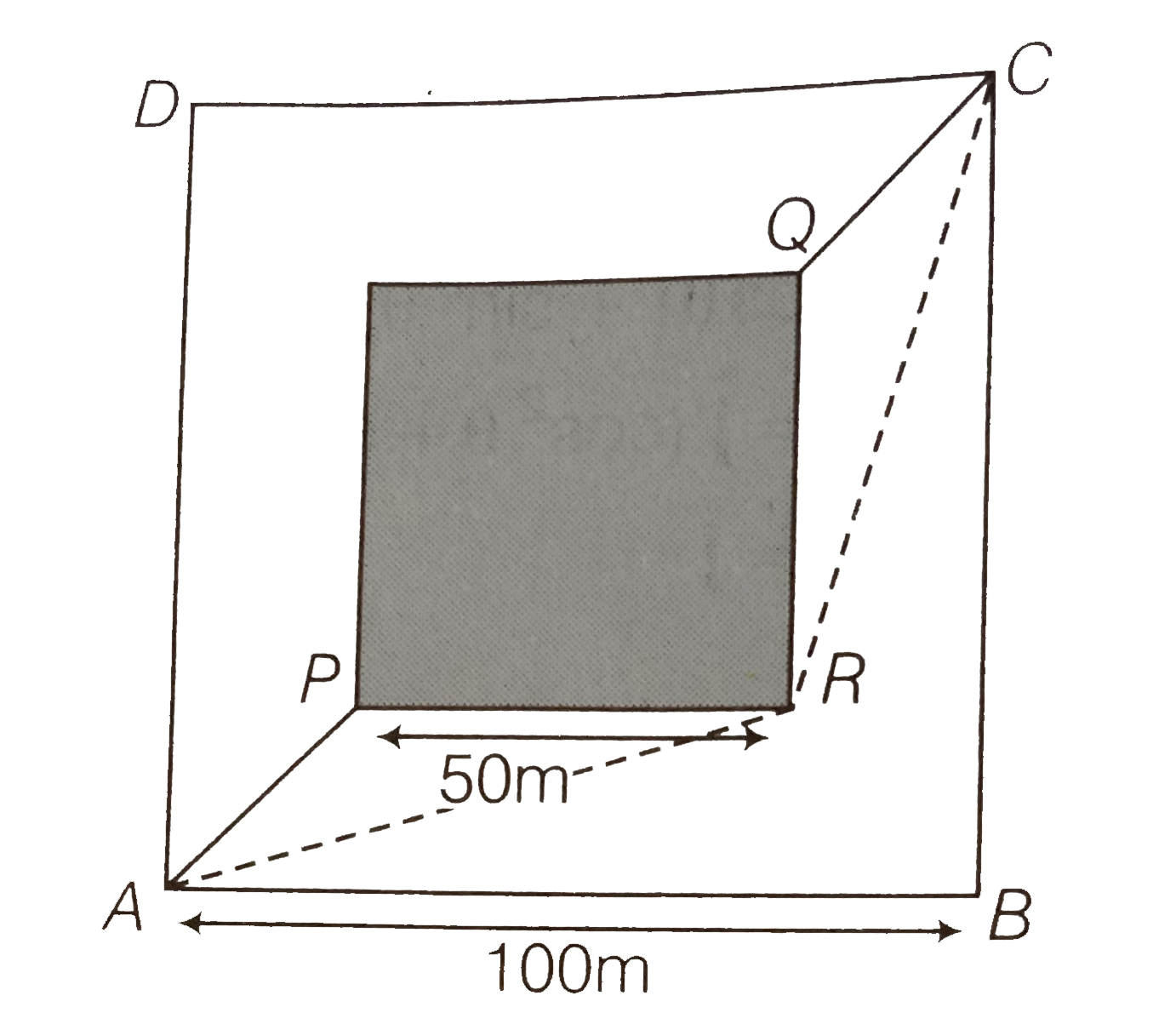
Consider adjacent diagram

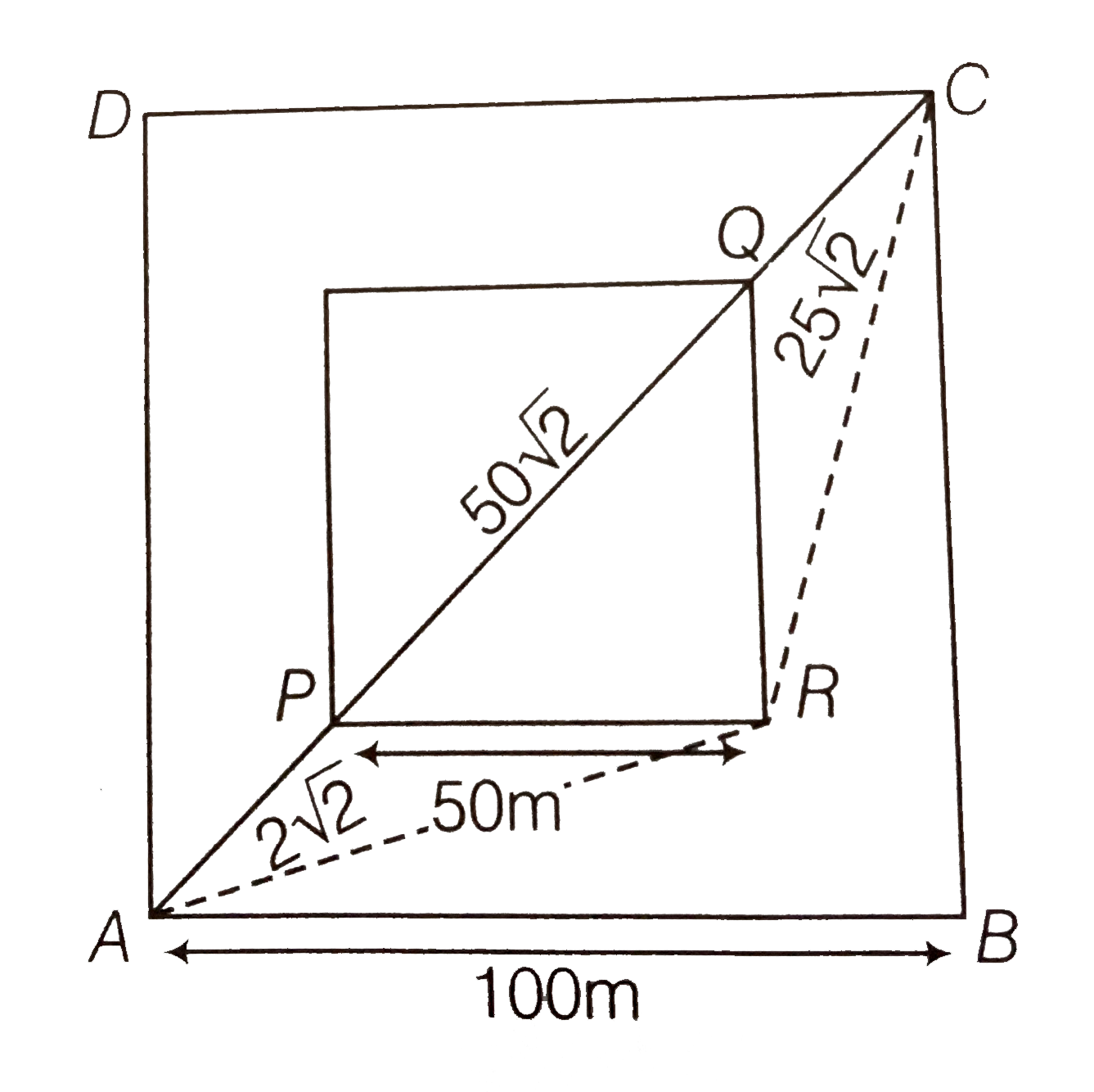
Time taken to go from A to C via straight line path APQC through the S and
$T_{sand} = \frac{A P + Q C}{1} + \frac{P Q}{v} = \frac{25 \sqrt{2} + 25 \sqrt{2}}{1} + \frac{50 \sqrt{2}}{v}$
$= 50 \sqrt{2} + 50 \frac{\sqrt{2}}{v} = 50 \sqrt{2} (\frac{1}{v} + 1)$
Clearly from figure the shortest path outside the sand will be ARC.
Time taken to go from A to C via this path
$T_{outside} = \frac{A R + R C}{1} s$
$Clearly A R = \sqrt{75^{2} + 25^{2}} = \sqrt{75 \times 75 + 25 \times 25}$
$= 5 \times 5 \sqrt{9 + 1} = 25 \sqrt{10} m$
$R C = A R = \sqrt{75^{2} + 25^{2}} = 25 \sqrt{10} m$
$\Rightarrow T_{outside} = 2 A R = 2 \times 25 \sqrt{10} s = 50 \sqrt{10} s$
$For T_{sand} < T_{outside}$
$\Rightarrow 50 \sqrt{2} (\frac{1}{v} + 1) < 2 \times 25 \sqrt{10}$
$\Rightarrow \frac{2 \sqrt{2}}{2} (\frac{1}{v} + 1) < \sqrt{10}$
$\Rightarrow \frac{1}{v} + 1 < \frac{2 \sqrt{10}}{2 \sqrt{2}} = \frac{\sqrt{5}}{2} \times 2 = \sqrt{5}$
$\Rightarrow \frac{1}{v} < \frac{\sqrt{5}}{2} \times 2 - 1 \Rightarrow \frac{1}{v} < \sqrt{5} - 1$
$\Rightarrow v < \frac{1}{\sqrt{5} - 1} \approx 0.81 m / s$
$\Rightarrow v < 0.81 m / s$

Updated on:21/07/2023

|

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

IF the area of square is $25 m^{2}$ , then the side of the square is
A125
B625
C $\frac{1}{25}$
D5
The side of a square park is 100 m. Perimeter of the park is:
A1000 m
B400 m
C200 m
D800 m

NCERT EXEMPLAR-MOTION IN A PLANE-Multiple Choice Questions

Home
Ask Doubt
Profile