The young's modulus for steel is much more then that for rubber. For the same longitudinal strain, which one will have greater tensil stress ?
Young's modulus (Y) = StressLongitudinal strain
For same longitudinal strain, Y ∝ stress
∴ YsteelYrubber=(stress)steel(stress)rubber ....(i)
But Ysteel>Yrubber
∴ YsteelYrubber>1
Therefore, from Eq. (i),
(stress)steel(stress)rubber>1
⇒ (stress)steel>(stress)rubber
Topper's Solved these Questions
Similar Questions
Which one is more elastic rubber or steel? Explain.
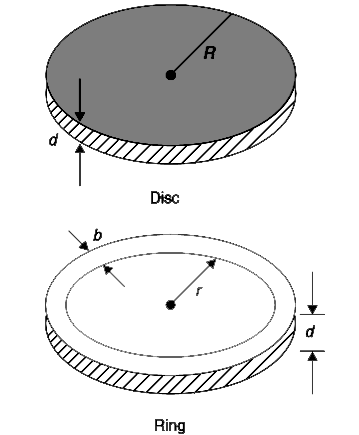
View SolutionA steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take b<<r]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The ratio of tensile stress to the longitudinal strain is defined as
AÂ bulk modulusBYoung's modulusCshear modulusDcompressibility - Question 2 - Select One
The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
A1:1B1:2C2:1D4:1 - Question 3 - Select One
The Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
A1:1B1:2C2:1D4:2
Young's modulus of material of the rod is 24 times 1010Pa When the longitudinal strain is 0.01% then energy stored per unit volume of the rod is
View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View SolutionA steel sphere and a wooden sphere have the same mass. Then which will have greater moment of inertia about the diameter ?
View SolutionThe young’s modulus of a wire is numerically equal to the stress which wire
View SolutionTwo wire of same radius and lengh the are subjected to the same load. One wire is of steel and the other is of copper. If the Young's modulus of steel is twice that of copper, the ratio the energy stored per unit volume in steel to that of copper wire is
View Solution

