A cricket fielder can throw the cricket ball with a speed $v_{0}$ . If he throws the ball while running with speed (u) at angle $θ$ to the horizontal, find
(b) what will be time of flight ?
(c ) what is the distance (horizontal range) form the point of projection at which the ball will land ?
(d) find $θ$ at which he should throw the ball that would maxmise the horizontal range range as found in (c ).
(e) how does $θ$ for maximum range change if $u > v_{0}, u = v_{0}, t - v_{0}$ ?
(f) how does $θ$ in (e) compare with that for u=0 (i.e., 45^@) ?

Video Solution

Text Solution

Verified by Experts

Consider the adjacent diagram.

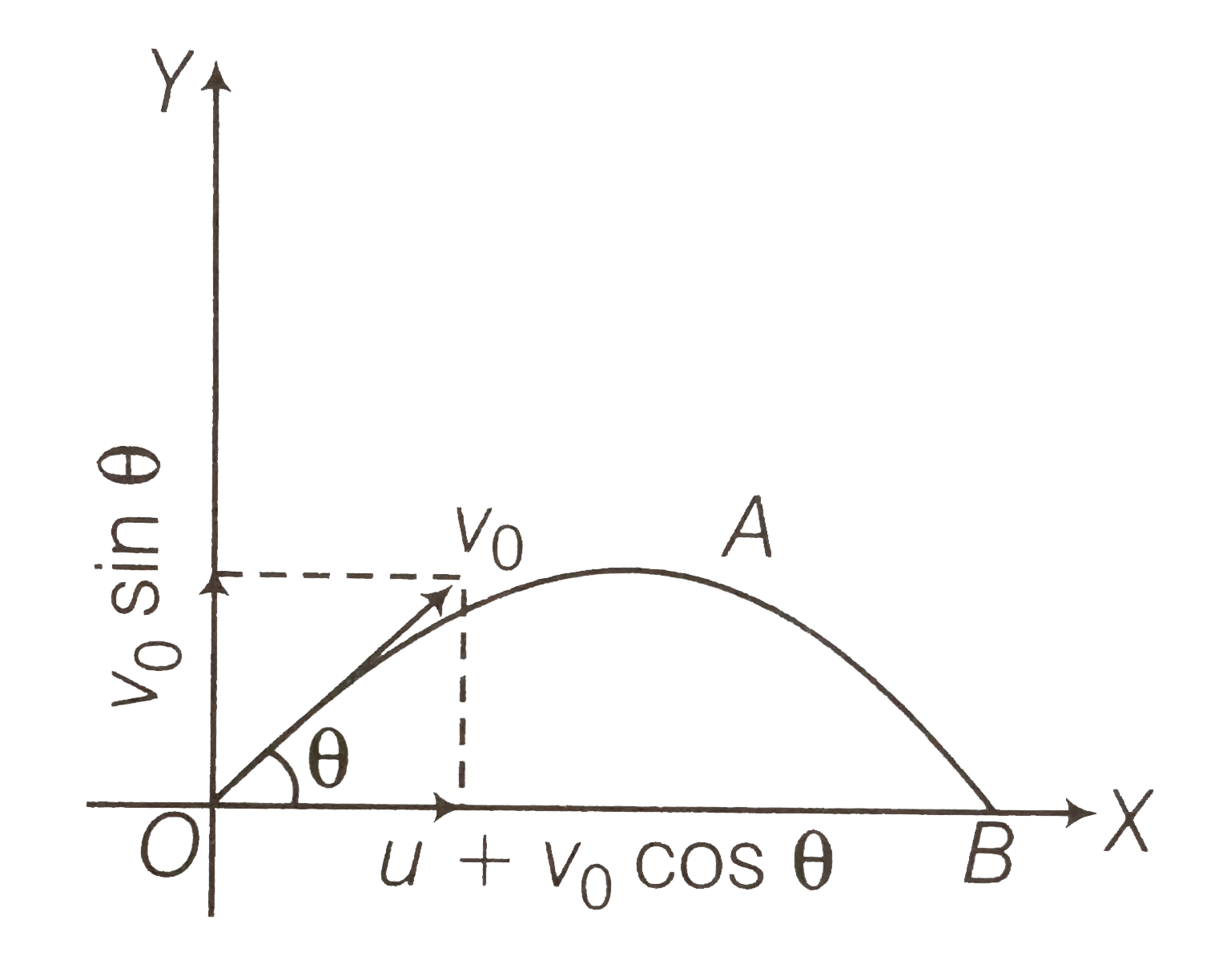
(a) Initial velocity in
x-direction , $u_{x} = u + v_{0} cos θ$
$u_{y}$ =Initial velocity in Y - direction
$= v_{0} sin θ$
where angle of projection is $θ$ .
Now, we can write
$tan θ = \frac{u_{y}}{u_{x}} = \frac{u_{0} sin θ}{u + u_{0} cos θ}$
$\Rightarrow θ = {tan}^{- 1} (\frac{v_{0} sin θ}{u + v_{0} cos θ})$
(b) Let T be the time of flight.
As net displacement is zero over time period T.
$y = 0, u_{y} = v_{0} sin θ, a_{y} = - g, t = T$
We know that $y = u_{y} t + \frac{1}{2} a_{y} t^{2}$
$\Rightarrow 0 = v_{0} sin θ T + \frac{1}{2} (- g) T^{2}$
$\Rightarrow T [v_{0} sin θ - \frac{g}{2} T] = 0 \Rightarrow T = 0, \frac{2 v_{0} sin θ}{g}$
$T = 0_{1}$ , corresponds to point O.
Hence, $T = \frac{2 u_{0} sin θ}{g}$
(c) Horizontal range , $R = (u + v_{0} cos θ) T = (u + v_{0} cos θ) \frac{2 v_{0} sin θ}{g}$
$= \frac{v_{0}}{g} [2 u sin θ + v_{0} sin 2 θ]$
(d) For horizontal range to be maximum, $\frac{d R}{d θ} = 0$
$\Rightarrow \frac{v_{0}}{g} [2 u cos θ + v_{0} cos 2 θ \times 2] = 0$
$\Rightarrow 2 u cos θ + 2 v_{0} [2 {cos}^{2} θ - 1] = 0$
$\Rightarrow 4 v_{0} {cos}^{2} θ + 2 u cos θ - 2 v_{0} = 0$
$\Rightarrow 2 v_{0} {cos}^{2} θ + u cos θ - v_{0} = 0$
$\Rightarrow cos θ = \frac{- u \pm \sqrt{u^{2} + 8 v_{0}^{2}}}{4 v_{0}}$
$\Rightarrow θ_{max} = {cos}^{- 1} ⎡ ⎢ ⎢ ⎣ \frac{- u \pm \sqrt{u^{2} + 8 v_{0}^{2}}}{4 v_{0}} ⎤ ⎥ ⎥ ⎦$
$= {cos}^{- 1} ⎡ ⎢ ⎢ ⎣ \frac{- u \pm \sqrt{u^{2} + 8 v_{0}^{2}}}{4 v_{0}} ⎤ ⎥ ⎥ ⎦$
(e) If $u = v_{0}$ ,
$cos θ = \frac{- v_{0} \pm \sqrt{v_{0}^{2} + 8 v_{0}^{2}}}{4 v_{0}} = \frac{- 1 + 3}{4} = \frac{1}{2}$
$\Rightarrow θ = 60^{\circ}$
$If u < < v_{0}, then 8 v_{0}^{2} + u^{2} \approx 8 v_{0}^{2}$
$θ_{max} = {cos}^{- 1} [\frac{- u \pm 2 \sqrt{2} v_{0}}{4 v_{0}}] = {cos}^{- 1} [\frac{1}{\sqrt{2}} - \frac{u}{4 v_{0}}]$
$If u < < v_{0}, then θ_{max} = {cos}^{- 1} (\frac{1}{\sqrt{2}}) = \frac{π}{4}$
$If u > u_{0} and u > > v_{0}$
$θ_{max} = {cos}^{- 1} [\frac{- u \pm u}{4 v_{0}}] = 0 \Rightarrow θ_{max} = \frac{π}{2}$
(f) $If u = 0, θ_{max} = {cos}^{- 1} [\frac{0 \pm \sqrt{8 v^{2} 0}}{4 v_{0}}] = {cos}^{- 1} (\frac{1}{\sqrt{2}}) = 45^{\circ}$

Updated on:21/07/2023

A cricket fielder can throw the cricket ball with a speed $v_{0}$ .If the throws the ball while running with speed $u$ at an angle $θ$ to the horizontal.
The effective angle to the horizontal at which the ball is projected in air as seen by a spector is
A $θ = {tan}^{- 1} (\frac{v_{0} sin θ}{u + v_{0} cos θ})$
B $θ = {tan}^{- 1} (\frac{v_{0} cos θ}{u + v_{0} sin θ})$
C $θ = {cot}^{- 1} (\frac{v_{0} cos θ}{u + v_{0} sin θ})$
D $θ = {cot}^{- 1} (\frac{v_{0} cos θ}{u + v_{0} sin θ})$
A particle is projected with speed $u$ at angle $θ$ to the horizontal. Find the radius of curvature at highest point of its trajectory
A $\frac{u^{2} {cos}^{2} θ}{2 g}$
B $\frac{\sqrt{3} u^{2} {cos}^{2} θ}{2 g}$
C $\frac{u^{2} {cos}^{2} θ}{g}$
D $\frac{\sqrt{3} u^{2} {cos}^{2} θ}{g}$
A ball is projected from the ground at angle $θ$ with the horizontal. After $1 s$ , it is moving at angle $45^{\circ}$ with the horizontal and after $2 s$ it is moving horizontally. What is the velocity of projection of the ball ?
A $10 \sqrt{3} m s^{- 1}$
B $20 \sqrt{3} m s^{- 1}$
C $10 \sqrt{5} m s^{- 1}$
D $20 \sqrt{2} m s^{- 1}$