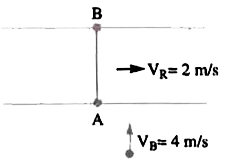
A man wishes to row across a river flowing to the right with speed of 2m/s. If they velocity that the boat can have VB=4m/s , how should the man row so as to reach across in .
(a) shortest path (b) shortest time .
(a) Shortest Path .
If the main has to move along the shortest path , then the path of this boat should be AB ( perpepndicular to river).
If the man rows vertically , the river will carry him to right , hence the man should incline his boat to the left. When his velocity is inclined , it has two components , Vx and Vy [compare with inclined velocity of cat].
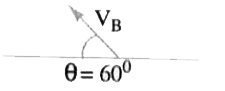
The horizontal component Vx should cancel the speed the river .
Thus Vx=VBcosθ=VR
∴4cosθ=2,θ=60∘
Alternatively , we can use resultant vertical as in cat mouse problem (Method 3).
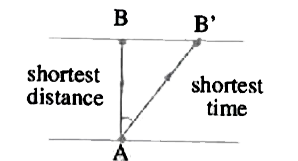
(b) Shortest time :
Note that when the man rows along shortest distance , he DOES NOT cross the river in the shortest time , because time taken to cross the river =widthe of riververtical velocity
As long as the boat is inclined at angle θ , vertical velocity is VB . To row in shortest time , the enitre velocity of boat should be used in vertical direction i.e., Man should row perpendicular to stream .
Note : When the man rows in shortest time , he does not reach point B but instead point B. Shortest distance is analogus to reaching a point on opposite bank (say house ) where shortest time is linked with only reaching opposite bank.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - LONG ANSWER TYPE QUESTIONS5videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - SHORT ANSWER TYPE QUESTIONS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)5videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
Similar Questions
A river is flowing from west to east with a speed of 5m/min. A man can swim in still water with a velocity 10m/min. In which direction should the man swim so as to take the shortest possible path to go to the south.
View SolutionA boat is rowed across a river at the rate of 4.5kmhr. The river flows at the rate of 6kmhr. The velocity of boat in ms is:
View SolutionA river is flowing from west to east at a speed of 5m/s. A man on the south bank of the river capable of swimming at 10m/s in a still water wants to swim, across the river in a shortest time. He should swim in a direction
View SolutionA man wishes to swim across a river 40 m wide flowing with a speed of 3m/s. such that he reaches the point just infront on the other bank in time not greater than 10s. The angle made by the direction he swims and river flow direction is :-
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
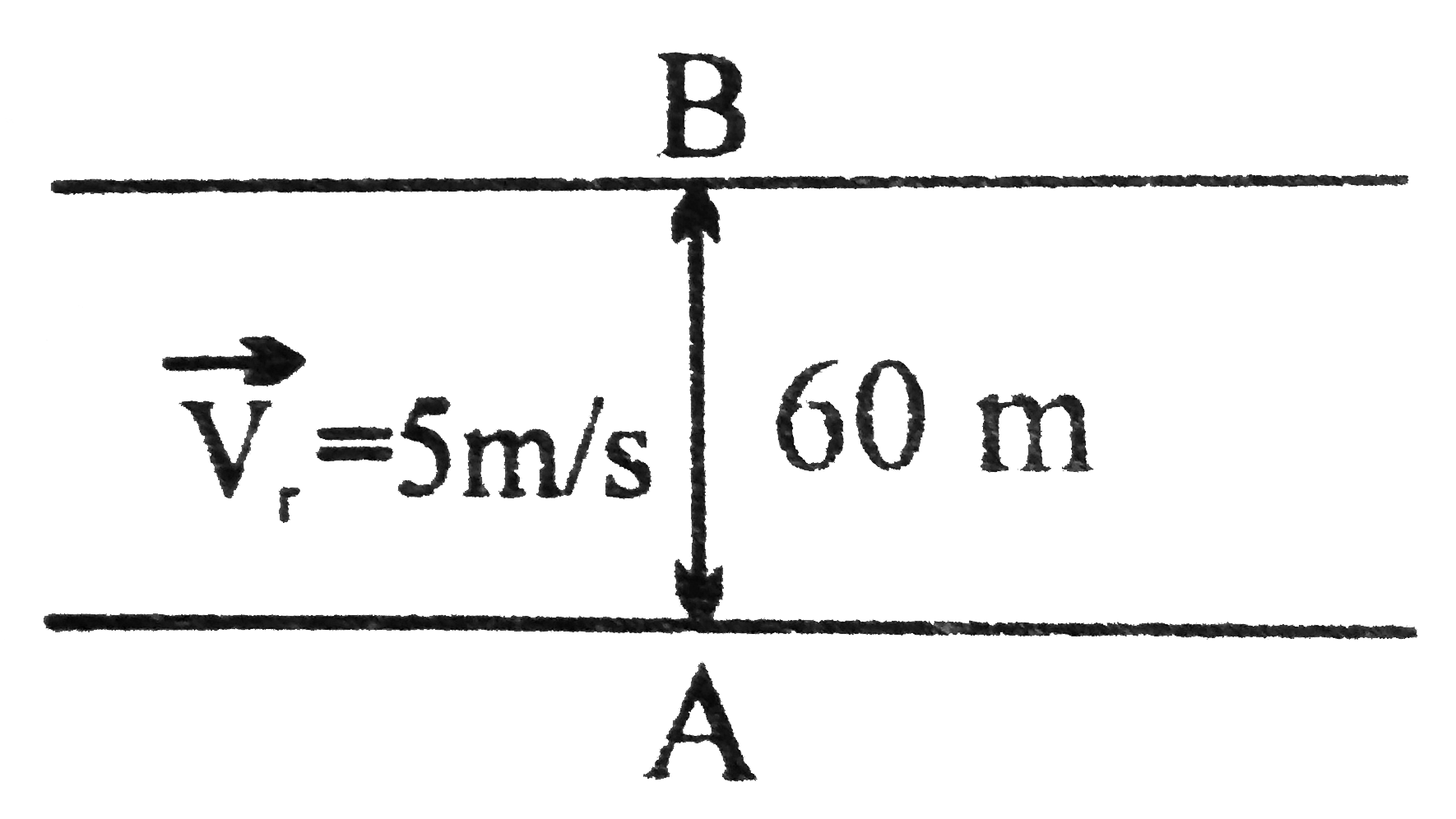
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
 View Solution
View SolutionA swimmer wishes to cross a 500m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionIn the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).
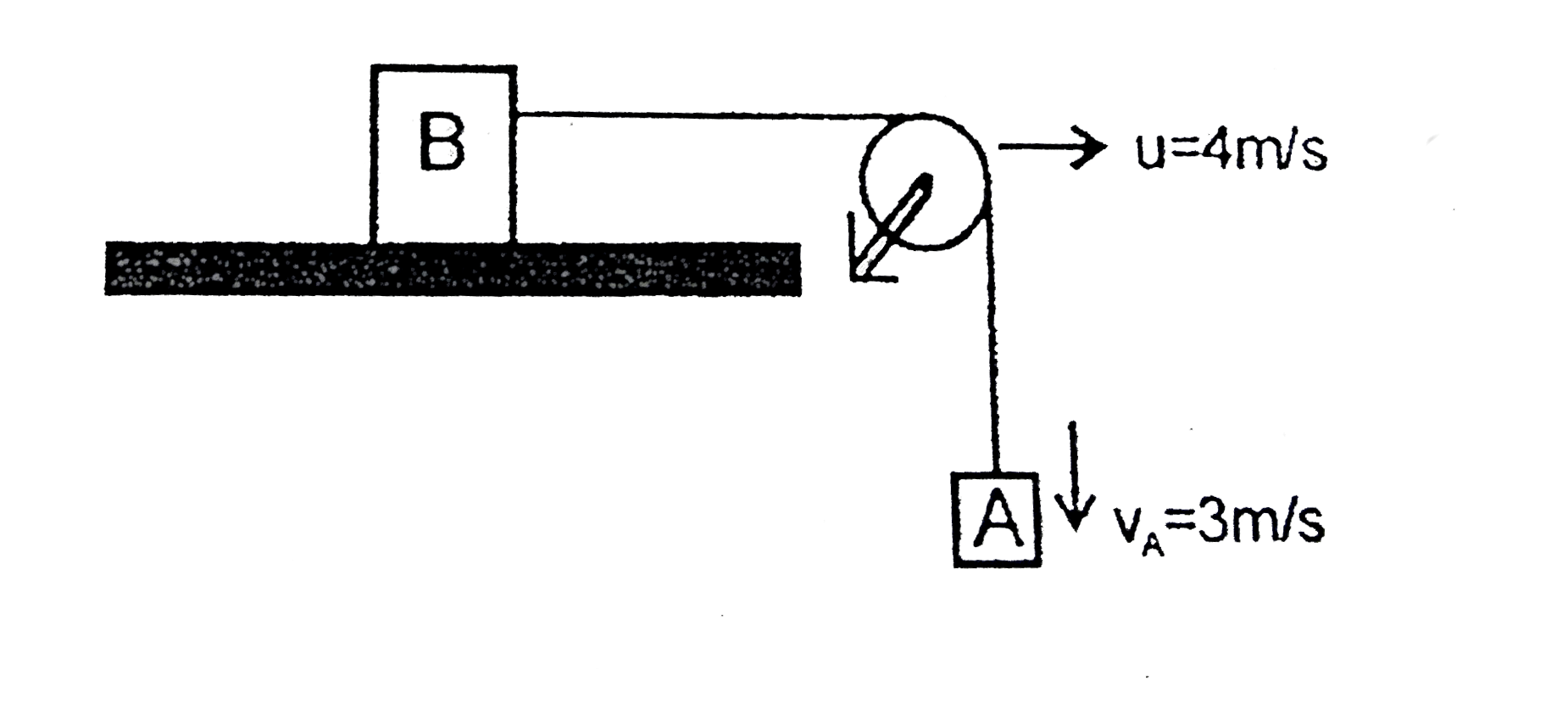 View Solution
View SolutionThe velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View Solution
